Статистическая интерпретация волн де Бройля.
Во́лны де Бро́йля — волны, связанные с любыми микрочастицами и отражающие их волновую природу. М. Борном (Макс Борн, немецкий физик-теоретик, 1882–1970, Нобелевская премия 1954 г. за статистическую интерпретацию волновой функции) была предложена статистическая интерпретация волн де Бройля. Волны де Бройля следует рассматривать как волны вероятности: Интенсивность волн де Бройля в данный момент времени и в данном месте определяет вероятность обнаружить частицу в данное время и в данном месте. А интенсивность волн пропорциональна квадрату амплитуды.
Различие между классической и квантовой физикой в определении положения и импульса частицы.
В классической механике можно определить положение и импульс движущейся точки на ее траектории в любой последовательный момент времени, если известны силы, действующие на нее.
В квантовой физике, частица не может быть описана как классическая частица, то есть например у нее не могут быть одновременно точно измерено положение и скорость (импульс). Принцип неопределённости уже в виде, первоначально предложенном Гейзенбергом, применим и в случае, когда ни одна из двух крайних ситуаций (полностью определенный импульс и полностью неопределенная пространственная координата - или полностью неопределенный импульс и полностью определенная координата) не реализуется.
Невозможность одновременного точного определения координаты и импульса частиц является следствием ограниченной точности измерительных приборов или является результатом проявления фундаментальных закономерностей?
Микрочастица, обладая и волновыми свойствами, является как бы протяженным объектом и не может одновременно иметь определенную координату и импульс, то есть нельзя утверждать, что микрочастица занимает определенное положение, и обладает определенным импульсом. Это особенность поведения микрочастицы. Иными словами, невозможно предсказать поведение каждого атома (как состоящего из этих частиц), а можно вычислить лишь среднее значение экспериментально наблюдаемых величин.
Этот принцип является фундаментальным, определяющим границы применимости классических представлений при описании свойств микромира.
34. Мысленный опыт по дифракции электронов на экран от одной щели (графическая схема эксперимента, её физико-геометричекий анализ).
Рассмотрим, например, дифракцию электронов на одиночной щели ширины D (рис. 8.4.3).
Более 85 % всех электронов, прошедших через щель, попадут в центральный дифракционный максимум. Угловая полуширина θ1 этого максимума находится из условия
| D sin θ1 = λ. |
Это формула волновой теории. С корпускулярной точки зрения можно считать, что при пролете через щель электрон приобретает дополнительный импульс в перпендикулярном направлении. Пренебрегая 15 % электронов, которые попадают на фотопластинку за пределами центрального максимума, можно считать, что максимальное значение py поперечного импульса равно

|
где p – модуль полного импульса электрона, равный, согласно де Бройлю, h / λ. Величина p при прохождении электрона через щель не меняется, т. к. остается неизменной длина волны λ. Из этих соотношений следует
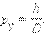
|
Прохождение электронов через щель является экспериментом, в котором y – координата электрона – определяется с точностью Δy = D. Величину Δy называют неопределенностью измерения координаты. В то же время точность определения y – составляющей импульса электрона в момент прохождения через щель – равна py или даже больше, если учесть побочные максимумы дифракционной картины. Эту величину называют неопределенностью проекции импульса и обозначают Δpy. Таким образом, величины Δy и Δpy связаны соотношением
|
которое называется соотношением неопределенностей Гейзенберга. Величины Δy и Δpy нужно понимать в том смысле, что микрочастицы в принципе не имеют одновременно точного значения координаты и соответствующей проекции импульса. Соотношение неопределенностей не связано с несовершенством применяемых приборов для одновременного измерения координаты и импульса микрочастицы. Оно является проявлением двойственной корпускулярно-волновой природы материальных микрообъектов. Соотношение неопределенностей позволяет оценить, в какой мере можно применять к микрочастицам понятия классической механики. Оно показывает, в частности, что к микрообъектам неприменимо классическое понятие траектории, так как движение по траектории характеризуется в любой момент времени определенными значениями координат и скорости. Принципиально невозможно указать траекторию, по которой двигался какой-то конкретный электрон после прохождения щели и до фотопластинки в рассмотренном мысленном эксперименте.
35. Принцип неопределенностей (Гейзенберг)
В классической механике можно определить положение и импульс движущейся точки на ее траектории в любой последо-вательный момент времени, если известны силы, действующие на нее.
Микрочастица, обладая и волновыми свойствами, является как бы протяженным объектом и не может одновременно иметь определенную координату и импульс, то есть нельзя утверждать, что микрочастица занимает определенное положение, и обладает определенным импульсом. Это особенность поведения микрочастицы. Иными словами, невозможно предсказать поведение каждого атома (как состоящего из этих частиц), а можно вычислить лишь среднее значение экспериментально наблюдаемых величин.
Этот принцип является фундаментальным, определяющим границы применимости классических представлений при опи-сании свойств микромира.
Принцип неопределенности: неопределенность значения координаты x * неопределенность скорости > h/m,математическое выражение которого называется соотношением неопределенностей Гейзенберга:
Δx* х* Δv > h/m
где Δx — неопределенность (погрешность измерения) пространственной координаты микрочастицы, Δv — неопределенность скорости частицы, m — масса частицы, а h — постоянная Планка, названная так в честь немецкого физика Макса Планка, еще одного из основоположников квантовой механики. Постоянная Планка равняется примерно 6,626 x 10–34 Дж·с, то есть содержит 33 нуля до первой значимой цифры после запятой.
36.  Соотношения неопределённостей
Соотношения неопределённостей
Соотношения неопределённостей – фундаментальные соотношения квантовой механики, устанавливающие предел точности одновременного определения так называемых дополнительных физических величин, характеризующих систему (например, координаты и импульса). В упрощённой формулировке эти соотношения утверждают, что дополнительные физические величины не могут быть одновременно точно определены. Неопределённостей соотношения являются следствием двойственной, корпускулярно-волновой природы частиц материи, отражением вероятностной (статистической) сути квантовой механики.
Неопределённостей соотношения имеют вид неравенств, например,  x
x  p >
p > 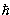 = h/2
= h/2 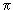 , где
, где  x – неопределённость координаты (частицы или системы),
x – неопределённость координаты (частицы или системы),  p – неопределённость её импульса, а h = 6.6.10-34 Дж.с = 4.1.10-15 эВ.с - постоянная Планка. Отсюда видно, что произведение неопределённостей координаты и импульса не может быть меньше
p – неопределённость её импульса, а h = 6.6.10-34 Дж.с = 4.1.10-15 эВ.с - постоянная Планка. Отсюда видно, что произведение неопределённостей координаты и импульса не может быть меньше 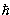 , и никаким усовершенствованием методов наблюдения нельзя преодолеть этот рубеж. Увеличение точности определения координаты неизбежно ведёт к потере точности определения импульса. Предельная точность одновременного определения координаты и импульса даётся соотношением
, и никаким усовершенствованием методов наблюдения нельзя преодолеть этот рубеж. Увеличение точности определения координаты неизбежно ведёт к потере точности определения импульса. Предельная точность одновременного определения координаты и импульса даётся соотношением  x·
x·  p
p 
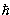 . также см вопрос 34
. также см вопрос 34
37. Физический смысл соотношений неопределённостей.
Непосредственно из преобразований Лоренца получены соотношения ΔpxΔx ≥ H и ΔEΔt ≥ H. Первое связывает неопределенность Δpx проекции px импульса рассмотренного объекта с неопределенностью Δx координаты x, а второе – неопределенность ΔE энергии E объекта с неопределенностью Δt момента t наблюдения. Величина H в соотношениях обладает размерностью действия и зависит от точности часов стержня и его массы.
38. Какой смысл имеют величины, входящие в формулу DЕ × Dt ³ h
Другая важная пара дополнительных физических величин – энергия Е и время t. Соотношение неопределённостей для них имеет вид  Е·
Е·  t >
t > 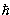 . Это соотношение для релятивистских системы или частиц (двигающихся со скоростью близкой к скорости света с) может быть получено из соотношения неопределённостей для координаты и импульса простым преобразованием:
. Это соотношение для релятивистских системы или частиц (двигающихся со скоростью близкой к скорости света с) может быть получено из соотношения неопределённостей для координаты и импульса простым преобразованием:  x/с·
x/с·  pс =
pс =  t
t  Е >
Е > 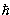 . Полученное соотношение для времени и энергии можно трактовать следующим образом. Для того, чтобы определить энергию частицы (системы) с точностью
. Полученное соотношение для времени и энергии можно трактовать следующим образом. Для того, чтобы определить энергию частицы (системы) с точностью  Е, необходимо проводить измерения в течение промежутка времени
Е, необходимо проводить измерения в течение промежутка времени  t >
t > 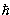 /
/  Е. Следствием этого соотношения является возможность виртуальных (ненаблюдаемых) процессов, лежащих в основе механизма взаимодействия частиц в квантовой теории поля. Две частицы взаимодействуют, обмениваясь с нарушением баланса энергии на величину
Е. Следствием этого соотношения является возможность виртуальных (ненаблюдаемых) процессов, лежащих в основе механизма взаимодействия частиц в квантовой теории поля. Две частицы взаимодействуют, обмениваясь с нарушением баланса энергии на величину  Е виртуальным (ненаблюдаемым) переносчиком взаимодействия, существующим в течение времени
Е виртуальным (ненаблюдаемым) переносчиком взаимодействия, существующим в течение времени  t <
t < 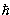 /
/  Е.
Е.
Другая трактовка соотношения  Е
Е  t
t 
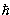 связана с понятием времени жизни нестабильного (распадающегося состояния системы или частицы). Так, если квантовая система в дискретном энергетическом состоянии живёт в среднем время
связана с понятием времени жизни нестабильного (распадающегося состояния системы или частицы). Так, если квантовая система в дискретном энергетическом состоянии живёт в среднем время 

 t, то энергетическая ширина уровня Г даётся соотношением Г
t, то энергетическая ширина уровня Г даётся соотношением Г 
 Е
Е 
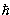 /
/  t
t 
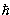 /
/  .
.
В силу крайней малости константы Планка 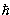 , соотношения неопределённостей не играют практически никакой роли для макроскопических тел.
, соотношения неопределённостей не играют практически никакой роли для макроскопических тел.
39. Как соотношение DЕ × Dt ³ h объясняет противоречия планетарной модели Резерфорда?
См вопрос 38