Кинематический расчет механизмов

 

3.3.1. Содержание кинематического расчета. Кинематический расчет передаточного механизма привода, связанный с типом и характером задания, частично изложен выше в объеме, необходимом для определения частоты вращения приводного двигателя. Для расчета и конструирования механизма необходимо выполнить кинематический расчет, включающий: определение частоты вращения рабочего органа n_Р, мин^-1 и каждого вала механизма n_i мин^-1, определение общего передаточного числа механизма u_M и разбивку его по ступеням передач, входящим в данный механизм.

 

3.3.2. Определение частоты вращения рабочего органа n_Р, мин^-1. Частота вращения рабочего органа машины (барабана, звездочки) во всех заданиях, кроме винтовых конвейеров (задания 19-23) и рулевых машин (задания 36-37), определяется по формуле, мин^-1

n_Р = , (3.5)

где v - линейная скорость рабочего органа (ленты, цепи, каната), м/с;

D - диаметр барабана тяговой звездочки, м.

 

Диаметр тяговой звездочки конвейера равен, мм

D = 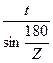, (3.6)

Где t - шаг тяговой цепи, мм;

Z - число зубьев звездочки (см. задания).

В заданиях 27, 28, 34, 35 средний диаметр швартовного барабана (турачки) определяют через диаметр швартовного каната d_K по зависимости D_ШВ.Б = 20 d_K.

В заданиях 19-23 и 36-37 частота вращения соответственно винта n_В и баллера n_б известны (см. исходные величины заданий).

 

3.3.3. Определение общего передаточного числа и разбивка его по ступеням передачи. Общее передаточное число механизма u_M определяется по формуле

u_M = 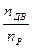= u₁ u₂ u₃, (3.7)

где n_ДВ - частота вращения ротора двигателя, мин^-1;

n_Р - частота вращения рабоего органа, определяется по формуле (3.5)

или принимается из заданий 19-23, 36, 37, мин^-1;

u₁ u₂ u₃ - передаточные числа ступеней механизма (см. табл. 3.2).

При разбивке общего передаточного числа механизма u_М по ступеням передачи учитывается требования стандартов, обеспечения нормальной смазки колес, окунанием в масляную ванну и минимальный габаритов передачи.

Учитывая эти требования, передаточное число быстроходной ступени (u_б) двухступенчатого цилиндрического редуктора (u_Р) рекомендуется определить по формуле [14].

u_б = u₁ = 1,25 √ u_Р. (3.8)

Для двухступенчатого коническо – цилиндрического редуктора число быстроходной ступени (конической передачи) принимают равным

u_б = u₁ ≤ √ u_Р. (3.9)

Значения передаточных чисел ступеней передачи и редукторов приведены в табл. 3.2, которые необходимы для определения общего передаточного числа механизма u_М.

3.3.4. Передаточное число и числа зубьев планетарных зубчатых редукторов. Согласно заданиям 11, 12, 13 и 14 кинематические схемы одно – и двухступенчатых планетарных редукторов показаны соответственно на рис. 3.2, а и рис. 3.2, б.

 

Рис. 3.2. Кинематические схемы планетарных редукторов:

 

n_ДВ = n₁ - частота вращения двигателя или ведущего вала редуктора; n_Р – частота вращения ведомого (выходного) вала редуктора или водила Н в схеме «а» и в схеме «б» водила второй ступени; 1, 1´ - солнечное зубчатое колесо соответственно первой и второй ступени; 2, 2´ - зубчатые колеса сателлиты первой и второй ступени; 3, 3´ - зубчатые колеса неподвижные первой и второй ступени; 4 - корпус редуктора

 

Передаточное число простого одноступенчатого планетарного редуктора (рис. 3.2, а) определяется по формуле [8]

, (3.10)

где z₁¸ z₃ - числа зубьев солнечного и неподвижного колеса одноступенчатого редуктора или числа зубьев солнечного и неподвижного колеса первой ступени двухступенчатого редуктора.

 

Передаточное число двухступенчатого редуктора равно

(3.11)

 

Передаточное число первой ступени ( 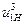)₁ рекомендуется принимать больше, чем второй ступени ( 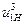)₂ с целью получения одинаковых габаритов неподвижных колес 3 и 3´. Максимальное значение передаточного числа первой ступени ( 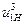)₁ принимают равным до 12,5 - 15 (см. табл. 3.2).

При проектировании планетарных передач, когда габариты колеса 3 не заданы, число зубьев z₁¸ z₂¸ z₃ определяют при соблюдении трех условий собираемости;

а) условие соосности валов центральных колес удовлетворяется следующим равенством чисел зубьев колес (без смещения производящего контура):

z₃ = z₁ + 2 z₂; (3.12)

б) для обеспечения нормального вхождения зубьев в зацепление при равных углах расположения сателлитов должно быть обеспечено условие сборки

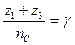, (3.13)

где n_C - число сателлитов (обычно три);

γ - целое число;

в) условие соседства - чтобы соседние сателлиты не задевали при вращении зубьями друг друга

(z₁ + z₂) sin >z₂ + 2. (3.14)

Окончательно принятые числа зубьев z₁¸ z₂¸ z₃ должны удовлетворять указанным трем условиям. Практически эти условия обеспечиваются следующим образом.

Принимают число сателлитов n_C = 3, расположенных по окружности с шаговым углом 120º, и число зубьев солнечного колеса в пределах z₁ = 15-21.

Затем из формулы (3.10) определяют число зубьев неподвижного колеса

z₃ = ( 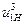- 1) z₁ - целое число зубьев.

Из условия соосности (формула 3.12) определяет число зубьев колеса сателлита.

z₂ = - целое число зубьев.

Далее проверяют условия сборки и соседства по формулам (3.13), (3.14).

По принятым окончательно числам зубьев проверяют передаточное число 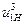.которое должно быть близким к принятому значению.

 

3.3.5. Передаточное число и числа зубьев волнового редуктора. Согласно заданиям 15, 16 и 17. 18 кинематические схемы волновых зубчатых редукторов представлены соответственно на рис. 3.3, а и рис. 3.3, б.

Передаточное число волнового редукторов (рис. 3.3, а) при закрепленном гибком колесе g от генератора h к жесткому колесу b определяется по формуле [9].

, (3.15)

где n_ДВ, n_Р - известны из предыдущего;

z_b¸z_g - числа зубьев жесткого и гибкого колес. В волновых передачах обычно принимают z_b - z_g = UK_z;

где U - число волн генератора, в двух волновых U = 2;

K_z - коэффициент разности чисел зубьев обычно K_z = 1.

Тогда z_b - z_g = 2.

 

Рис. 3.3. Кинематические схемы волновых зубчатых редукторов:

n_ДВ = n_h - частота вращения двигателя или генератора волн h; n_Р - частота вращения ведомого вала редуктора (жесткого колеса - рис. 3.3, а, гибкого колеса - рис. 3.3, б) или рабочего органа; h - генератор двухволновой роликовый (может быть дисковый, кулачковый); b - жесткое зубчатое колесо; К - корпус редуктора

 

Имея значение передаточного числа , нетрудно назначить числа зубьев z_b и z_g.

Например, при = 100, z_b = 200, z_g = 198.

Передаточное число волнового редуктора (рис. 3.3, б) при закрепленном жестком колесе b от генератора h к гибкому колесу g равно [9]

= - . (3.16)

Знак минус указывает, что вращение гибкого колеса g будет в обратную сторону вращению генератора волн h.