Метод наименьших квадратов (МНК)
Простейшую экстраполяционную модель, отражающую взаимосвязь прогнозируемого показателя с некоторой переменной, формирующей динамику этого показателя, можно записать в виде
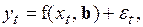
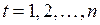 , (2.21)
, (2.21)
где 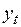 – значение
– значение 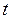 -го наблюдения прогнозируемого показателя;
-го наблюдения прогнозируемого показателя;
 – значение переменой, формирующей динамику показателя в момент времени
– значение переменой, формирующей динамику показателя в момент времени 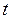 (для трендовых моделей, являющихся частным случаем экстраполяционных,
(для трендовых моделей, являющихся частным случаем экстраполяционных, 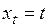 );
);
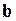 – вектор неизвестных параметров, оцениваемых по данным временного ряда;
– вектор неизвестных параметров, оцениваемых по данным временного ряда;
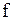 – функция, определяющая структуру трендовой модели (линейную, степенную и т.п.);
– функция, определяющая структуру трендовой модели (линейную, степенную и т.п.);
 – ненаблюдаемая случайная величина, представляющая собой ту часть вариации показателя
– ненаблюдаемая случайная величина, представляющая собой ту часть вариации показателя 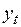 , которая не объясняется соответствующими изменениями переменной
, которая не объясняется соответствующими изменениями переменной  .
.
Чем ниже уровень вариаций около 0 возможных значений случайной величины  , тем точнее модель отражает взаимодействие переменной
, тем точнее модель отражает взаимодействие переменной 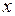 с прогнозируемым показателем
с прогнозируемым показателем  , т.е. параметры модели должны подбираться таким образом, чтобы минимизировать сумму квадратов отклонений (случайных составляющих
, т.е. параметры модели должны подбираться таким образом, чтобы минимизировать сумму квадратов отклонений (случайных составляющих  )
)
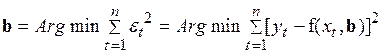 . (2.22)
. (2.22)
В общем случае поиск оптимальных параметров 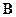 сводится к решению нелинейной экстремальной задачи. Обычно рассматривают линейный случай
сводится к решению нелинейной экстремальной задачи. Обычно рассматривают линейный случай
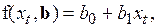 (2.23)
(2.23)
который значительно упрощает решение этой задачи.
Рассмотрим применение метода наименьших квадратов к случаю построения линейного тренда. Для этого случая (2.22) перепишется в виде
 (2.24)
(2.24)
Применяя дифференциальное исчисление для минимизации (2.24) и дифференцируя по 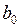 и
и  , получаем систему линейных уравнений
, получаем систему линейных уравнений
 (2.25)
(2.25)
Разделив левую и правую части этой системы на число наблюдений  и произведя замену:
и произведя замену:
 ;
;  ;
; 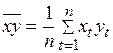 ;
;  ,
,
перепишем систему (2.25) в виде
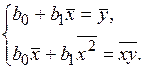 (2.26)
(2.26)