Свойства транспортной задачи.
1.ТЗ имеет оптимальное решение тогда и только тогда, когда
 (20)
(20)
2. Если план X* является оптимальным, то ему соответствует система из m+n чисел u1,…,um и v1,…,vn (называемых потенциалами), удовлетворяющих условию:
ui+vj=cij для всех xij>0, (21)
ui+vj≤cij для всех xij*=0, (22)
3. Если все числа a1,...,am и b1,...,bm - целые и выполнено условие (20), то элементы оптимального плана являются целыми числами.
4. Ранг системы векторов условий ТЗ (т.е. число линейно независимых столбцов матрицы ограничений) равен m+n-1. План перевозок X, содержащий ровно m+n-1 ненулевых перевозок, называется опорным планом (ОП) и играет роль д.б.р. в задаче ЛП. План, содержащий меньше чем m+n-1 ненулевых элементов называется вырожденным.
Пример 8. Решить следующую ТЗ методом потенциалов.
а=(40,30,20),
b=(30,25,15,20),
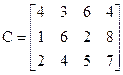
Решение. Проверим условие (20):

т.е. ТЗ имеет оптимальное решение. Строим рабочую таблицу, которая первоначально содержит только транспортные издержки, спросы и предложения.
Таблица 1.
| M1 | M2 | M3 | M4 | ||
| P1 | |||||
  P2 P2
| 1 - | 2 + | |||
 P3 P3
| 2 + z | 5 - | |||

| ai bj |
Затем в этой же таблице строим начальный ОП методом "минимальной стоимости" (об этом и других методах построения начального ОП можно прочитать, например, в [8,9]):

План является вырожденным, так как m+n-1=6, (см. свойство 4), а для X0число ненулевых перевозок равно 5.
Проверим данный план на оптимальностьприпомощи критерия (21)-(22)Сначала для xij>0 в плане X0 вычислим потенциалы по формуле(21):
u1+v2=c12=3
u1+v4=c14=4
u2+v1=c21=1 (23)
u3+v3=c33=5
u3+v4=c34=7
В этой системе 7 неизвестных и 5 уравнений, т.е. ее нельзя решить. Поэтому выбираем сами u1=0 (см. примечание ниже). Тогда из первых двух уравнений найдем: v2=3, v4=4; Из последних двух: u3=3, v3=2. Далее вычисления прерываются (следствие вырожденности плана Х0). В таких случаях вводят фиктивные перевозки, записывая в соответствующие клетки 0, но считая эти перевозки ненулевыми. Существует много способов определения фиктивного маршрута (клетки) так, чтобы система потенциалов определялась однозначно. (см., например, [8], стр. 116).
Для фиктивных перевозок мы выберем клетку (2,3) по следующим соображениям:
а) этот маршрут наиболее дешевый (c23 =2)
б) при добавлении уравнения
u2+v3=c23=2
система (23) разрешается однозначно:
u1=0, u2=0, u3=3;
v1=1, v2=3, v3=2, v4=4;
Теперь проверим выполнение неравенств (22) для нашего плана (для хij=0 в X0):
u1+v1-c11=-3<0
u1+v3-c13=-4<0
u2+v2-c22=-3<0
u2+v4-c24=-4<0
u3+v1-c31=+2>0 ←
u3+v2-c32=+2>0 ←
Видим, что критерий оптимальности не выполнен (последние два неравенства), так что план X0 неоптимален.
Надо построить новый план перевозок. Идея состоит в изменении объема перевозок по некоторым из маршрутов. Для определения этих маршрутов строим цикл - последовательность ненулевых клеток таблицы (маршрутов), в которой соседними являются две и только две ненулевые клетки одного столбика или одной строки, а последняя клетка последовательности находится либо в том же столбике, либо в той же строке, что и начальная клетка последовательности. "Вершины" цикла (т.е. клетки, вошедшие в цикл) и показывают те маршруты, по которым нужно изменить объемы перевозок. Остается определить начальную клетку цикла - клетку с наихудшей (положительной) оценкой в системе (24).
В данном случае можно взять как клетку (3,1) так и (3,2). Возьмем клетку (3,1) и напишем в эту клетку пока неизвестное число z (в таблицу 1). Начиная с этой клетки, строим цикл (см. таблицу 1): (3,1) → (3,3) → (2,3) → (2,1). Впишем в начальную клетку знак "+" и далее последовательно ''-'', "+" по вершинам цикла, как это показано в таблице 1. Значение z (объем новых перевозок по маршруту (3,1)) определяется из условия: z=min{  }, где
}, где  - объем перевозок по маршрутам, отмеченным знаком "-". Итак z=min{15,30}=15. Эту величину 15 отнимаем из объема перевозок, отмеченных знаком “-“, и прибавляем к объемам перевозок, отмеченных знаком "+" (балансируем). Результаты записываем в новую таблицу, перенося туда остальные перевозки без изменения:
- объем перевозок по маршрутам, отмеченным знаком "-". Итак z=min{15,30}=15. Эту величину 15 отнимаем из объема перевозок, отмеченных знаком “-“, и прибавляем к объемам перевозок, отмеченных знаком "+" (балансируем). Результаты записываем в новую таблицу, перенося туда остальные перевозки без изменения:
Таблица 2.
| M1 | M2 | M3 | M4 | ||
  P1 P1
| 4 + | ||||
| P2 | |||||
 P3 P3
| 4 + z | 7 - | - | ||

| ai bj |
Получим новый ОП:
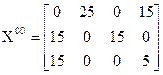
Видно, что он невырожденный, следовательно при проверке на оптимальность плана X00 система (21) разрешится однозначно (не нужно будет вводить фиктивные перевозки).
Самостоятельно проверьте, что ОП X00 неоптимален, и что на третьей итерации получается оптимальный опорный план (выполнены все неравенства (22)):
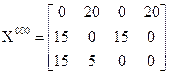
Вычислите суммарные стоимости перевозок по X0, X00, X000 по формуле (5) и убедитесь в оптимальности плана перевозок X000.
Как видно из решенного примера, алгоритм метода потенциалов следующий:
1) Занести данные задачи (транспортные издержки, спросы и предложения) в специальную рабочую таблицу;
2) Вычислить начальный ОП;
3) Проверить ОП на оптимальность;
3.1) Найти значения потенциалов для данного ОП по формуле (21); если ОП вырожденный, то ввести фиктивные перевозки;
3.2) Проверить выполнение неравенств (22): если они все выполнены, то данный ОП оптимален - вычисления прекратить; если нет, то перейти к пункту 4;
4) Построить новый ОП;
4.1) Построить цикл;
4.2) Изменить по вершинам цикла объемы перевозок;
4.3) Заполнить новую рабочую таблицу и перейти к пункту 3.
Примечанияк методу потенциалов.
1. Систему потенциалов однозначно можно вычислить только для невырожденного ОП, при этом одному из потенциалов нужно придать произвольное значение (обычно u1=0, т.к. всистеме ограничений закрытой ТЗ имеется одно линейно зависимое ограничение).
2. В случае вырожденного ОП нужно ввести фиктивные перевозки с таким расчетом, чтобы из системы (21) однозначно вычислить все потенциалы.
3. Цикл всегда существует и единственен для каждой свободной клетки таблицы (для невырожденного ОП).
4. Если для какой-то свободной клетки (xij= 0) оптимального ОП в соотношении (22) достигается строгое равенство, то это говорит о неединственности оптимального ОП.
В зависимости от содержательной трактовки чисел сij транспортная задача может быть поставлена на минимизацию суммарного расстояния или времени Пробега транспорта или на минимизацию расхода горючего, более общей является открытая модель ТЗ (когда не требуется выполнения равенства (20)) и сетевая постановка ТЗ (когда один и тот же пункт выступает в роди производителя и потребителя),. Открытые ТЗ решаются путем сведения к замкнутой ТЗ (вводятся фиктивные потребители или производители), а для решения сетевых ТЗ существуют специальные методы (например, метод динамического программирования).
§6. Решение оптимизационных задач с помощью
модуля MS Excel "Поиск решения".
Программа MS Excel позволяет решать оптимизационные задачи с помощью модуля "Поиск решения".
Постановка задачи.Предприятие, располагающее ресурсами сырья трёх видов 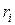 ,
, 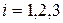 , может производить продукцию четырёх видов
, может производить продукцию четырёх видов 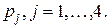 В таблице указаны затраты ресурсов
В таблице указаны затраты ресурсов 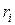 на изготовление 1 ед. продукции
на изготовление 1 ед. продукции 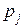 , объёмы ресурсов, ограничения на объемы продаж и прибыль, получаемая от продажи 1 ед. продукции
, объёмы ресурсов, ограничения на объемы продаж и прибыль, получаемая от продажи 1 ед. продукции 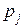 . Определить ассортимент выпускаемой продукции, при котором полученная прибыль будет максимальной.
. Определить ассортимент выпускаемой продукции, при котором полученная прибыль будет максимальной.
В предлагаемой задаче:
Предприятие – это институт;
Ресурсы сырья – услуги в часах: Преподаватели, Компьютерный класс, Практика;
Производство - обучение студентов;
Продукция – следующие профессии: Руководитель, Секретарь, Программист;
Прибыль - Рейтинг института от трудоустройства одного специалиста.
Так как под производством подразумевается обучение студентов, то необходимо обучить всех студентов. В группе N=22 студента.
Метод решения. Комментарии. Для решения задачи о планировании производства введем переменные 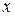 i, i=1,...,n, где
i, i=1,...,n, где 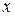 i будет означать объем выпуска i-го вида продукции. Очевидно,
i будет означать объем выпуска i-го вида продукции. Очевидно,  , i=1,...,n и
, i=1,...,n и  . Составим систему ограничений. Имеем:
. Составим систему ограничений. Имеем:
 - единиц ресурса
- единиц ресурса 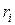 тратится на выпуск продукции
тратится на выпуск продукции 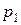 ;
;
. . . . . . . . . .
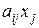 - единиц ресурса
- единиц ресурса 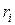 тратится на выпуск продукции
тратится на выпуск продукции 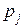 ;
;
. . . . . . . . . .
 - единиц ресурса
- единиц ресурса 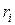 тратится на выпуск продукции
тратится на выпуск продукции 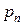 .
.
Всего же имеется ресурса 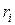 в количестве
в количестве  . Таким образом, имеет место неравенство
. Таким образом, имеет место неравенство
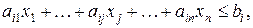 (24)
(24)
Составим целевую функцию. Очевидно, прибыль от реализации продукта 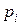 в количестве
в количестве 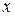 I единиц будет равна
I единиц будет равна 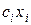 рублей, а общая прибыль от продажи всех видов продукции
рублей, а общая прибыль от продажи всех видов продукции  составит
составит
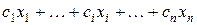 (25)
(25)
рублей.
Таким образом, мы получили задачу линейного программирования:
 (26)
(26)
 (27)
(27)
Указания(Пример на закладке "Оптимизация1" книги "оптимизация.xls".
Задачу можно решить с использованием "Решателя" MS Exel-таблиц следующим образом. Задать в ячейках D12-G12 начальные значения неизвестных (обычно полагают их равными нулю). Ввести в ячейки J3-J5 три формулы — правые части неравенств системы ограничений. Например, первому неравенству системы 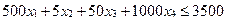 будет соответствовать формула
будет соответствовать формула
=СУММПРОИЗВ(D$12:G$12;D3:G3), занесённая в ячейку J3. В ячейку D9 внесите сумму обученных студентов. Далее в одну из свободных ячеек, например, в ячейку D14 введите формулу целевой функции.
Затем в меню "Сервис" необходимо выбрать команду "Поиск решения", которая активизирует одноимённое окно (если такой команды в меню нет, следует сперва открыть диалог меню "Сервис" ¾ "Надстройки" и отметить пункт "Поиск решения").
В этом окне прежде всего необходимо установить целевую ячейку — в нашем случае это D14. Если задача линейного программирования состоит в максимизации целевой функции, то тогда необходимо это указать, установив флажок. Изменяемые ячейки — это ячейки, соответствующие переменным задачи, т.е. в нашем случае это ячейки D12-G12.
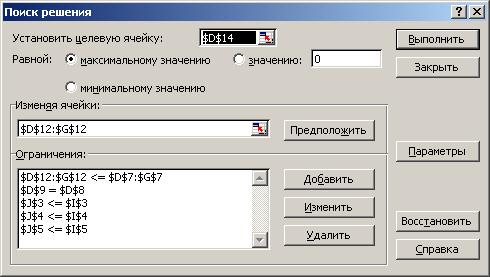
Для ввода неравенств-ограничений задачи нажмите кнопку "Добавить". В появившемся диалоговом окне в левом поле укажите ячейку, в которой находится левая часть неравенства (в нашем случае это J3), затем в правое поле введите ячейку, которая соответствует правой части неравенства (ячейка I3); и, наконец, выберите нужный знак неравенства. Теперь нажмите кнопку "OK". Первое неравенство введено. Аналогично вводятся другие неравенства.
В случае, если одно из неравенств набрано неверно, то ошибку можно исправить. Для этого необходимо выделить это неравенство и нажать кнопку "Изменить". Удалить неравенство можно, нажав соответствующую кнопку.
Нажмите кнопку "Опции". В одноимённом диалоговом окне можно установить число итераций (по умолчанию равно 100), точность вычислений (по умолчанию 0,000001), допустимое отклонение (по умолчанию 5%), максимальное время работы (по умолчанию 100 секунд). В этом же окне устанавливается типы модели — в нашем случае модель линейная и переменные неотрицательны. Установите соответствующие флажки. Нажмите кнопку "OK", а затем – кнопку "Решать".