Коэффициент корреляции Пирсона
Термин «корреляция» был введен в науку выдающимся английским естествоиспытателем Френсисом Гальтоном в 1886 г. Однако точную формулу для подсчета коэффициента корреляции разработал его ученик Карл Пирсон.
Коэффициент характеризует наличие только линейной связи между признаками, обозначаемыми, как правило, символами X и Y. Формула расчета коэффициента корреляции построена таким образом, что, если связь между признаками имеет линейный характер, коэффициент Пирсона точно устанавливает тесноту этой связи. Поэтому он называется также коэффициентом линейной корреляции Пирсона. Если же связь между переменными X и Y не линейна, то Пирсон предложил для оценки тесноты этой связи так называемое корреляционное отношение.
Величина коэффициента линейной корреляции Пирсона не может превышать +1 и быть меньше чем -1. Эти два числа +1 и -1 — являются границами для коэффициента корреляции. Когда при расчете получается величина большая +1 или меньшая -1 — следовательно произошла ошибка в вычислениях.
Знак коэффициента корреляции очень важен для интерпретации полученной связи. Подчеркнем еще раз, что если знак коэффициента линейной корреляции — плюс, то связь между коррелирующими признаками такова, что большей величине одного признака (переменной) соответствует большая величина другого признака (другой переменной). Иными словами, если один показатель (переменная) увеличивается, то соответственно увеличивается и другой показатель (переменная). Такая зависимость носит название прямо пропорциональной зависимости.
Если же получен знак минус, то большей величине одного признака соответствует меньшая величина другого. Иначе говоря, при наличии знака минус, увеличению одной переменной (признака, значения) соответствует уменьшение другой переменной. Такая зависимость носит название обратно пропорциональной зависимости.
В общем виде формула для подсчета коэффициента корреляции такова:
 (7)
(7)
где хi — значения, принимаемые в выборке X,
yi — значения, принимаемые в выборке Y;
 — средняя по X,
— средняя по X, 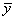 — средняя по Y.
— средняя по Y.
Расчет коэффициента корреляции Пирсона предполагает, что переменные Х и У распределены нормально.
В формуле (7) встречается величина  при делении на n (число значений переменной X или Y) она называется ковариацией. Формула (7) предполагает также, что при расчете коэффициентов корреляции число значений переменной Х равно числу значений переменной Y.
при делении на n (число значений переменной X или Y) она называется ковариацией. Формула (7) предполагает также, что при расчете коэффициентов корреляции число значений переменной Х равно числу значений переменной Y.
Число степеней свободы k=n-2.
Пример 3.10 школьникам были даны тесты на наглядно-образное и вербальное мышление. Измерялось среднее время решения заданий теста в секундах. Исследователя интересует вопрос: существует ли взаимосвязь между временем решения этих задач? Переменная X — обозначает среднее время решения наглядно-образных, а переменная Y— среднее время решения вербальных заданий тестов [2].
Решение. Представим исходные данные в виде таблицы 4, в которой введены дополнительные столбцы, необходимые для расчета по формуле (7).
Таблица 4
| № испытуемых | x | y | хi- 
| (хi-  )2 )2
| yi- 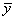
| (yi- 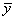 )2 )2
| 
|
| -16,7 | 278,89 | -7,2 | 51,84 | 120,24 | |||
| -3,7 | 13,69 | -17,2 | 295,84 | 63,64 | |||
| -2,7 | 7,29 | -7,2 | 51,84 | 19,44 | |||
| 8,3 | 68,89 | 3,8 | 14,44 | 31,54 | |||
| -7,7 | 59,29 | 2,8 | 7,84 | -21,56 | |||
| -0,7 | 0,49 | 6,8 | 46,24 | -4,76 | |||
| 3,3 | 10,89 | -4,2 | 17,64 | -13,86 | |||
| 3,3 | 10,89 | -7,2 | 51,84 | -23,76 | |||
| 8,3 | 68,89 | 10,8 | 116,64 | 89,64 | |||
| 8,3 | 68,89 | 18,8 | 353,44 | 156,04 | |||
| Сумма | 588,1 | 1007,6 | 416,6 | ||||
| Среднее | 35,7 | 24,2 |
Рассчитываем эмпирическую величину коэффициента корреляции по формуле (7):

Определяем критические значения для полученного коэффициента корреляции по таблице Приложения 3. При нахождении критических значений для вычисленного коэффициента линейной корреляции Пирсона число степеней свободы рассчитывается как k = n – 2 = 8.
ккрит=0,72 > 0,54 , следовательно, гипотеза Н1 отвергается и принимается гипотеза H0, иными словами, связь между временем решения наглядно-образных и вербальных заданий теста не доказана.