Транспортная задача линейного программирования

Цель работы: закрепление на практике методики составления экономико-математических моделей транспортного типа и решения задач линейного программирования, относящихся к типу транспортных задач.

Исходные положения. К задачам линейного программирования транспортного типа относятся задачи о перевозках некоторого однородного продукта (груза, товара) из пунктов отправления (от поставщиков) в пункты назначения (к потребителям) при обеспечении минимальных затрат на перевозки или минимального времени доставки. Транспортная задача линейного программирования нашла практическое применение на транспорте и в промышленности.

Постановка задачи: некоторый однородный продукт, сосредоточенный у m поставщиков А_i в количестве а_i (i=1,2,...m) единиц соответственно, необходимо доставить n потребителям В_j в количестве b_j (j=1,2,...n) единиц. Известна стоимость С_ij перевозки единицы груза от i-го поставщика к j-му потребителю. Необходимо составить план перевозок, позволяющий вывезти все грузы, полностью удовлетворить потребности при минимальных затратах.

Обозначим через Х_ij - количество единиц груза, которое необходимо перевезти от i-го поставщика к j-му потребителю. Условие задачи можно записать в виде таблицы:

Поставщики	Потребители	Предложение
В₁	В₂	…	В_n
А₁	С₁₁ Х₁₁	С₁₂ Х₁₂	…	С_1n Х_1n	а₁
А₂	С₂₁ Х₂₁	С₂₂ Х₂₂	…	С_2n Х_2n	а₂
…	…	…	…	…	…
А_m	С_m1 Х_m1	С_m2 Х_m2	…	С_mn Х_mn	А_m
Спрос	b₁	b₂	…	b_n	åa_i = åb_j

Тогда математическая модель задачи сведется к нахождению минимума функции цели, выражающей суммарные затраты на перевозки всего груза:

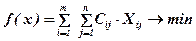
при следующих ограничениях:

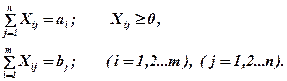
Если выполняется условие , т.е. спрос равен предложению, то задача соответствует открытой модели. Если же предложение превышает спрос, вводится фиктивный потребитель с потребностью, равной разнице между предложением и спросом, в противном случае, когда спрос больше, чем предложение - вводится фиктивный поставщик с запасом, также равным разнице этих сравниваемых величин.

Тогда ограничения математической модели примут вид:

1-й случай

Вводится фиктивный потребитель В_n₊₁ , потребность которого в продукции равна

2-й случай

Вводится фиктивный поставщик А_m₊₁, предложение которого равно

Стоимость перевозки груза от фиктивного поставщика или к фиктивному потребителю принимается равной 0 т.к. груз в обоих случаях реально не перевозится. После преобразования задача принимает вид закрытой модели и, как и все задачи транспортного типа может быть решена как с помощью симплекс-метода, так и с помощью распределительного метода или же методом потенциалов.

Примеры решения задач. Закрытая модель.

Поставщики	Потребители	Предложение
В₁	В₂	В₃	В₄	В₅
А₁	Х₁₁	Х₁₂	Х₁₃	Х₁₄	Х₁₅
А₂	Х₂₁	Х₂₂	Х₂₃	Х₂₄	Х₂₅
А₃	Х₃₁	Х₃₂	Х₃₃	Х₃₄	Х₃₅
А₄	Х₄₁	Х₄₂	Х₄₃	Х₄₄	Х₄₅
Спрос

Составить план перевозок, позволяющий вывезти все грузы, полностью удовлетворить потребности и имеющий min стоимость.

(10Х₁₁ + 7Х₁₂ + 4Х₁₃ + Х₁₄ + 4Х₁₅ + 2Х₂₁ + 7Х₂₂ + 10Х₂₃ + 6Х₂₄ + 11Х₂₅ + 8Х₃₁ + 5Х₃₂ + 3Х₃₃ + 2Х₃₄ + 2Х₃₅ + 11Х₄₁+ 8Х₄₂ + 12Х₄₃ + 16Х₄₄ + 13Х₄₅) ® min.

Система ограничений имеет вид:

Х₁₁ + Х₁₂ + Х₁₃ + Х₁₄ + Х₁₅ = 100

Х₂₁ + Х₂₂ + Х₂₃ + Х₂₄ + Х₂₅ = 250

Х₃₁ + Х₃₂ + Х₄₄ + Х₃₄ + Х₃₅ = 200

Х₄₁ + Х₄₂ + Х₄₃ + Х₄₄ + Х₄₅ = 300

Х₁₁ + Х₂₁ + Х₃₁ + Х₄₁ = 200

Х₁₂ + Х₂₂ + Х₃₂ + Х₄₂ = 200

Х₁₃ + Х₂₃ + Х₃₃ + Х₄₃ = 100

Х₁₄ + Х₂₄ + Х₃₄ + Х₄₄ = 100

Х₁₅ + Х₂₅ + Х₃₅ + Х₄₅ = 250

Решение задачи на ЭВМ дает следующий результат:

f(X) = 4150 X₅ = 50 X₉ = 50 X₁₇ = 200

X₄ = 50 X₆ = 200 X₁₅ = 200 X₁₈ = 100.

Открытая модель.

Составим план перевозок грузов от 4-х поставщиков А_i (i=1,2,3,4) соответственно в количествах 100, 400, 100 и 100 единиц к пяти потребителям В_j (j=1,2,3,4,5) соответственно в количествах 50, 100, 150, 200, 250 единиц с наименьшей стоимостью перевозок. Стоимость перевозок единицы груза представлена матрицей С:

Решение.

Суммарные запасы .

Суммарные потребности

Суммарный спрос превышает суммарное предложение, следовательно, модель открытая (2-й случай). Необходимо ввести фиктивного поставщика А₅ с запасами 750-700=50 единиц продукта.

Поставщики	Потребители	Предложение
В₁	В₂	В₃	В₄	В₅
А₁	Х₁₁	Х₁₂	Х₁₃	Х₁₄	Х₁₅
А₂	Х₂₁	Х₂₂	Х₂₃	Х₂₄	Х₂₅
А₃	Х₃₁	Х₃₂	Х₃₃	Х₃₄	Х₃₅
А₄	Х₄₁	Х₄₂	Х₄₃	Х₄₄	Х₄₅
(А₅)	Х₅₁	Х₅₂	Х₅₃	Х₅₄	Х₅₅	(50)
Спрос

Тогда математическая модель задачи примет вид:

(Х₁₁ + 6Х₁₂ + 8Х₁₃ + 12Х₁₄ + 16Х₁₅ + 16Х₂₁ + 10Х₂₂ + 8Х₂₃ +

+ 6Х₂₄ + 15Х₂₅ + 4Х₃₁ + Х₃₂ + 9Х₃₃ + 11Х₃₄ + 13Х₃₅ + 3Х₄₁ +

+ 2Х₄₃ + 7Х₄₃ + 7Х₄₄ + 15Х₄₅ + 0Х₅₁ + 0Х₅₂ + 0Х₅₃ + 0Х₅₄ +

+ 0Х₅₅) ® min.

Система ограничений имеет вид:

Х₁₁ + Х₁₂ + Х₁₃ + Х₁₄ + Х₁₅ = 100

Х₂₁ + Х₂₂ + Х₂₃ + Х₂₄ + Х₂₅ = 400

Х₃₁ + Х₃₂ + Х₃₃ + Х₃₄ + Х₃₅ = 100

Х₄₁ + Х₄₂ + Х₄₃ + Х₄₄ + Х₄₅ = 100

Х₅₁ + Х₅₂ + Х₅₃ + Х₅₄ + Х₅₅ = 50

Х₁₁ + Х₂₁ + Х₃₁ + Х₄₁ + Х₅₁ = 50

Х₁₂ + Х₂₂ + Х₃₂ + Х₄₂ + Х₅₂ = 100

Х₁₃ + Х₂₃ + Х₃₃ + Х₄₃ + Х₅₃ = 150

Х₁₄ + Х₂₄ + Х₃₄ + Х₄₄ + Х₅₄ = 200

Х₁₅ + Х₂₅ + Х₃₅ + Х₅₅ + Х₅₅ = 250

Решение задачи на ЭВМ дает следующий результат:

f(X) = 5450 X₈ = 100 X₁₅ = 100

X₁ = 50 X₉ = 200 X₁₇ = 100

X₃ = 50 X₁₀= 100 X₂₅ = 50.

Порядок выполнения работы.

1. Изучение студентами исходных положений и экономико-математической постановки транспортной задачи линейного программирования.

2. Разбиение студенческой подгруппы на бригады и получение ими исходного задания.

3. Построение математической модели в общем виде, приведение модели к каноническому виду и составление матрицы исходных данных для расчета задачи на ЭВМ.

4. При "ручном" способе расчета на калькуляторах, задача решается распределительным методом или методом потенциалов.

4. Расчет на ЭВМ производится с помощью программ "Решение задач линейного программирования симплекс-методом" или "Транспортная задача линейного программирования", реализованных на ПЭВМ в табличном процессоре “Excel” или комплексе программ для учебного процесса "Prima".

5. Анализ и экономическая интерпретация результатов моделирования на ЭВМ, которые должны быть отражены в выводах по работе.

Отчет по работе должен содержать

1. Цель и экономико-математическую постановку транспортной задачи линейного программирования.

2. Экономико-математическую модель в общем и каноническом виде, исходные данные для расчета на ЭВМ.

3. Результаты моделирования на ЭВМ и их экономическую интерпретацию.

4. Выводы по лабораторной работе должны содержать анализ и экономическую интерпретацию результатов моделирования.