Расчет и оптимизация сетевого графика
Цель работы: знакомство студентов с методикой построения сетевого графика и его линейной диаграммы (графика Ганта), расчет основных временных параметров сетевого графика и его оптимизация на ЭВМ. Закрепление теоретического лекционного материала и материала, изучаемого самостоятельно.
Исходные положения. Сетевые модели используются при планировании и управлении ходом разработок новых видов продукции и процессов их производства. Сетевые модели позволяют изображать календарный план графически, показывают последовательность и время начала и окончания каждой из работ. Это важно для оперативного контроля за ходом выполнения работ и своевременного принятия регулирующих решений при возникновении отклонений от плана.
Основные понятия. Главными элементами сетевой модели являются событие и работа. Работа – любой процесс (действие), приводящий к определенному результату – событию. Если событие является результатом нескольких произведенных работ, то момент свершения такого события наступает с окончанием самой длительной работы, входящей в данное событие. Кроме работ действительных, требующих затрат времени и ресурсов, существуют ожидания (время естественных технологических процессов, например, остывание, высыхание, затвердевание и т.д.) и фиктивные работы(зависимости), временем выполнения и затратами ресурсов которых можно пренебречь (например, сигнал о результатах выполнения предыдущих работ, телефонное сообщение).
Работы на графиках изображаются стрелками (фиктивные работы – пунктирными стрелками). Длительность работы проставляется над стрелкой. События изображаются кругом, разделенным на четыре сектора (рис. 1.1).
 |
Рис. 1.1. Изображение события на сетевом графике
Обозначения: i – номер события;
tp(i) – ранний срок наступления i – го события;
tn(i)– поздний срок наступления i – го события;
R(i) – резерв времени i – го события.
Для каждой работы имеется предшествующее (i) и последующее (j) события.
Непрерывная технологическая цепочка работ составляет путь, а каждый путь, соединяющий исходное и завершающее события, называется полным. Полный путь, обладающий наибольшей суммарной продолжительностью работ, называется критическим. Это наиболее напряженный путь, не обладающий резервами времени и определяющий сроки завершения всего комплекса работ.
Все остальные полные пути менее длительные и менее напряженные. Работы, лежащие на таких путях имеют резервы времени.
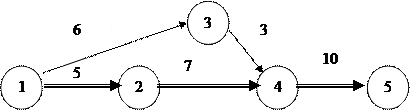
исходное предшествующее последующее завершающее
событие событие для работы 2-7 событие событие
Рис. 1.2. Сетевой график
Полные пути: 1-3-4-5 и 1-2-4-5 (критический).
Поскольку сетевой график вычерчивается без масштаба времени, он недостаточно нагляден для определения тех работ, которые должны выполняться в каждый момент времени. Поэтому в случае небольшого проекта его следует дополнить линейной диаграммой (графиком Ганта).
При построении линейной диаграммы каждая работа изображается параллельным оси времени отрезком, длина которого равна продолжительности этой работы. Фиктивная работа нулевой продолжительности изображается точкой. События i и j , начало и конец работы (i-j) помещают соответственно в начале и конце отрезка. Отрезки располагают один под другим, сверху вниз в порядке возрастания индекса i, а при одном и том же i – в порядке возрастания индекса j. Абсцисса самого правого конца последнего отрезка определит критическое время выполнения всего комплекса работ (рис. 1.3).
При календарном планировании менеджеру необходимо знать, какое количество исполнителей должно быть задействовано при выполнении комплекса работ в соответствующие промежутки времени. Для этого строится эпюра загрузки работников (рис. 1.4). При построении эпюры загрузки работников для каждого момента начала или окончания очередной работы подсчитывается общее количество исполнителей и строится столбиковая диаграмма. Система координат при построении диаграммы имеет в качестве абсциссы ось времени, а в качестве ординаты – количество работников. Высота столбца соответствуют суммарному количеству исполнителей, задействованных на всех работах, выполняемых в данный момент времени. Ширина столбца соответствует промежутку времени, в течение которого количество исполнителей работ не изменяет своего значения. Возможно построение нескольких эпюр загрузки, отдельно по каждой категории работников.
Допустим работу 1-2 выполняют 2 человека, работу 1-3 выполняют 3 человека, работу 2-4 выполняют 4 человека, работу 3-4 выполняют 2 человека, работу 4-5 выполняют 3 человека.
 |
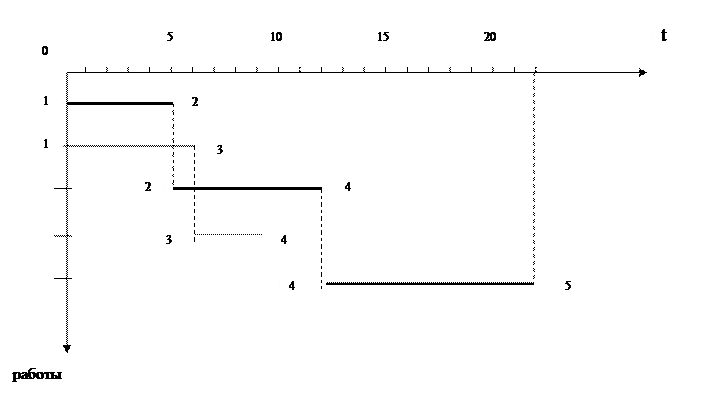Рис. 1.3. График Ганта (линейная диаграмма сетевого графика)
 |
Рис. 1.4. Эпюра загрузки исполнителей работ
Среди резервов времени работ выделяют четыре разновидности резервов (рис. 1.5).
Под полным Rп(i,j) резервом времени работы (i-j) понимается допустимый сдвиг срока ее выполнения, не меняющий срока свершения завершающего события всего комплекса работ.
Под свободным Rс(i,j) резервом времени работы (i-j) понимается допустимый сдвиг срока ее выполнения, не меняющий раннего срока ее последующего события tp(j).
Под частным Rч(i,j) резервом времени работы (i-j) понимается допустимый сдвиг срока ее выполнения, не меняющий позднего срока предшетвующего ей события tn(i).
Под независимым Rн(i,j) резервом времени работы (i-j) понимается допустимый сдвиг срока ее выполнения, не меняющий и раннего срока ее последующего события tp(j), и позднего срока предшествующего ей события tn(i)
Примечание. Резервы времени работы (i-j) могут состоять из двух временных отрезков, если интервал продолжительности работы t(i,j) занимает промежуточное место между двумя его крайними положениями, изображенными на графиках.
Свободный, частный и независимый резервы являются частями полного. Аналитически все резервы вычисляются по следующим формулам:
Полный резерв
Rn(i,j) = tn(j) - tp(i) - t(i,j) (1.1)
Частный резерв
Rr(i,j) = tn(j) – tn(i) - t(i,j) (1.2)
или
Rч(i,j) = Rn(i,j) – R(i) (1.3)
Свободный резерв
Rч(i,j) = tр(j) – tр(i) - t(i,j) (1.4)
или
Rс(i,j) = Rn(i,j) – R(j) (1.5)
Независимый резерв
Rн(i,j) = tр(j) – tn(i) - t(i,j) (1.6)
или
Rн(i,j) = Rn(i,j) – R(j) – R(i) (1.7)
 |
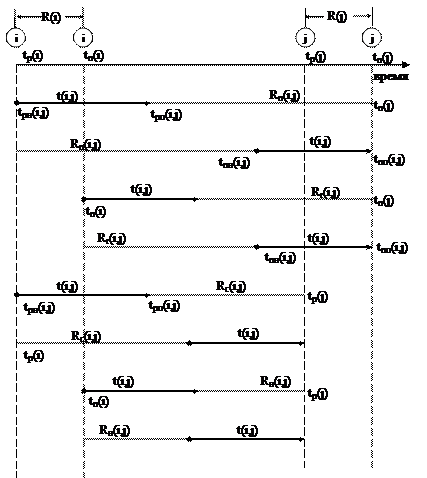Рис. 1.5. Графическое изображение резервов времени
событий и работ на шкале времени
Из приведенных формул следует, что полный резерв данной работы может быть использован на всех работах подкритических путей, через нее проходящих. Свободный резерв можно использовать на данной работе и всех работах, последующих за ней. Независимый резерв можно использовать только на данной работе.
Оптимизация сетевого графика производится путем перераспределения взаимозаменяемых сотрудников с менее загруженных работ, имеющих большие резервы времени, на работы, производящиеся в то же самое время и лежащие на критическом пути. В результате сокращается длительность критического пути и возрастает напряженность работы на остальных. При оптимизации используется следующая система уравнений.
где Тр и Тk – трудоемкости, соответственно, работы, имеющей резерв и работы, лежащей на критическом пути;
tр и tk - длительности данных работ;
Wр и Wk - число исполнителей на этих работах;
х - количество переводимых людей;
y - время сокращения критического пути.
Пример выполнения лабораторного задания.
Допустим, при планировании выполнения некоторого комплекса работ, определена их трудоемкость и число исполнителей (табл. 1.1).
Таблица 1.1 – Исходные данные
| Код работы (i,j) | Трудоемкость работы Т(i,j), нормо-ч | Число исполнителей работы W(i,j), чел |
| 1-2 | ||
| 1-3 | ||
| 2-3 | ||
| 2-4 | ||
| 2-5 | ||
| 3-4 | ||
| 3-6 | ||
| 4-5 | ||
| 4-6 | ||
| 4-7 | ||
| 5-7 | ||
| 6-7 |
Требуется:
1. По данным табл. 1 рассчитать с помощью микрокалькулятора или электронной таблицы:
а) Продолжительность каждой работы в днях.
б) Временные параметры каждого события.
2. Построить сетевой график, учитывая правила его построения, указать внутри событий номер, ранний и поздний сроки свершения и резерв времени, выделить критический путь.
3. Построить линейную диаграмму сетевого графика, выделив критический путь, и эпюру загрузки работников.
4. Рассчитать на ЭВМ:
а) Полный и свободный резервы каждой из работ.
б) Критический путь (какие события он включает) и полное время выполнения всего комплекса работ.
в) Провести оптимизацию сетевого графика.
5. Рассчитать частный и независимый резервы времени каждой работы, а также ранние и поздние сроки начала и окончания работ.
6. Составить таблицы временных параметров работ и событий.
Оформление результатов расчетов.
1. Рассчитываем на микрокалькуляторе продолжительность каждой работы t(i,j) в днях по формуле:
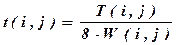
и записываем результаты в таблицу 1.2.
Таблица 1.2 – Расчет длительности выполнения работ
| Код работы | Т(i,j) | W(i,j) | t(i,j) |
| 1-2 | |||
| 1-3 | |||
| 2-3 | |||
| 2-4 | |||
| 2-5 | |||
| 3-4 | |||
| 3-6 | |||
| 4-5 | |||
| 4-6 | |||
| 4-7 | |||
| 5-7 | |||
| 6-7 |
2. Строим сетевой график
Рассчитываем временные параметры событий и наносим их на график в каждый кружок, как показано на рис. 1.1. Рассчитываем ранние сроки свершения каждого события:
1) если событию j предшествует одно событие i, т.е.
 |
,
то tp(j) рассчитываем по формуле:
tp(j) = tp(i) + t(i,j)
2) если событию j предшествует несколько событий i, т.е.
 |
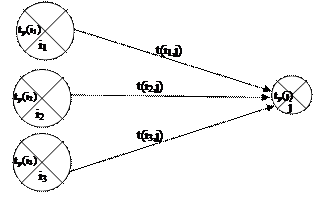то tp(j) рассчитываем по формуле:
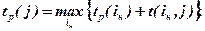
Расчет ранних сроков свершения событий ведется от первого события к последнему, т.е. слева направо. При этом tp1 = 0. Рассчитываем поздние сроки свершения каждого события.
Расчет ведется от последнего события к первому, т.е. справа налево. При этом для последнего события tp = tn.
1) если у события i одно последующее событие, т.е.
 |
,
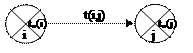то tn(i) рассчитывается по формуле:
tn(i) = tn(j) - t(i,j)
2) если у события i несколько последующих событий, т.е.
 |
то расчет tn(i) ведется по формуле:
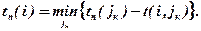
Резервы времени событий рассчитываем по формуле:
R(i) = tn(i) – tp(i).
Полученные результаты расчета заносим в соответствующие сектора на сетевом графике, после чего он примет вид:
3. Строим график Ганта (линейную диаграмму)
4. Строим эпюру загрузки работников
 |
4. Проводим расчет полного и свободного резервов времени работ на ЭВМ.
Указания по проведению расчетов на ЭВМ
В МЕНЮ лабораторных работ PRIMA выберите с помощью клавиши <¯> работу по расчету сетевого графика. Нажмите клавишу <Enter> и приступайте к работе.
Протокол диалогового режима расчетов
ПРОГРАММА РАСЧЕТА И ОПТИМИЗАЦИИ СЕТЕВОГО ГРАФИКА
РАБОТЫ НА СЕТЕВОМ ГРАФИКЕ (ДЕЙСТВИТЕЛЬНЫЕ, ОЖИДАНИЯ И ФИКТИВНЫЕ) ОБОЗНАЧАЮТСЯ СТРЕЛКАМИ , СОБЫТИЯ ОБОЗНАЧАЮТСЯ КРУЖКАМИ
Введите:
Число событий в сети: 7 <Enter>
Число работ в сети: 12 <Enter>
…………………………….. Ввести код работы номер 1
Номер события, из которого выходит работа ….1 <Enter>
Номер события, в которое входит работа …..… 2 <Enter>
Продолжительность выполнения работы ….…. 2 <Enter>
……………………………………………………..
………………………………. Ввести код работы номер 2
Номер события, из которого выходит работа ….1 <Enter>
Номер события, в которое входит работа …..… 3 <Enter>
Продолжительность выполнения работы ….…. 5 <Enter>
……………………………………………………..
………………………………. Ввести код работы номер 3
Номер события, из которого выходит работа ….2 <Enter>
Номер события, в которое входит работа …...… 3 <Enter>
Продолжительность выполнения работы …..…. 2 <Enter>
……………………………и т.д.………………………..
………………………………. Ввести код работы номер 12
Номер события, из которого выходит работа ….6 <Enter>
Номер события, в которое входит работа …..… 7 <Enter>
Продолжительность выполнения работы …….. 2 <Enter>
……………………………………………………..
Были ли при вводе ошибки …………….. (1 - да) <Enter>
Расчет резервов времени работ
| Код работы | Длительность работы | Полный резерв | Свободный резерв | Поздний срок начала работы | Коэффициент загруженности |
| 1-2 | 0,67 | ||||
| 1-3 | 1,00 | ||||
| 2-3 | 0,67 | ||||
| 2-4 | 0,67 | ||||
| 2-5 | 0,42 | ||||
| 3-4 | 1,00 | ||||
| 3-6 | 0,56 | ||||
| 4-5 | 0,67 | ||||
| 4-6 | 0,67 | ||||
| 4-7 | 1,00 | ||||
| 5-7 | 0,50 | ||||
| 6-7 | 0,50 |
Продолжить … ? <Enter>
Расчет сроков свершения событий и их резервов
| Событие | Поздний срок наступления события | Ранний срок наступления события | Полный резерв времени события |
Критический путь = 16 дней
1 3 4 7
Если необходимо исправить ошибки (1 - да) <Enter>
Будете оптимизировать: … (1 - да) 1 <Enter>
Для работ (1-3) и 1-2
Введите количество исполнителей
для работы (1-3) 4 <Enter>
для работы 1-2 5 <Enter>
Для работ (1-3) и 1-2
Количество переводимых людей ….…………0,65
Время сокращения работы ………………….. 0,70
Для работ (3-4) и 3-6
Введите количество исполнителей
для работы (3-4) 3 <Enter>
для работы 3-6 4 <Enter>
Для работ (3-4) и 3-6
Количество переводимых людей ……….……1,50
Время сокращения работы ………………….. 1,00
Для работ (4-7) и 4-5
Введите количество исполнителей
для работ (4-7) 2 <Enter>
для работ 4-5 4 <Enter>
Для работ (4-7) и 4-5
Количество переводимых людей ……………0,46
Время сокращения работы ………………….. 1,48
При переводе 2,606 человек, критический путь
сокращается на 3,184 дней
Будете печатать? 1 – да, 0 – нет <Enter>
5. Составим таблицу резервов работ
| Код работы | Полный резерв Rn(i,j) | Свободный резерв Rc(i,j) | Частный резерв Rч(i,j) | Независимый резерв Rн(i,j) |
| 1-2 | ||||
| 1-3 | ||||
| 2-3 | ||||
| 2-4 | ||||
| 2-5 | ||||
| 3-4 | ||||
| 3-6 | ||||
| 4-5 | ||||
| 4-6 | ||||
| 4-7 | ||||
| 5-7 | ||||
| 6-7 |
Расчет частных резервов ведем по формулам (1.2) или (1.3), расчет независимых резервов ведем по формулам (1.6) или (1.7).
После оптимизации сетевого графика получен следующий результат:
| Работа критического пути | Работа некритического пути | Количество людей, переводимых на работу критического пути | Время, на которое сократится срок выполнения работы критического пути, дни |
| 1-3 | 1-2 | 0,65 | 0,7 |
| 3-4 | 3-6 | 1,5 | |
| 4-7 | 4-5 | 0,46 | 1,48 |
| Итого | 2,61 | 3,18 |
т.е. при переводе 2,6 человек на работы критического пути, он сократится на 3,2 дня.
Содержание отчета по лабораторной работе
1) Таблица исходных данных с рассчитанной продолжительностью каждой работы в днях.
2) Сетевой график с нанесенными на него параметрами событий и работ и выделенным критическим путем.
3) Основные формулы, по которым рассчитывались параметры событий и работ.
4) Линейная диаграмма (график Ганта) с выделенным критическим путем.
5) Результат оптимизации, оформленный в виде таблицы.