Методические указания

Некоммерческое акционерное общество

Алматинский университет энергетики и связи

Факультет аэрокосмических и информационных технологий

Кафедра электроники

 

ТЕХНОЛОГИЯ МАТЕРИАЛОВ И ИЗДЕЛИЙ

ЭЛЕКТРОННОЙ ТЕХНИКИ

Методические указания к выполнению расчетно-графических работ

для студентов всех форм обучения специальности

5В071600 - Приборостроение

 

Алматы 2014

 

 

СОСТАВИТЕЛЬ: Туякбаев А.А. Технология материалов и изделий электронной техники. Методические указания к выполнению расчетно-графических работ и контрольные задания для студентов всех форм обучения специальности 5В071600 – Приборостроение. - Алматы: АУЭС, 2014.- 15 с.

Методические указания содержат основные требования к выполнению расчетно-графических работ.

РГР №1

Рассчитать профиль легирования примесей эпитаксиально-планарных транзисторов для исходных данных, определяемых по последней цифре зачетной книжки (табл.1).

Таблица 1

№ варианта	Темп. загонки бора в оС	Время загонки бора в мин.	Темп. разгонки бора в оС	Время разгонки бора в мин.	Темп. загонки фосфора в оС	Время загонки фосфора в мин.	Темп. разгонки фосфора в оС	Время разгонки фосфора в мин.

 

Построить на миллиметровой бумаге или с помощью компьютера рассчитанный профиль легирования эпитаксиально-планарного транзистора.

Примечание: недостающие для расчета параметры из справочных данных выбираются студентом самостоятельно.

 

Методические указания

Современные твердотельные интегральные транзисторы изго­тавливаются методами планарной или изопланарной технологий, часто с использованием и лучевых технологий [2, 3] . Современные транзисторы характеризуются тем, что области базы и эмиттера получают последовательной направленной локальной диффузией (обычно бора и фо­сфора соответственно) на эпитаксиально выращенный на подлож­ке кремниевый коллекторный слой n - типа. Благодаря большей простоте производства в интегральной схемотехнике преобладаю­щее распространение получили транзисторы типа n-р-n по сравнению с р-n-р транзисторами.

Исходным материалом при изготовлении планарного транзис­тора служит кремниевая подложка с выращенной на ней эпитаксиальной пленкой n - кремния - для транзистора с высокоомным коллектором, либо n – n⁺ - структуры - для транзисто­ров с низкоомным коллектором [1, 2, 3, 4] . Наибольшее распространение при выращивании эпитаксиальных пленок получи­ли методы водородного восстановления трихлорсилана, водород­ного восстановления тетрахлорида кремния и термического разложения моносилана [3]. Низкие скорости выращивания эпитак­сиальных пленок обеспечивают равномерную концентрацию приме­сей в коллекторе транзистора. После этого происходит маскировка окисной пленкой и полу­чение на ней вытравленных окон, в которые при высокой темпе­ратуре осуществляется направленная диффузия акцепторных при­месей (например, бора) для создания базовой области. Диффу­зия бора обычно протекает в две стадии. Первая стадия диффузии (за­гонка) ведется при температуре (900 - 1050°С) в течение от минут до 1 часа. При этом создается большая поверхностная концентрация атомов бора на поверхности кремния, близкая к предельной растворимости бора в кремнии при температуре диф­фузии.

После загонки бора пленку боросиликатного стекла снимают в растворе на основе плавиковой кислоты, пластины промывают в деионизованыой воде и загружают в печь для проведения вто­рой стадии диффузии - перераспределения примесей одновременно с окислением (разгонка).

Разгонка бора проводится при температуре (1050 - 1250°С) в течение нескольких часов (от двух и более). При этом весь процесс протекает в окислительной среде, т.е. используется кислородная атмосфера с увлажнением и без увлажнения.

Поверхность, на которой эпитаксиальная донорная концен­трация равна диффузионной акцепторной концентрации называет­ся металлургической границей коллекторного р-n перехода

N_DK (x_ко) – N_A (x_ко) = 0 . (1)

После этого производится вторая фотолитографическая обработка, при которой локализуются будущие эмиттерные области. В полученные окна проводят диффузию фосфора. При изготовлении высокочастотных транзисторов диффузия фосфора также осуществляется в две стадии. Загонка проводится при температуре (870 - 1150°С), а разгонка при (1000 - 1150°С).

При этом следует отметить, что для каждого конкретного типа транзистора диффузионные температурные режимы задаются с точностью ±1°С . Временные режимы должны быть также доста­точно точны для получения хорошей воспроизводимости.

Металлургической границей эмиттерного р-n перехода x_эо будет поверхность, на которой диффузионная донорная концен­трация равна диффузионной акцепторной концентрации [5]

N_DЭ (x_эо) – N_A (x_эо) = 0 . (2)

Строго говоря, при точном определении металлургической границы эмиттерного р-n перехода x_эо необходимо учитывать и эпитаксиальную донорную концентрацию коллектора, т.е. вместо (2) пользоваться выражением

N_DЭ (x_ко ) – N_A (x_эо ) + N_DK = 0 , (3)

а при определении металлургической границы коллекторного р-n перехода учитывать диффузионную составляющую донорной концентрации примеси

N_DЭ (x_ко ) + N_DK – N_A (x_ко ) = 0 . (4)

Рассмотрим теперь распределение концентрации диффузионных примесей. Общеизвестно, что концентрация диффузионных примесей уменьшается по мере удаления от поверхности [2, 4 - 9] .

Для анализа распределения диффузионной концентрации (диф­фузионного профиля) необходимо решить дифференциальное урав­нение, называемое вторым законом Фика [5, 10]

= D , (5)

где зависимость коэффициента диффузии D от температуры определяется из выражения

D = D_o exp (– ) . (6)

где ΔH – энергия активации; К – постоянная Больцмана; Т – абсолютная температура; D_o – постоянная, зависящая от вида полупроводникового материала и диффузанта.

Значения ΔH и D_o определяются экспериментально и приве­дены в [5, 10, 11]

Общее решение уравнения (5) имеет вид [5]

N(x,t) = 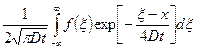, (7)

где - текущая координата интегрирования;

f( ) - начальное распределение концентраций, равное: N(x, 0).

Наибольший практический интерес представляют два частных случая этого решения, которые могут характеризовать две ста­дии диффузии, применяемые в планарной технологии изготовле­ния транзисторов.

Первый случай, соответствующий "загонке" примеси, пред­ставляет собой диффузию от поверхности постоянной концентра­ции: обычно в литературе его называют случаем диффузии из бесконечного источника [5, 12] . Граничные условия в этом случае имеют вид N(0,t) = N_s . Начальная концентрация во всем теле равна нулю. Решение задачи в этом случае для полу­ограниченного тела принимает вид [5]

N(x,t) = N_s erfc 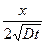, (8)

где erfc(х/(2•√D•t)) = 1 – – дополнительная функция ошибок.

Рассмотренный пример реализуется при больших глубинах диффузии и малых поверхностных концентрациях, когда коэффи­циент диффузии не зависит от концентрации и, следовательно, от координаты х . В работе [5] показано, что при поверх­ностных концентрациях бора менее 6 • 10¹⁹ см^-3 распределение бора при диффузии подчиняется закону дополнительной функции ошибок (8). При N_s > 6•I0¹⁹см^-3 коэффициент диффузии D становится непостоянным и растет, что приводит к по­явлению участка с почти постоянной концентрацией на кривых N = N(x).

Во многих практических случаях важно знать количество диффузанта, проникшего в тело за время диффузии. Эта величина может быть определена по формуле [12]

Q = ∫ j(0,t) dt ,

где j(0,t) – поток диффузанта в объем тела, равный

j(0,t) = N_s•(D/(π•t))^½ .

Интегрируя полученное выражение по времени, получим

Q = N_s/(π)^½•(2•(D•t)^½) .

Данное выражение позволяет определять количество диффузанта при загонке примеси.

При разгонке перераспределение примесей можно использовать следующее выражение

N(x,t) = N_s/2•[erf((h – x/(2•(D•t)^½)) + erf((h + x/(2•(D•t)^½))] .

В данном случае диффузия ведется из ограниченного источника диффузанта. Количество диффузанта, равное Q = N_s•h , в процессе диффузии остается неизменным. Происходит перераспределение примеси по объему тела. Если толщину слоя h устремить к нулю, то получим распределение примеси при диффузии из бесконечно тонкого слоя в полуограниченное тело с отражающей границей. Если полагать, что с устремлением h к нулю количество диффузанта Q в слое остается неизменным, то распределение примеси запишется

N(x,t) = Q/(π• D•t)^½•exp(-x²/(4• D•t)).

Данное выражение в достаточной степени точно позволяет рассчитывать профиль легирования примесей при тех или иных технологических режимах. Однако это выражение не учитывает то, что происходит перераспределение примеси между кремнием и окисным слоем.

Профиль легирования примесей более точно можно рассчитать, используя модель Кейва [13]

N₂(y^*,t) = (1/(2•√π))•N_so•exp[-(y^*+0,22•х_SiO/L₂)²]•[(1/(√gt₂ − y^*) – 1/(2•(√gt₂ − y^*)³) + (√gt₂+c•√D₂•t₂)/(√gt₂−c•√D₂•t₂)•( 1/(√gt₂ + y^*) – 1/(2•(√gt₂ + y^*)³) – (2•c•√D₂•t₂)/(gt₂−c•√D₂•t₂)•(1/(c•√D₂•t₂ + y^*) – 1/(2•(c•√D₂•t₂ + y^*)³)] ,

где y^* = у/(2•√D₂•t₂) ,

L₂ = √D₂•t₂ – диффузионная длина примесей при разгонке;

√gt₂ = (L₂/L₁)•[1−0,22•(х_SiO/L₂)• (L₂/L₁)] ,

c•√D₂•t₂ = (х_SiO/L₂)•K_s•(1−0,22/K_s) ,

L₁ = √D₁•t₁ – диффузионная длина примесей при загонке;

K_s – коэффициент сегрегации, представляющий собой отношение концентрации примеси, внедрившейся в окисел, к концентрации оставшихся примесей в кремнии на границе раздела с окислом, который для бора K_s=3,

N_so = 2•10²⁰см^-3 .

Для определения диффузионных профилей фосфора наиболее точной считается модель Тсай [9] , в которой этот профиль разделяется на три области. Первая состоит из кремния, насыщенного фосфидом кремния и ионизированным фосфором. Толщина этой области х_о определяется временем диффузии

х_о = λ•t ,

где λ – коэффициент пропорциональности, величина которого зависит от температуры и определено было экспериментально.

В таблице 1 приведены значения λ для различных температур диффузии в кремний фосфора.

Таблица 1.

ТоС
λ	1,33•10-5	4,85•10-5	1,03•10-4	1,68•10-4	3,34•10-4	8,34•10-4

 

Вторая область состоит из медленно диффундирующего фосфида кремния, характеризующегося коэффициентом диффузии D_A и быстро диффундирующего фосфора с коэффициентом диффузии D_B . Третья область состоит из быстро диффундирующего фосфора с коэффициентом диффузии D_B . Тогда выражение для концентрации примесей имеет вид

N_s при х < х_о

N(x) = {

N^*(x) при х > х_о ,

где

N^*(x) = (N_s − N_в)/2•exp[−(λ•(x – х_о))/(2•D_A)]•{erfc[(x + х_о)/(2•√D_A•t)] +

erfc[(x − 3х_о)/(2•√D_A•t)]} + N_в/2•exp[−(λ•(x – х_о))/(2•D_B)]•

{erfc[(x − х_о)/(2•√D_B•t)] + erfc[(x − 3х_о)/(2•√D_B•t)]} .

 

За N_В обозначена концентрация быстро диффундирующего фосфора на удалении х_о от поверхности кристалла. Значения N_в , N_s , D_A , D_B были определены Тсай для различных температур диффузии. Для поверхностной концентрации N_s = 4•10²⁰см^-3 в таблице 2 приведены значения N_в , D_A , D_B в зависимости от температуры диффузии Т^оК .

Таблица 2.

ТоК
Nв = 1019 см-3		3,5
DA = 10-16 см2/сек
DB = 10-15 см2/сек

 

Таким образом, эти модели Тсай позволяют определять диффузионный профиль фосфора при процессе загонки. При процессе разгонки перераспределение фосфора можно определять также, как и в случае с бором, только значение коэффициента сегрегации K_s принимать равным 0,1 ÷ 0,001 [5] .

Примерный профиль легирования эпитаксиально-планарного n-p-n транзистора приведен на рис.1. За x_m обозначен максимум результирующей концентрации в базе р–типа. Он находится из условия

(9)

За x' и x'' обозначены границы эмиттерного р-п перехода с квазинейтральными слоями эмиттера и базы. За x'_к и x''_к обозначены границы коллекторного перехода с квазинейтральными слоями базы и коллектора соответственно. Для расчета этих границ можно воспользоваться соотношениями [5, 17, 18]

x_ко – x'_к = L_A ln , (10)

где Δφ_ok - контактная разность потенциалов коллекторного пе­рехода, которая

определяется из соотношения

Δφ_ok = φ_т ln 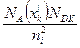, (11)

U_k - напряжение на коллекторном переходе;

L_A - характеристическая длина в распределении акцеп­торов, которая

находится из соотношения

L_A = , (12)

ω_бо – металлургическая толщина базы

ω_бо = х_ко – х_эо , (13)

ε – диэлектрическая постоянная для кремния ε = 12 .

ε_о – диэлектрическая проницаемость вакуума

ε_о = 8,85 ·10^-14 Ф/см .

 

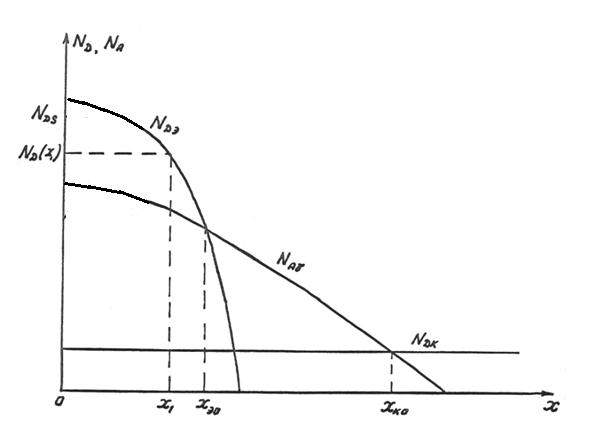
Рис.1. Результирующий диффузионный профиль эпитаксиально-планарного транзистора.

 

Значение толщины коллекторного перехода при обратных смещениях находится из выражения [5]:

x_к^′′ − х_к^′ = L_кр-n = L_A + . (14)

Так как эмиттерный переход при прямых смещениях можно считать плавным, то можно записать для толщины эмиттерного перехода [5,12]

x_э^′′ − х_э^′ = L_эр-n = , (15)

x_э^′′ − х_эо = 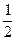L_эр-n ,

где u_э – напряжение на эмиттерном переходе;

– контактная разность потенциалов эмиттерного пе­рехода, которая определяется из соотношения

= , (16)

где p_p(x_э^′′) = N_A(x_э^′′) – N_D(x_э^′′) ,

n_n(х_э^′) = N_D(х_э^′) – N_A(х_э^′).

В активном инверсном включении коллекторный переход находится в прямом смещении, а эмиттерный – в обратном. В этом случае коллекторный переход можно считать плавным и ширину перехода рассчитывать по формуле

x_к^′′ − х_к^′ = L_кр-n = , (17)

а эмиттерный переход резким [39]

x_э^′′ − х_э^′ = L_эр-n = , (18)

x_э^′′ − х_эо = L_эр-n• , (19)

где n_noэ – среднее значение равновесной концентрации основ­ных носителей в эмиттере;

р_роб – среднее значение равновесной концентрации основ­ных носителей в базе.

 

 

РГР №2

Рассчитать электрическое поле в базе эпитаксиально-планарных

транзисторов по данным, полученным в РГР №1.

Методика расчета электрического поля в базе

эпитаксиально-планарных транзисторов

 

В результате диффузии распределение результирующей кон­центрации примесей имеет вид, представленный на рис.1. Вследствие этого дырки в базе будут диффундировать из области с повышенным распределением акцепторов (х = х_m) к обоим р-n переходам. У металлургических границ обоих р-n пе­реходов появится избыточный объемный положительный заряд, а при (х=х_m) появится избыточный объемный отрицательный заряд. Таким образом при отсутствии смещений на обоих р-n переходах в базе образуется внутреннее электрическое поле.

Как видно из рис.1 для нормального активного режима транзистора электрическое поле в базе на участке (х_эо, х_m) является тормозящим для неосновных носителей - электронов, инжектированных в базу из эмиттера, а на участке (х_m, х_ко) - ускоряющим. Для повышения эффективности работы транзистора стремятся уменьшить тормозящий участок поля. На практике обычно (х_m– х_эо)/ω_бо = 0,08 – 0,15 по результатам работ Редди [19]. Для инверсного включения получим, что на участке (х_m, х_ко) электрическое поле для неосновных носителей - электронов, инжектированных в базу из коллектора является тормо­зящим, а на участке (х_m, х_эо) – ускоряющим. Таким образом, при работе в нормальном активном включении ускоряющее электричес­кое поле в базе действует на большем участке, чем тормозящее, а при инверсном включении наблюдается обратный эффект.

Исследованию влияния электрического поля в базе на процессы переноса носителей посвящено много работ [5, 20, 22, 23]. Напряженность поля на участке (х_m, х_ко) оказывается непостоянной: она почти линейно возрастает от эмиттера к коллектору

E_o(x) = E_oэm [1 – (x – х_m)/(2L_D)] , (1)

где Е _oэm - напряженность поля в базе у эмиттерного перехода у точки х_m ;

L_D - длина диффузии примесей.

В работе [22] показано, что значения параметров тран­зистора, полученные при точных расчетах напряженности поля в базе, мало отличаются от значений параметров, полученных при использовании среднего значения напряженности поля в базе, которое получается при допущении, что примеси в базе распределяются по экспоненциальному закону

E_o ≈ φ_т = 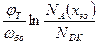. (2)

 

Литература

1. Линн Д., Мейер Ч., Гамильтон Д. Анализ и расчет интегральных схем. Перевод с англ., изд-во "Мир", Москва, 1969 г.

2. Основы технологии кремниевых интегральных схем. Окисле­ние, диффузия, эпитаксия. Под ред. Бургера Р., Донована Р. Перевод с англ. под ред. Мордковича. В.Н., Пресса Ф.П., Москва, "Мир", 1969 г.

3. Алексеенко А.Г. Основы микросхемотехники. Москва, Изд-во "Советское радио", 1971 г.

4. Dobkin R.C. New Developments in monolithic Op Amps. – «Electronics World», 1970, vol.84, №1, p. 45-48.

5. Кремниевые планарные транзисторы. Под, ред. Федотова Я.А Москва, "Советское радио", 1973 г.

6. Зи С.М. Физика полупроводниковых приборов. Перевод с англ. под ред. Трутко А.Ф. Москва, "Энергия", 1973 г.

7. Мэдленд Г.Р., Дикеи Г.К., Ричардсон Р.Д., Боуер Ф.Т., Крет Д„Г. Интегральные схемы. Основы проектирования и техноло­гии. Перевод с англ. под ред. Мартюшова К.Н., Москва, Изд-во "Советское радио", 1970 г.

8. Ргitchord R.L. Electrical Characteristics of transistors. Mc. Graw – Hill Book Company. New york, 1967.

9. Tcaй К. Неглубокие диффузионные слои фосфора в кремнии. "ТИИЭР", 1969 г., т. 57, № 9. стр. 38 - 46.

10. Fuller C.S., Ditzenberger J.A. Diffusion of Donor and acceptor elements in silicon. – «Journal of applied physics». 1956, vol. 27, N5, p.544-553.

11. Fuller C.S., Ditzenberger J.A. Diffusion of boron and phosphorus into silicon. – «Journal of applied physics». 1954, vol. 25, N11, p.1439-1440.

12. Новиков Б.В. Теоретические основы микроэлектроники.

ИЗД-во "Высшая школа", Москва, 1972 г.

13. Cave K.I.S. The base diffusion prodile arising from boron redistribution in the oxide – a useful approximation. – «Solid state Electronics», 1965, vol.8, N12, p.991-993.

14. Chang J.J. Consentration – dependent diffusion of Boron and phosphorus in silicon. – «IEEE Transactions on Electron Devices», 1963, vol.ED-10, N6, p.357-359.

15. Kato T., Nishi Y. Redistribution of diffused boron in silicon by thermal oxidation. – «Japanese journal of applied physics», 1967, vol.3, N7, p.377-383.

16. Chen W.H., Chen W.S. Impurity redistribution in a semiconductor during thermal oxidation, – «Journal of Electrochemical Society», 1967, vol.114, N12, p.1297-1303.

18. Пикус Г.E.Основы теории полупроводниковых приборов. Москва, Изд-во "Наука", 1965 г.

19. Колосов А.А., Горбунов Ю.Н., Наумов Ю.Е. Полупроводнико­вые твердые схемы. Москва, Изд-во "Советское радио", 1965 г.

20. Reddy V.G.K. Influence of surface conditions on silicon planar transistor current gain. – «Solid state Electronics», 1967, vol.10, N4, p.305-334.

21. Болтакс Б.И. Диффузия в полупроводниках. Москва, Физматгиз, 1961.

22. Спиридонов Н.С. Основы теории транзисторов» изд-во "Техника", Киев, 1975 г.

23. Галицкий В.В. Переходные характеристики транзистора с изменяющимся вдоль базы электрическим полем. М.:-Известия вузов. Радиотехника», 1964 г, стр. 472 - 479.