Исследование ВЗАИМОСВЯЗИ МЕХАНИЧЕСКИХ СВОЙСТВ СПЛАВОВ МЕТОДОМ КОРРЕЛЯЦИОННОГО АНАЛИЗА
Методические указания к учебно-исследовательской работе
РПК
«Политехник»
Волгоград
УДК 669.012.2
Р е ц е н з е н т:
канд. техн. наук доцент Приходьков К.В.
Печатается по решению редакционно-издательского совета
Волгоградского государственного технического университета
Исследованиевзаимосвязи механических свойств сплавов методом корреляционного анализа: метод. указания к учебно-исследовательской работе / Сост. А. В. Крохалев, Е. А. Косова / ВолгГТУ. – Волгоград, 2009. – 12 с.
Методические указания содержат изложение основ корреляционного анализа для решения металловедческих задач с применением ПК.
Методические указания предназначены для студентов очной и очно-заочной формы обучения направления 150100 «Металлургия» и специальности 150105 «Металловедение и термическая обработка металлов»
© Волгоградский государственный
технический университет, 2009
1 ЦЕЛЬ РАБОТЫ
Целью лабораторной работы является изучение методики корреляционного анализа и приобретение навыков его практических использования для анализа с помощью ПК массивов данных пассивного эксперимента в металловедении.
2 СОДЕРЖАНИЕ РАБОТЫ
2.1 Изучение методики корреляционного анализа.
2.2 Проведение корреляционного анализа массива данных по механическим свойствам стали после закалки и отпуска при различных температурах с помощью ПК.
2.3 Построение графа корреляционных связей между механическими свойствами стали.
2.4 Разработка схемы расчетного предсказания свойств стали.
3 ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Механические свойства сталей и сплавов, определяющие их работоспособность в тех или иных условиях эксплуатации, характеризуют самыми различными параметрами. Наиболее распространенными из них являются: предел прочности sВ, предел текучести s0,2, относительное удлинение d5, относительное сужение y, ударная вязкость KCU или KCV, твердость HB, HRC или HV.
Характер изменения этих параметров при изменении режимов термической обработки или состава сплава в общем случае также может быть самым разнообразным. Так, например, при увеличении температуры отпуска закаленной от 850 0С в масле стали 38Х2Н2МА происходит уменьшение sВ, s0,2, HRC и увеличение d5, y, KCU (таблица 1).
Таблица 1 – Механические свойства стали 38Х2Н2МА после закалки и отпуска
| Температура отпуска, 0С | s0,2 | sВ | d5 | y | KCU, Дж/см2 | HRC |
| МПа | % | |||||
| y1 | y2 | y3 | y4 | y5 | y6 | |
Определение всех механических характеристик сталей при отработке технологии термической обработки или при контроле ее соблюдения требует значительных затрат времени и материальных средств. Поэтому возникает необходимость отыскания статистически значимых связей между свойствами сплавов, позволяющих расчетным путем предсказывать значения хотя бы части из них.
Чаще всего для решения этой задачи используют корреляционный анализ, суть которого состоит в определении коэффициентов парной корреляции между каждыми двумя из исследуемых параметров.
Коэффициент парной корреляции является мерой тесноты линейной связи между двумя случайными величинами. В общем случае его величина может меняться от 0 до ± 1. Если коэффициент корреляции равен 0, то связь либо вообще отсутствует, либо отлична от линейной. Если он равен ± 1, то связь является линейной функциональной. Чем ближе величина коэффициента корреляции к ± 1, тем связь между величинами сильнее. Знак коэффициента корреляции указывает на направление связи: увеличение одной из переменных при положительной корреляции влечет за собой увеличение, а при отрицательной корреляции – уменьшение другой.
При наличии высокой корреляции между параметрами любой из них может быть исключен из экспериментального определения, т.к. его можно рассчитать по значению другого, используя линейное уравнение регрессии
(3.1)
где 
, 
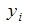- исследуемые характеристики сплава.
Как правило, исключают те параметры, которые методически труднее определить экспериментально или физический смысл которых менее ясен. При этом необходимо помнить, что корреляционные связи в большинстве случаев не являются причинными, т.е. попытка найти прямую связь между, например, относительным удлинением d5 и ударной вязкостью KCU может оказаться бесплодной, так как скорее всего оба эти свойства зависят не прямо друг от друга, а через какой-то другой фактор. Важно лишь то, что по значению одного из них можно оценить уровень другого.
4 МЕТОДИКА РАСЧЕТА С ИСПОЛЬЗОВАНИЕМ МЕТОДА КОРРЕЛЯЦИОННОГО АНАЛИЗА
Для примера расчета значений коэффициентов парной корреляции за основу возьмем данные таблицы 1 и для каждого исследуемого свойства подсчитаем суммы 
, 
, а для каждой пары свойств – сумму 
(N – опытов). Тогда коэффициенты парной корреляции между свойствами находятся по формуле
(4.1)
Количество расчетов можно уменьшить, если принять во внимание, что
(4.2)
и 
. (4.3.)
Результаты расчетов сводим в таблицу, в которой столбцы соответствуют свойствами yi, а строки – свойствам yj, а клетки – коэффициентам корреляции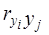 
. Такая таблица является симметричной относительно диагонали, так как соблюдается условие (4.3), и имеет диагональные элементы, равные 1, так как соблюдается условие (4.2).
Таблица 2 – Коэффициенты корреляции между механическими свойствами стали 38Х2Н2МА
| Механические свойства | yi | |||||||
| s0,2 | sВ | d5 | y | KCU | HRC | |||
| y1 | y2 | y3 | y4 | y5 | y6 | |||
| yj | s0,2 | y1 | 0,9825 | -0,93298 | -0,9655 | -0,9465 | 0,9934 | |
| sВ | y2 | 0,9825 | -0,8642 | -0,9281 | -0,8749 | 0,9970 | ||
| d5 | y3 | -0,9398 | -0,8642 | 0,9869 | 0,9902 | -0,8975 | ||
| y | y4 | -0,9655 | -0,9281 | 0,9869 | 0,9747 | -0,9504 | ||
| KCU | y5 | -0,9465 | -0,8749 | 0,9902 | 0,9744 | -0,9083 | ||
| HRC | y6 | 0,9934 | 0,9970 | -0,8975 | -0,9504 | -0,9083 |
После подсчета коэффициентов парной корреляции устанавливаем их статистическую значимость (проверяем статистическую значимость отличия вычисленного коэффициента корреляции от нуля). Для этого выбираем определенный уровень значимости a( обычно это 0,9 или 0,95 или 0,99), находим число степеней свободы f = N – 2 и, используя таблицу 3, находим критическое значение коэффициента корреляции rкр (a, f)
Таблица 3 – Критические значения коэффициентов корреляции
| f | a | ||
| 0,1 | 0,05 | 0,01 | |
| 0,988 0,900 0,805 0,729 0,669 | 0,997 0,950 0,878 0,811 0,754 | 1,000 0,999 0,992 0,974 0,951 |
Найденный по экспериментальным данным коэффициент корреляции считается статистически значимым, если соблюдается следующее условие
(4.4)
Так, например, при a = 0,01 и f = 5 – 2 = 3 
и таблица 2 преобразуется к виду
Таблица 4 - Статистически значимые коэффициенты корреляции между механическими свойствами стали 38Х2Н2МА
| Механические свойства | yi | |||||||
| s0,2 | sВ | d5 | y | KCU | HRC | |||
| y1 | y2 | y3 | y4 | y5 | y6 | |||
| yj | s0,2 | y1 | 0,982 | -0,966 | 0,993 | |||
| sВ | y2 | 0,982 | 0,997 | |||||
| d5 | y3 | 0,986 | 0,990 | |||||
| y | y4 | -0,966 | 0,986 | 0,974 | -0,951 | |||
| KCU | y5 | 0,990 | 0,974 | |||||
| HRC | y6 | 0,993 | 0,997 | -0,951 |
В представленной таблице 4 была произведена замена значений коэффициентов корреляции 
, не отвечающих условию (4.4) и, следовательно, признаваемых статистически не значимыми, на ноль. При этом вероятность ошибки не превышает 1 %. После установления статистически значимых корреляционных связей между каждой парой исследуемых механических свойств переходим к построению уравнений регрессии (3.1), коэффициенты которых подсчитываем по формулам
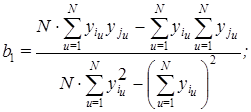(4.5)
(4.6)
Для данных таблицы 4 эти расчеты дают:
y1=222+0,738y2 (4.7 )
y1=2773-29,3y4 (4.8)
y1=-57,82+30,2y6 (4.9)
y2=-241+1,31y1 (4.10)
y2=-354+40,4y6 (4.11)
y3=-5,91+0,354y4 (4.12)
y3=7,69+0,069y5 (4.13)
y4=91,6-0,032y1 (4.14)
y4=17,6+2,75y3 (4.15)
y4=38,8+0,19y5 (4.16)
y5=-107+14.1y3 (4.17)
y5=-190+4,99y4 (4.18)
y6=2,46+0,033y1 (4.19)
y6=8,99+0,025y2 (4.20)
Полученные уравнения (4.7) - (4.20) могут быть использованы для расчетного предсказания свойств стали 38Х2Н2МА.
С целью минимизации числа механических характеристик, которые необходимо определять экспериментально, чтобы затем по полученным уравнениям регрессии оценить весь комплекс механических свойств, нужно построить и проанализировать граф корреляционных связей.
Для этого рассматриваемые свойства изображают в виде точек (вершин графа) и соединяют отрезками прямых линий те из них, между которыми существует статистически значимые корреляционные связи (строят ребра графа). Пример такого построения, отвечающий данным таблицы 4, приведен на рисунке 1
 |
Рисунок 1- Граф корреляционных связей между механическими свойствами стали 38Х2Н2МА
Основываясь на графе, разрабатывают схему предсказания свойств исследуемого сплава по одному или нескольким, выбранным в качестве основных, свойствам. При этом в качестве основных характеристик чаще всего выбирают те, которые имеют наибольшее число связей с другими характеристиками и наиболее просто определяются экспериментально. В нашем случае в качестве такого свойства может выступать твердость HRC. Данный параметр незначительно (всего лишь на единицу) уступает по количеству связей с другими свойствами самой влиятельной в нашем случае характеристике – относительному сужению ψ.
Схему предсказания свойств сопровождают списком линейных уравнений регрессии, выбранных из общего набора построенных уравнений ((4.7)-(4.20)). Уравнения нумеруют по порядку римскими цифрами и присвоенные им номера для наглядности наносят на схему предсказания. Схема предсказания свойств, входящих в граф, приведенный на рисунке 1, представлена на рисунке 2.
|
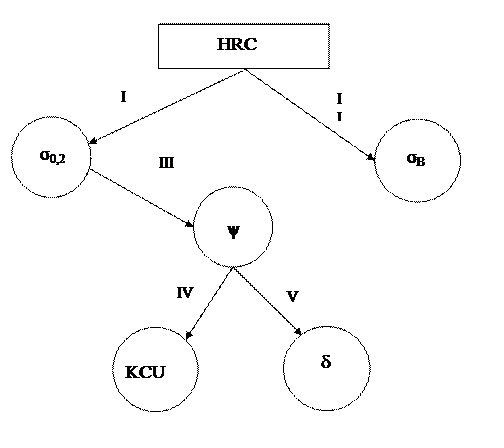
I – σ0,2 = - 57,82 + 30,2 . HRC
II – σВ = - 354 + 40,4 . HRC
III – ψ = 91,6 - 0,032 . σ0,2
IV – KCU = - 190 + 4,99 . ψ
V – δ5 = - 5,91 + 0,354 . ψ
Рисунок 2 – Схема предсказания свойств стали 30Х2Н2МА
5 ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Получить индивидуальное задание, привести краткое описание методики корреляционного анализа и подготовить данные для ввода в ПК. По полученным уравнениям регрессии оценить весь комплекс механических свойств путем построения и анализа графа корреляционных связей между
механическими свойствами сплава, представленного в индивидуальном задании. Основываясь на графе, разработать схему предсказания свойств исследуемого сплава. По полученным в ходе работы данным сделать вывод о взаимосвязи механических свойств рассмотренной марки стали и возможности расчетного предсказания их значений.
6 КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Для каких целей может быть использован корреляционный анализ?
2. Какие значения могут принимать коэффициенты парной корреляции? Что они означают?
3. Как вычисляются коэффициенты парной корреляции между свойствами стали или сплава?
4. Как оценивается статистическая значимость коэффициентов парной корреляции?
5. Как построить уравнения регрессии между закоррелированными параметрами?
6. С какой целью и каким образом строится граф корреляционных связей?
7. Как строится схема расчетного предсказания свойств сталей или сплавов?
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
1.Ахназарова С.Л., Кафаров В.В. Оптимизация эксперимента в химии и химической технологии – М.: Высшая школа, 1978 – 319 с.
2.Новак Ф. С., Арсов Я.Б. Оптимизация процессов технологии металлов методами планирования экспериментов – М.:Машиностроение, 1980 – 304 с
Александр Васильевич Крохалев
Елена Аркадиевна Косова