Анализ качества полученной модели.

Оценка значений параметров парной линейной регрессии.

Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК). Сущность метода МНК состоит в поиске линейной функции, которая минимизирует сумму квадратов отклонений фактических (наблюдаемых) значений от расчетных (модельных):

.

Используя методы дифференциального исчисления можно доказать, что оценки параметров парной линейной регрессии могут быть получены из системы линейных уравнений:

Параметры уравнения регрессии определяются формулами:

.

Анализ качества полученной модели.

Если модель хорошо описывает исходные наблюдения, то между фактическими значениями результирующего признака и соответствующими теоретическими значениями, найденными по уравнению регрессии, должна существовать тесная зависимость. Ее можно оценить коэффициентом корреляции:

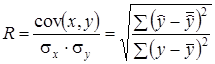
Если значение коэффициента корреляции близко к единице, это свидетельствует о высоком качестве модели. Квадрат коэффициента корреляции называется коэффициен­том детерминации R². Он показывает удельный вес вариации результирующего признака, которую объясняет уравнение регрессии, в его общей вариации.

Еще одним критерием качества выступают отклонения и, и их дисперсия. Существует два пути рассмотрения отклонений, полученных в результате оценивания уравнения регрессии. С одной стороны, чем больше остатки, тем хуже регрессия и тем меньше коэффициент корреляции. Однако остатки, рассматриваемые по отдельности, указывают, когда и в какой степени построенная модель не смогла объяснить фактические данные. Извлечение пользы из такого анализа требует от исследователя большого терпения. Если выборка достаточно мала, то вам следует очень внимательно рассмотреть каждое наблюдение с большим отри­цательным или положительным отклонением и попытаться най­ти для них гипотетическое объяснение. Если вам удастся вы­явить закономерность в отклонениях по нескольким наблюдени­ям, то это большой шаг вперед. Следующим шагом должно быть нахождение разумного способа для количественного описания данного фактора и включения его в модель.

Дополнительными критериями адекватности полученной мо­дели является оценка значимости (существенности) уравнения регрессии в целом и отдельных его параметров. Оценка значи­мости уравнения регрессии в целом проводится с помощью F-критерия, а оценка статистической значимости параметров мо­дели предполагает использование t-критерия.