Раздел 2. Фундаменты в открытых котлованах на естественном основании (фундаменты мелкого заложения).
Фундаменты мелкого заложения (ФМЗ):
1) глубина заложения  ;
;
2) возводятся в предварительно открытых котлованах;
3) засыпка пазух грунтом с уплотнением
4) при расчёте не учитывают сопротивление грунта по боковой поверхности.
2.1. Классификация ФМЗ.
1) по материалу:
а) железобетонные;
б) бетонные;
в) бутобетонные;
г) бутовые;
д) кирпичные;
2) по конструкции:
а) ленточные фундаменты под стены зданий или под ряд колонн;
б) отдельные (столбчатые) фундаменты под стойки и колонны
сооружений;
в) сплошные фундаменты под всем сооружением в виде железо
бетонных плит под сетку колонн или стены:
− плиты сплошного сечения;
− плиты коробчатого сечения;
г) массивные фундаменты – в виде массива под всем небольшим
в плане сооружением (дымовая труба, доменная печь, мостовая
опора).
3) по индустриальности изготовления (степени сборности)
а) сборные фундаменты;
б) монолитные фундаменты;
в) сборномонолитные фундаменты;
4) по характеру работы материала
 |
Рис. 3. Схемы фундаментов: а) жёсткий; б) гибкий; αy − угол наклона линии
уступов к вертикали; αпр − предельный угол распределения давления в ма -
териале фундамента.
В железобетонных фундаментах нижняя плоская или ступенчатая часть называется плитой, а верхняя – фундаментной стеной у ленточных фундаментов или подколонником у столбчатых фундаментов. Пространство в верхней части подколонников, служащее для установки колонны, называется стаканом.
2.2. Проектирование фундаментов мелкого заложения.
Заключается в выборе типа и материала фундамента, определении его размеров и армирования.
2.2.1. Исходные данные для проектирования ФМЗ:
1) проект надфундаментной части сооружения;
2) данные инженерно-геологических изысканий;
3) данные о климате и гидрологии;
4) данные о действующих нагрузках;
5) топографическая съёмка.
2.2.2. Последовательность проектирования ФМЗ:
1) определение действующих нагрузок;
2) оценка грунтов основания;
3) выбор отметки обреза фундамента;
4) выбор глубины заложения фундамента;
5) определение размеров подошвы фундамента расчётами по
предельным состояниям основания;
6) конструирование и расчёт тела фундамента.
Основными размерами фундамента являются его высота и размеры подошвы в плане.
После определения размеров подошвы производят конструирование жёсткого бетонного фундамента. В результате этого устанавливают детальные размеры фундамента по высоте (его профиль) и определяют армирование железобетонного фундамента.
2.2.3. Оценка грунтов основания
Грунты основания оцениваются по несущей способности (прочности) и сжимаемости.
Несущую способность грунтов оценивают послойно, сверху вниз, по геологическим разрезам или грунтовым колонкам, устанавливая для кровли каждого слоя расчётные сопротивления R грунтов сжатию (СНиП 2.02.01 – 83. Основания зданий и сооружений). Для слоя, залегающего непосредственно у поверхности, расчётные сопротивления первоначально определяют на глубине, соответствующей минимальной глубине заложения фундамента.
Сжимаемость грунтов предварительно оценивается путём анализа значений модулей деформации грунтов Е.
По результатам сравнительного анализа R и E определяется несущий слой и выбирается тип фундамента, а также назначается его глубина заложения.
2.2.4. Выбор отметки обреза фундамента
Отметку обреза фундамента обычно назначают на 15 – 20 см ниже поверхности грунта. Для фундамента, расположенного внутри сооружения, обрез должен быть заглублен ниже уровня пола первого этажа, а для зданий с подвалами – ниже пола подвала.
2.2.5. Выбор глубины заложения фундамента
На выбор глубины заложения фундаментов влияет ряд факторов:
1) учёт глубины промерзания пучинистых грунтов.
При расположении подошвы фундамента в зоне промерзания в случае пучинистых грунтов на фундамент могут действовать силы пучения, нормальные к его подошве и касательные к боковой поверхности. Наибольшую опасность для сооружения представляют нормальные силы пучения. Если эти силы превысят давление на грунт от сооружения, то в процессе промерзания грунтов могут возникнуть значительные и неравномерные подъёмы, а при оттаивании – неравномерные осадки.
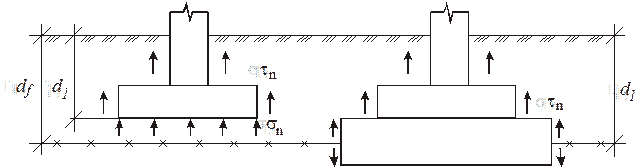
Рис.4. Фундаменты в пучинистых грунтах: df – расчётная глубина промерза−
ния (СНиП 2.02.01 – 83*); d1 – глубина заложения фундамента. 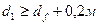
К пучинистым грунтам относятся:
− пески мелкие и пылеватые;
− все пылеватые глинистые грунты;
2) учёт инженерно-геологических условий строительной площадки:
d1 – выбирается в зависимости от прочности и сжимаемости грунтов.

d1 обычно выбирают с
учётом других условий
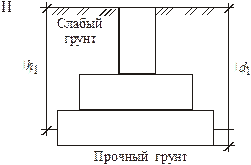
подошву фундамента заглубляют в первый от поверхности прочный грунт.
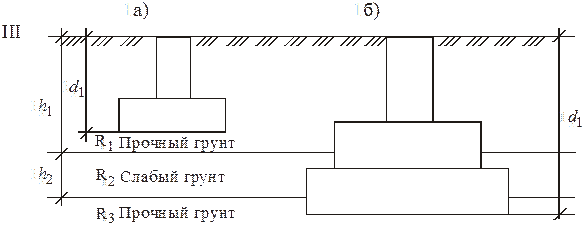 |
а) d1< h1
б) d1> h1 + h2
(б) – абсолютно надёжный способ, но предполагает большой объём земляных работ и большой расход бетона.
В случае (а) необходимо выполнить проверку слабого подстилающего слоя
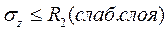 (2.1)
(2.1)
Если условие 2.1 не выполняется, то размеры подошвы фундамента нужно считать из условия на границе слабого слоя, или укреплять слабый слой.
3) учёт конструктивных особенностей:
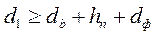 |
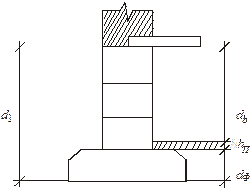
Рис. 5. Фундамент в здании с подвалом: d1 – глубина
заложения фундамента; db – высота подвальной стены;
hn – толщина пола подвала; dф – высота фундаментной
плиты.
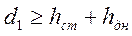 |
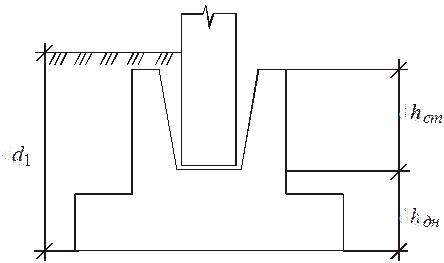
Рис.6. Стаканное сопряжение колонны с фундаментом:
d1 – глубина заложения фундамента; hcm – глубина ста−
кана; hдн – толщина днища стакана.
2.3. Определение размеров подошв фундаментов расчётом по второй группе предельных состояний.
Главным положением при проектировании оснований, т.е. при выборе основных размеров подошвы фундаментов, является ограничение неравномерностей осадок, приводящих к деформации конструкций сооружений.
Ограничение величины неравномерности осадок:
 или
или 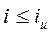 ; (2.2)
; (2.2)
где ΔS – разность между осадками соседних фундаментов, определяемая в т.ч. с учётом фактора времени; L – расстояние между осями рассматриваемых соседних фундаментов; (ΔS/L)u – предельно допустимое значение относительной неравномерности осадки; i – крен сооружения по расчёту; iu – предельно допустимый крен сооружения.
2.4 Расчётное сопротивление грунта.
R – расчётное сопротивление грунта основания, при котором развивающиеся зоны пластических деформаций грунта (зоны местного нарушения устойчивости) незначительно нарушают линейную зависимость между деформациями.
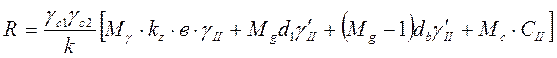
где 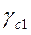 и
и 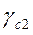 − коэффициенты условий работы соответственно основания и сооружения во взаимодействии с основаниями; k − коэффициент: k = 1, если φII и CII определены испытаниями; k = 1,1, если φII и CII приняты по таблицам;
− коэффициенты условий работы соответственно основания и сооружения во взаимодействии с основаниями; k − коэффициент: k = 1, если φII и CII определены испытаниями; k = 1,1, если φII и CII приняты по таблицам; 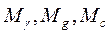 − коэффициенты, зависящие от расчётного значения угла внутреннего трения φII ; kz - коэффициент: kz =1 принимается при в < 10 м; kz = (z0/в) + 0,2 при в > 10 м (здесь z0 = 8 м); в – ширина подошвы фундамента;
− коэффициенты, зависящие от расчётного значения угла внутреннего трения φII ; kz - коэффициент: kz =1 принимается при в < 10 м; kz = (z0/в) + 0,2 при в > 10 м (здесь z0 = 8 м); в – ширина подошвы фундамента;  и
и 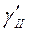 − расчётное значение удельного веса грунтов, залегающих соответственно ниже подошвы фундамента и в пределах глубины заложения фундамента; d1 – глубина заложения фундамента от пола подвала; при отсутствии пола подвала – от планировочной поверхности; db – глубина подвала; CII – расчётное значение удельного сопротивления.
− расчётное значение удельного веса грунтов, залегающих соответственно ниже подошвы фундамента и в пределах глубины заложения фундамента; d1 – глубина заложения фундамента от пола подвала; при отсутствии пола подвала – от планировочной поверхности; db – глубина подвала; CII – расчётное значение удельного сопротивления.
2.5. Определение размеров подошвы центрально нагруженных фундаментов по расчётным сопротивлениям.
2.5.1. Исходная задача

А = а · в −? площадь подошвы фундамента
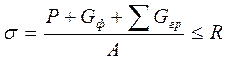 ;
;
 ;
;
где 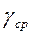 − осреднённый вес грунта и материала фундамента
− осреднённый вес грунта и материала фундамента
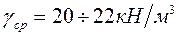 ;
;

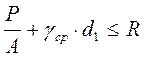
Приводим R к форме удобной для расчёта R = α1 + α2 · в
где 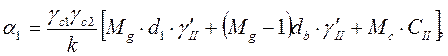
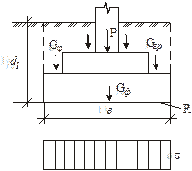
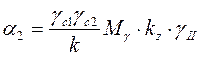


Рис.7. Расчётная схема
2.5.2. Ленточные фундаменты
P' – погонная нагрузка
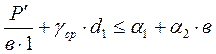 ,
, 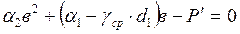

 |
Рис.8. Расчётная схема
 |
2.5.3. Прямоугольные фундаменты
Рис.9. Расчётная схема
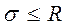 ;
;
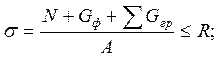


Задаваясь одним из размеров определяем второй:
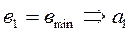 (вmin – из условия размещения несущей надземной конструкции)
(вmin – из условия размещения несущей надземной конструкции)


Из полученных пар размеров подошвы выбираем оптимальный вариант из условия размещения надфундаментной части и CА = Аmin.
2.6. Определение размеров подошвы внецентренно нагруженных фундаментов.
2.6.1. Выбор положения центра подошвы фундамента при внецентренной нагрузке.
При проектировании фундаментов на нескальных грунтах положение равнодействующей нагрузок относительно центра тяжести подошвы фундамента ограничивают условием
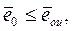 (2.3)
(2.3)
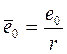 − относительный эксцентриситет,
− относительный эксцентриситет,
 − абсолютный эксцентриситет равнодействующей нагрузок.
− абсолютный эксцентриситет равнодействующей нагрузок.
M – момент относительно главной центральной оси подошвы фундамента,
N – вертикальное усилие на подошву фундамента,
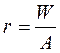 − радиус ядра сечения подошвы фундамента,
− радиус ядра сечения подошвы фундамента,
W – момент сопротивления подошвы фундамента,
А – площадь подошвы фундамента,
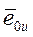 − предельный относительный эксцентриситет
− предельный относительный эксцентриситет
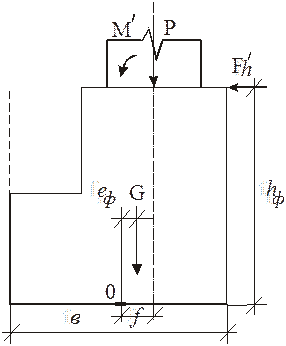 |
Условие (2.3) можно удовлетворить выбором положения центра тяжести подошвы фундамента относительно вертикальной оси несущей конструкции.
Рис.10. Схема к определению положе−
ния центра подошвы фундамента
 (2.4)
(2.4)
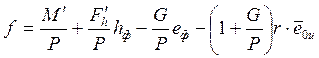
Значение смещения f при котором напряжения под подошвой фундамента будут равномерными, получим приравняв 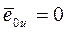 .
.
Также принимаем  , т.к. эта величина очень мала.
, т.к. эта величина очень мала.
При проектировании фундаментов на нескальных грунтах положение центра подошвы фундамента целесообразно определять при действии постоянных нагрузок, т.к. основную долю перемещений фундамента вызывают постоянные нагрузки
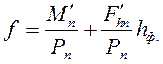
2.6.2. Три расчётных случая при определении размеров подошвы внецентренно нагруженных фундаментов.
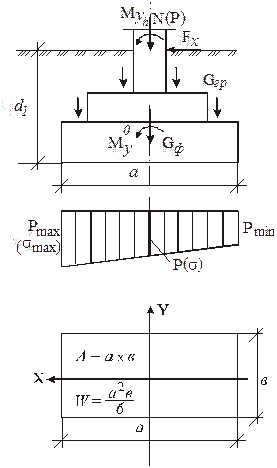
Рис.11. Расчётная схема
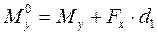
Условия:
1) 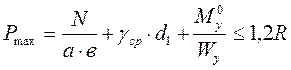
2) 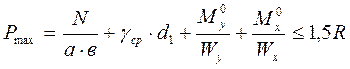
3) 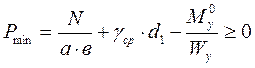
4) 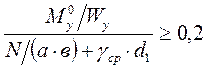

(3) и (4) условия необходимые для того, чтобы классифицировать фундамент по действию нагрузок. Имеются 3 случая загружения фундаментов в зависимости от условий (3) и (4).
1. Случай малых эксцентриситетов. Не выполняется условие (4). Расчёт фундамента ведётся, как центрально нагруженного, без учёта действия момента.
2. Случай средних эксцентриситетов. Одновременно выполняются условия (3) и (4). Размеры подошвы фундамента определяются из условия (1) или (2).
3. Случай больших эксцентриситетов. Не выполняется условие (3). Расчёт ведётся с учётом отрыва подошвы от грунта.
Определение размеров подошвы внецентренно нагруженных фундаментов ведётся в следующей последовательности:
1) размеры определяются как для случая средних эксцентриситетов;
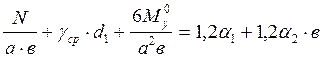



оптимальный вариант выбирают по условию размещения надфундаментной части (должно быть а > в)
2) Затем проверяют условия (3) и (4). Если окажутся случаи малых или больших эксцентриситетов, то размеры уточняются по выражениям, соответствующим этим расчётным случаям.
2.6.3. Расчёт фундаментов в случае частичного отрыва его подошвы от грунта.
 |
Рис.12. Расчётная схема
N – равнодействующая нагрузка
е – эксцентриситет равнодействующ.
В действительности нормальные давления под подошвой фундамента могут быть только сжимающими. В этом случае давления можно определить в предположении их распределения по закону треугольника, из условия, что объём эпюры давлений равен силе N, а центр её тяжести лежит на линии действия этой силы.



 ;
;



2.7. Проверка давления на подстилающий слой грунта.
 |
Рис.13. Схема проверки давления на слабый подстилающий слой.
Если основание – слоистое напластование и R1>>R2, а d1<h1, то необходимо выполнить проверку слабого подстилающего слоя  (слабого слоя).
(слабого слоя).




 ;
;
При расчёте R2 – коэффициенты принимают для слабого слоя. Значения «в» и «d» устанавливают для условного фундамента АВСД, рассеиванием давления в пределах слоя толщиной z.

Площадь условного фундамента
 , N0II – нагрузка, передаваемая конструкциями на обрез фундамента
, N0II – нагрузка, передаваемая конструкциями на обрез фундамента

где a = (l - в)/2 (l и в – размеры подошвы проектируемого фундамента).
2.8. Определение перемещений фундаментов.
2.8.1. Расчёт осадки фундамента методом послойного суммирова-
ния.
 |
Этот метод позволяет учесть неоднородность основания, выра-
Рис.14. Схема к расчёту осадки методом послойного суммирования:
1 – эпюра природного давления; 2 – эпюра дополнительного давле-
ния от сооружения; 3 – эпюра природного давления уменьшенного
в пять раз; 4 – нижняя граница сжимаемой толщи.
жающуюся в изменении модуля деформации по глубине. Метод применим для расчёта осадок фундаментов, имеющих различную форму в плане.
Последовательность расчёта:
1) определяем среднее фактическое напряжение на подошве фундамента

2) определяем осадочное напряжение

3) строим эпюру природного давления грунта

4) разбиваем толщу грунта на элементарные слои мощностью hi

5) определяем напряжения от дополнительных нагрузок по глубине сжимаемой толщи

где 


6) строим эпюру дополнительных давлений
7) определяем положение нижней границы сжимаемой толщи (ВС)

8) определяем величину осадки

9) сравниваем расчётную осадку с предельно допустимой осадкой для данного типа сооружения

10) проверяем относительную разность осадок двух соседних фундаментов


Рис.15. Схема к расчёту относительной
разности осадок
2.8.2. Расчёт осадки методом линейно-деформированного слоя конечной толщины.
Этот метод применяют в двух случаях:
а) если в пределах сжимаемой толщи Hc , установленной, как и в
методе послойного суммирования, находится слой грунта с модулем деформации  мПа и мощностью hc , удовлетворяющей условию
мПа и мощностью hc , удовлетворяющей условию

где Еп – модуль деформации слоя, залегающего ниже слоя с модулем Ес;
б) когда ширина подошвы фундамента  м и модуль деформа-ции грунтов основания
м и модуль деформа-ции грунтов основания  мПа.
мПа.
Величина осадки:

где Р – среднее давление под подошвой фундамента; kc - коэффициент, учитывающий концентрацию напряжений за счёт влияния жёсткого подстилающего слоя; km – коэффициент, учитывающий влияние ширины подошвы фундамента; ki и ki-1 – коэффициенты принимаемые в зависимости от n=a/в и относительных глубин mi=zi/в и mi-1=zi-1/в подошвы и кровли i-го слоя соответственно.

Рис.16. Схема к расчёту осадки методом
линейно-деформированного слоя конеч-
ной толщины: 1 – фундамент; 2 – i-й слой
грунта с модулем деформации Ei; 3 – кро-
вля несжимаемого слоя.
2.8.3. Определение крена фундамента.
Крен отдельного прямоугольного фундамента при действии на него момента М определяется по обобщённой формуле:

где μ – коэффициент поперечного расширения грунта; ke - коэффициент, определяемый по графикам в зависимости от n = а/в и m' = hk/в;
km – коэффициент, принимаемый по таблице в зависимости от значений Е и в; l – сторона подошвы фундамента, в направлении которой действует момент.
2.8.4. Предельно допустимые деформации и перемещения зданий.
Предельно допустимые деформации и перемещения зависят от чувствительности конструкций к неравномерным осадкам и предъявляемых к сооружениям эксплуатационных требований (архитектурный облик, работа транспорта и другого оборудования). Значения Su, ΔSu, iu для некоторых типов сооружений установлены по опыту строительства и приводится в СНиП 2.02.01-83 «Основания зданий и сооружений».
2.9. Расчёт устойчивости фундаментов на сдвиг по подошве.

Рис.17. Расчётная схема фундамента при
значительной горизонтальной составля-
ющей внешней нагрузки
Коэффициент запаса (устойчивости)

где kst,u = γn/γc – предельный коэффициент устойчивости; N0I - вертикальная составляющая расчётной нагрузки на обрез фундамента;
GfgI – расчётный вес фундамента и грунта на уступах; f – расчётный коэффициент трения материала фундамента по грунту; F0hI – расчётная величина горизонтальной составляющей силы, действующей по обрезу фундамента.
Если F0hI >> f(N0I + GfgI), сначала находят необходимый вес фундамента и грунта из выражения

Если F0hI ≈ f(N0I + GfgI), то определяют размеры фундамента как внецентренно загруженного, а затем проверяют на сдвиг.
Если в основании залегает пылевато-глинистый грунт, обладающий сцеплением, но имеющий малый угол внутреннего трения, подошву фундамента иногда выполняют наклонной. При скальном основании подошву делают ступенчатой.

Рис.18. Схемы фундаментов: а.) – при связ-
ном грунте в основании; б.) – при скальном
основании
2.10. Гибкие фундаментные балки и плиты.
Гибкие фундаменты – это те, деформации изгиба которых того же порядка, что и осадки этого же фундамента. Расчёт таких фундаментов проводится с учётом совместной работы конструкции фундамента и грунтового основания. Распределение контактных реактивных давлений считается нелинейным. Линейное распределение давлений используется лишь для предварительного определения сечений конструкций.
При расчёте фундаментных конструкций на упругом основании реальное грунтовое основание представляется в виде механической модели, т.е. вводится гипотеза относительно характера деформирования основания под нагрузкой.
1. Гипотеза коэффициента постели (Фусса – Винклера).
Эта гипотеза предполагает, что осадка какой-либо точки поверхности основания «S» прямо пропорциональна давлению «P», приложенному в той же точке и не зависит от загружения соседних точек основания, т.е. грунт не обладает распределительной способностью.
Механической моделью основания служит набор не связанных между собой пружин (рис.19, а). Деформационные свойства основания описываются коэффициентом постели, не зависящим от размеров загружаемой площадки
С = Р/S
2. Гипотеза упругого полупространства.
Эта гипотеза предполагает, что основание работает как сплошная однородная упругая среда, ограниченная сверху плоскостью и бесконечно простирающаяся вниз и в стороны. Грунт обладает распределительной способностью – вокруг фундамента образуется воронка оседания (распределительная способность преувеличена). (рис. 19, б).
Распределение напряжений в упругой среде описывается формулами теории упругости. Деформационные свойства упругого полупространства характеризуются модулем деформации «Е» и коэффициентом Пуассона «ν».

Рис. 19. Перемещение поверхности основания под нагрузкой: а – по ги-
потезе Винклера; б – по гипотезе упругого полупространства.
В зависимости от условий работы фундаментные конструкции рассчитывают на основе одной из трёх задач теории упругости.
1. Плоская задача. Рассчитываются протяжённые фундаментные конструкции, у которых каждая полоса шириной 1 м, выделенная в поперечном направлении, работает в одинаковых условиях с любой другой аналогичной полосой (рис.20, а). К этому классу относятся ленточные фундаменты под стены зданий, фундаменты сухих доков, протяжённые плиты под сетку колонн и т.д.
2. Осесимметричная задача. Рассчитываются круглые и кольцевые фундаментные плиты. К этому классу относятся фундаментные плиты дымовых труб, водонапорных башен, газгольдеров и т.д. (рис. 20, б).
3. Пространственная задача. Рассчитываются фундаменты, работу которых даже приближённо нельзя описать условиями плоской или осесимметричной задачи. К этому классу относятся фундаменты под колонны в виде одиночных или перекрёстных лент, фундаментные балки, прямоугольные фундаментные плиты и т.д. (рис.20, в,г).

Рис. 20. Различие условий работы конструкций на упругом основании: а – плоская задача; б – осесимметричная задача; в, г - пространственная задача.
Используемые для расчёта фундаментных конструкций методы зависят от принятой механической модели основания и условий работы конструкции (плоская, осесимметричная или пространственная задача). Эти методы разделяются на две группы: 1) методы в которых на основе условий равновесия и условия полного примыкания подошвы балки или плиты к грунту составляются одна или две системы линейных уравнений с несколькими неизвестными; решение этих систем позволяет определить эпюру реактивных давлений, а затем уже и эпюры изгибающих моментов, поперечных сил и прогибов (осадок). (Метод Б.Н.Жемочкина, метод М.И.Горбунова – Посадова); 2) методы, основанные на использовании готовых таблиц всех расчётных величин; такие таблицы составлены для большинства типов конструкций при различной их относительной гибкости, характере и размещении нагрузок.
В случае сложных конструкций, неоднородных грунтовых оснований достаточно точные решения могут быть получены только численными методами с использованием ЭВМ.