Основные понятия по теме
Тема 2 ТЕОРИЯ БОРА ДЛЯ ВОДОРОДОПОДОБНЫХ АТОМНЫХ СИСТЕМ
1 Спектральные серии в спектрах водородоподобных атомов, комбинационный принцип Ритца
2 Постулаты Бора, теория Бора для водородоподобных систем
3 Правила квантования эллиптических орбит Бора-Зоммерфельда
4 Преимущества и недостатки теории Бора
Основные понятия по теме
Водородоподобная атомная система состоит из положительно заряженного ядра с зарядом 
, где 
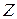– порядковый номер химического элемента в Периодической системе, и одного электрона, движущегося относительно ядра в соответствии с теорией Бора по замкнутой траектории (орбите). Реальными водородоподобными атомными системами являются атом водорода ( 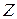=1), однократно ионизированный атом гелия ( 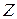=2), двукратно ионизированный атом лития ( 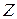=3) и т. д.
Результаты экспериментальных исследований спектров испускания водородоподобных систем были обобщены посредством формулы, по которой можно определить длину волны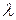 
(или волновое число 
, или частоту 
) любой спектральной линии анализируемых атомных систем:
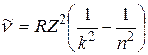. (2.1)
Выражение (2.1) называют обобщенной формулой Бальмера.
Здесь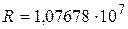 
м-1 – постоянная Ридберга, k = 1, 2, 3, …; n = (k + 1), (k + 2), … .
При k = 1, n = 2, 3, 4, … по формуле (1.1) можно рассчитать волновые числа спектральной серии Лаймана;
при k = 2, n = 3, 4, 5, … – волновые числа серии Бальмера;
при k = 3, n = 4, 5, 6,… – серии Пашена
при k = 4, n = 5, 6, 7, … – серии Брэкета;
при k = 5, n = 6, 7, 8, … – серии Пфунда и т.д.
Спектральная линия k-й серии, волновое число которой определяется в соответствии с формулой (1.1) при 
, называется границей k-й серии; а линия с волновым числом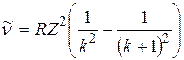 
называется головной линией k-й серии.
Теоретическое обоснование сериальных закономерностей, наблюдаемых в спектрах водородоподобных систем, дано в теории Бора, которая базируется на законах классической механики и квантовых постулатах Бора, согласно которым:
1. Атомы и атомные системы могут длительное время, не излучая и не поглощая энергии, находиться в стационарных состояниях, которым соответствуют значения энергии E1, E2, …, En, …, образующие дискретный ряд.
2. Переходя из стационарного состояния с энергией En в состояние с энергией Ek, атом излучает или поглощает квант электромагнитного излучения, частота которого определяется правилом частот Бора
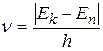, (2.2)
где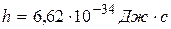 
– постоянная Планка.
Бор в теории для водородоподобных систем рассматривал только круговые орбиты электрона, для которых им сформулировано условие квантования
, (n = 1, 2, 3, …), (2.3)
где 
– масса электрона, 
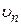– его скорость, 
– радиус 
-й орбиты.
Смысл условия квантования круговых орбит состоит в том, что в атоме реализуются только такие круговые орбиты, при движении по которым электрон имеет момент количества движения, кратный приведенной постоянной Планка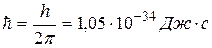 
:
Второй закон Ньютона для электрона, движущегося по n–й круговой орбите, имеет вид:
. (2.4)
где 
, 
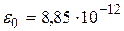Ф/м – диэлектрическая постоянная.
Решив систему уравнений (2.3) и (2.4) относительно радиуса 
и скорости электрона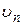 
и выразив полную энергию электрона n –й круговой орбите
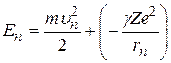, (2.5)
Бор получил формулу
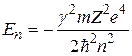. (2.6)
Воспользовавшись правилом частот (2.2) и связью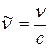 
, он выразил волновое число спектральной линии, обусловленной квантовым переходом атомной системы из n-го стационарного состояния в k-е:
. (2.7)
Как видим, эмпирическое выражение (2.1) для волнового числа спектральной линии и теоретическое (2.7) совпадают, если принять, что
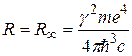. (2.8)
Расчетное значение постоянной Ридберга (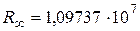 
м-1) хорошо согласуется с экспериментальным ( 
м-1), что является основанием для вывода о правильности предложенной Бором модели. Некоторое отличие этих значений удалось объяснить, введя поправку в полученное решение, учитывающую в атоме наряду с движением электрона и движение ядра, масса которого 
. С формальной точки зрения это означает, что во всех соотношениях теории Бора необходимо заменить массу электрона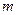 
приведенной массой 
системы, состоящей из ядра и электрона. При этом эмпирическое значение постоянной Ридберга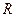 
и теоретическое значение ее 
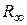связаны следующим образом:
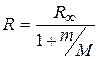. (2.9)
Зависимость постоянной Ридберга от массы ядра обусловливает смещение соответствующих спектральных линий, характерных для различных изотопов данного химического элемента, и называется изотопическим сдвигом.
На рисунке 2.1 приведена схема энергетических уровней и переходов между ними для водородоподобного атома, построенная в результате анализа формул (2.2) и (2.6).
Стационарное состояние с наименьшей энергией ( 
) называется основным, или нормальным, все остальные состояния (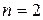 
, 3,…) – возбужденные. При , согласно (2.6), En = 0. При E < 0 электрон связан с ядром и спектр значений его энергий дискретен (энергия квантована); при E > 0 электрон свободен и спектр значений его энергии непрерывен. Переход электрона в области дискретного спектра из одного энергетического состояния в другое, с большей энергией, есть возбуждение атома. При переходе электрона с одного из уровней дискретного спектра в область непрерывного спектра энергий атом превращается в несвязанную систему «положительный ион + электрон», то есть происходит его ионизация.
 |
Минимальная энергия, необходимая для ионизации атома из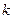 
-го состояния, соответствует переходу электрона с 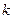-го уровня на уровень и называется энергией ионизации Ei.
Вопросы для самоконтроля
1 Запишите обобщенную формулу Бальмера.
2 Что называется спектральной серией, головной линией и границей спектральной серии?
3 Сформулируйте постулаты Бора.
4 Изложите сущность теории Бора для водородоподобных систем.
5 Изобразите и поясните схему энергетических уровней атома водорода.
6 В чем состоит явление изотопического сдвига?
Задачи
1Основываясь на модели атома, предложенной Бором, получите формулы для расчета радиуса 
-й орбиты и скорости движения электрона в водородоподобном атоме в этом состоянии. Вычислите радиусы первой и второй боровских орбит для электрона, движущегося в атоме водорода и ионах 
, 
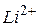. Сравните результаты.
2Определите частоту вращения электрона по второй боровской орбите атома водорода.
3Вычислите для атомарного водорода длины волн головных линий: а) серии Лаймана; б) серии Бальмера; в) серии Пашена.
4Вычислите для однократно ионизированного атома гелия коротковолновые границы (нм): а) серии Бальмера; б) серии Пашена; в) серии Брэкета.
5Определите: а) потенциал ионизации атома водорода; б) первый потенциал возбуждения атома водорода; в) энергию ионизации атома водорода из первого возбужденного состояния.
6Какой серии принадлежит спектральная линия атомарного водорода, волновое число которой равно разности волновых чисел следующих двух линий: 486,1 нм; 410,2 нм? Какова длина волны этой линии?
7Предполагая, что в опыте Франка и Герца вакуумная трубка наполнена не парами ртути, а разреженным атомарным водородом, определите, через какие интервалы ускоряющего потенциала возникнут максимумы на графике зависимости анодного тока от ускоряющего потенциала.
8Вычислите минимальную разрешающую способность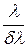 
спектрального прибора, при которой в спектре атомарного водорода можно разрешить первые 20 линий серии Бальмера.
9Вычислите отношение массы протона к массе электрона, если известно, что отношение постоянных Ридберга для тяжелого и легкого водорода 
, а отношение масс ядер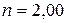 
.
10Определите кинетическую, потенциальную и полную энергию электрона, движущегося по первой боровской орбите: а) в атоме водорода; б) в ионе ; в) в ионе 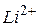. Сравните результаты.
11Определите в электрон-вольтах (эВ) наибольшую и наименьшую энергии фотонов, которые излучаются при совершении атомами водорода переходов, соответствующих серии Лаймана.
12Атомарный водород, возбужденный электромагнитным излучением определенной длины волны, при переходе в основное состояние испускает только три спектральные линии. Определите длины волн этих линий и укажите, каким сериям они принадлежат.
13Атом водорода в основном состоянии поглотил квант света с длиной волны 121,5 нм. Определите радиус электронной орбиты возбужденного атома водорода.
14У какого водородоподобного иона разность длин волн головных линий серии Бальмера и Лаймана равна 59,3 нм?
15Атом водорода, двигавшийся со скоростью 3,26 Мм/с, испустил фотон, соответствующий переходу из первого возбужденного состояния в основное. Найдите угол между направлением вылета фотона и первоначальным направлением движения атома, если кинетическая энергия атома осталась прежней.
16Определите изменение орбитального механического момента электрона, если он переходит из возбужденного состояния в основное с испусканием фотона с длиной волны λ =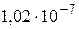 
м.
17В излучении звезды обнаружен водородоподобный спектр, длины волн которого в 9 раз меньше, чем у атомарного водорода. Определите элемент, которому соответствует данный спектр.
18Вычислите энергию фотона, испускаемого при переходе электрона в атоме водорода с третьего энергетического уровня на первый.
19Определите частоту света, излучаемого возбужденным атомом водорода при переходе электрона на второй энергетический уровень, если радиус орбиты электрона изменился в 9 раз.
20Определите, на сколько электрон-вольт изменяется кинетическая энергия электрона в атоме водорода при излучении атомом фотона с длиной волны 486 нм.
21Позитроний – атомоподобная система, состоящая из позитрона и электрона, вращающихся относительно их общего центра масс. Применяя теорию Бора, определите минимальные размеры такой системы.