Экономическая интерпретация на основе производственной задачи.
Рассмотренная симметричная пара взаимно двойственных задач может быть экономически интерпретирована, например, так.
Прямая задача:сколько и какой продукции 
надо произвести, чтобы при заданных стоимостях единицы продукции 
, объемах имеющихся ресурсов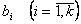 
и нормах расходов 
максимизировать выпуск продукции в стоимостном выражении.
Двойственная задача:какова должна быть оценка единицы каждого из ресурсов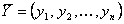 
, чтобы при заданных 
, 
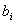и минимизировать общую оценку затрат на всю продукцию.
1.Оптимальное распределение ресурсов.
Допустим для производства продукции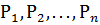 
используются некоторые ресурсы (сырье, оборудование, финансы, рабочая сила) 
в количествах 
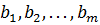. Стоимость единицы ресурса равна 
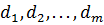тенге. Производство продукции 
ограничено спросом, который оценивается в количестве 
штук 
. Единица продукции 
может быть продана по цене 
и для ее производства необходимо 
единиц ресурса 
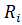(i=1,2,…,m).
Необходимо решить следующую задачу: какое количество продукции необходимо выпустить, чтобы получить максимальную прибыль при ее реализации?
| Виды продукции | Ресурсы | Стоимость | Спрос | |||
| 
| … | 
| |||
| 
| 
| … | 
| 
| 
|
| 
| 
| … | 
| 
| 
|
| … | … | … | ... | … | … | … |
| 
| 
| … | 
| 
| 
|
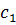
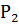
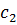
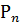
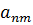
| Количество ресурса | 
| 
| … | 
| ||
| Стоимость ресурса | 
| 
| … | 
|
Обозначим через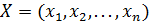 
количество единиц выпускаемой продукции. Не следует выпускать продукции больше, чем диктуется спросом, т.е.
. (1.1)
Количество ресурса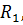 
израсходованного на производство всех рассматриваемых видов продукции 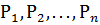, будет равно:
.
Учитывая, что количество ресурса равно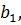 
получим ограничение, определяющее расход ресурса:
.
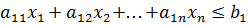Аналогично записываются ограничения, определяющие фактический расход любого из ресурсов 
, т.е.
(1.2)
Очевидно, что количество единиц производимой продукции не может быть отрицательным числом, следовательно:
(1.3)
Прибыль 
, получаемая от реализации продукции, определяется разностью между ценой произведенной продукции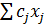 
и ее себестоимостью 
, т.е.
. (1.4)
В итоге получаем математическую форму записи задачи о распределении ресурсов: определить количество выпускаемой продукции 
, которое удовлетворяет линейным неравенствам (1.1)-(1.3) и обеспечивает максимум прибыли – линейной целевой функции (1.4).
2.Загрузка оборудования.
Производство располагает станками трех типов в количествах N1, N2, N3 штук соответственно. Станки могут производить шесть видов продукции: Р1, Р2, Р3, Р4, Р5, Р6. Единица продукции Рj приносит производителю доход cj (j=1,2,…,6). В соответствии с планом должно выпускаться не менее bj (j=1,2,…,6) единиц продукции Рj в месяц. Каждый тип станка может производить любой из перечисленных видов продукции, но в разных количествах. Станок i-го типа (i=1,2,3) может изготавливать единиц готовой продукции (j=1,2,…,6) в месяц. Вопрос: на каких станках производить продукцию, чтобы месячный план был выполнен и стоимость изготовленной продукции была максимальна?
Математическая модель задачи будет иметь вид:
Полная стоимость изготовленной продукции равна
(2.1)
Система ограничений по количеству станков
(2.2)
Согласно имеющемуся плану задание по производству продукции может быть выполнено или перевыполнено. Поэтому соответствующая система ограничений записывается следующим образом:
(2.3)
Неотрицательность количества произведенной продукции выражается неравенством
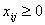. (2.4)
Таким образом, проблема оптимальной загрузки оборудования формулируется следующим образом: определить план производства, который удовлетворяет системам ограничений (2.2)-(2.4) и обеспечивает максимум прибыли – линейной целевой функции (2.1).
3.Оптимальный объем производства.
Фирма выпускает изделия 
четырех видов, для производства которых используются пять технологических операций 
. Рассчитано, что ожидаемая прибыль от продажи изделия равна 
. Эти технологические операции могут также использоваться для других целей. Поэтому время, в течении которого операции 
могут производиться для изготовления рассматриваемых изделий, ограниченно длительностью рабочего дня и равно 
. Длительность технологической операции при изготовлении одного изделия равна . Вопрос: каким должен быть суточный объем производства изделий , чтобы прибыль от их реализации была максимальной?
Условия задачи запишем в таблицу:
| Операции | Изделия | Время использования | |||
|
|
| 
| 
| ||
|
|
| 
| 
|
|
|
|
| 
| 
|
|
| 
| 
| 
| 
| 
|
| 
| 
| 
| 
| 
|
| 
| 
| 
| 
| 
|
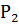
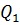
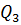
| Стоимость изделия |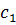
|
| 
| 
|
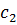
Запишем математическую модель этой задачи. В качестве управляемых переменных можно выбрать количество 
изготовляемых изделий 
. Тогда прибыль от продажи изделий имеет вид:
.
Ограничения, связанные с возможной продолжительностью операций 
, выражаются системой неравенств
Система ограничений должна быть дополнена естественными ограничениями
которые означают, что количество изготовленных изделий каждого вида не может быть отрицательным.
4.Формирование торговой сети.
В регионе расположены населенные пункты, численность жителей которых известна, а также расстояние и стоимость поездок между ними. Кроме того задано множество типовых проектов предприятий общественного питания. Необходимо найти оптимальный план размещения предприятий общественного питания в регионе, обеспечивающий минимальные приведенные затраты на их строительство, эксплуатацию и на поездки жителей между населенными пунктами.
В качестве критерия оптимальности принимаем приведенные затраты С на строительство, эксплуатацию и поездки населения. Тогда формальная запись задачи представляет следующий вид:
Найти такие типовые варианты q предприятий общественного питания для i-го пункта 
и 
численность населения j-го пункта, обслуживаемого предприятиями i-го пункта, которые обеспечивают минимум затрат в соответствии с целевой функцией вида
при следующих условиях-ограничениях
- предложение продукции общественного питания, предоставляемое населению района предприятиями общественного питания i-го пункта, должно соответствовать мощности предприятия:
;
- потребности населения j-го пункта в продукции, обеспечиваемой предприятиями района, должна быть удовлетворена:
;
- расстояние от j-го пункта населения до i-го пункта размещения предприятия не должно превышать допустимого радиуса обслуживания
;
- кроме того, существуют ограничения на переменные .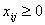
1.Постановка транспортной ЗЛП и ее математическая модель.
Транспортными задачами называются задачи определения оптимального плана перевозок груза из данных пунктов отправления в заданные пункты потребления. Постановка транспортной задачи, которая получила название задачи по критерию стоимости, следующая: в n пунктах отправления Ai находятся соответственно а1,…,аnединиц однородного груза, который должен быть доставлен m потребителям Bj в количестве в1,…, вm единиц. Заданы стоимости cij перевозок единицы груза из i-го пункта отправления к j-му пункту потребления.
Требуется спланировать перевозки так, чтобы максимально удовлетворить потребности и чтобы суммарные затраты на перевозки всего груза были минимальные.
Различают закрытую 
и открытую 
модели транспортной задачи.
Имеются m пунктов отправления 
на которых сосредоточено определенное количество однородного продукта 
. Имеются n пунктов потребления 
, в которые необходимо перевезти следующее количество продуктов 
. Если общая сумма продукта в пунктах отправления равна общей потребности в нем всех пунктов потребления
,
то такая модель называется закрытой, а если не равна, то модель называется открытой. При решении задачи открытая модель приводится к закрытой путем введения фиктивного пункта отправления и потребления.
Из каждого пункта отправления возможна транспортировка продукта в любой пункт потребления, причем стоимость перевозок единицы груза из i-го пункта отправления в j-й пункт потребления 
известна.
Требуется составить такой план перевозок, при котором общие транспортные расходы были бы минимальными. При этом весь продукт из пунктов отправления должен быть вывезен, а потребности каждого потребителя удовлетворены полностью.
За неизвестные здесь принимаются перевозимые объемы груза 
.
Математическая модель транспортной задачи в структурном виде:
при условиях
Транспортная задача также состоит из трех частей: цель задачи, ограничения и условия неотрицательности.
Занесем данные транспортной задачи в специальную таблицу называемуюраспределительной.
 Потребители
Поставщики
| В1 | В2 | … | Вn | Запасы |
| А1 | с11 х11 | с12 х12 | … | с1n х1n | а1 |
| А2 | а2 | ||||
| … | … | … | … | … | … |
| Аm | сm1 хm1 | cm2 хm2 | … | сmn Хmn | аm |
| Потребности | в1 | в2 | … | вn | 
|
2.Метод дифференциальных рент решения транспортной ЗЛП.
Алгоритм метода дифференциальных рент.
1) Заполняется первая распределительная таблица, которая дополняется столбцом для указания избытка и недостатка по строкам и строкой для записи разностей.
2) В каждом из столбцов находится минимальный тариф и обводится кружком.
3) Заполняются клетки с обведенными тарифами, при этом учитываются запасы и потребности соответствующих пунктов, т.е. записывается минимальное число из запаса и потребности.
4) Определяются избыточные (положительные) и недостаточные (отрицательные) строки.
Избыточными считаются строки, в которых остался нераспределенный запас.Если запаса нет, а потребность пункта не удовлетворена, то это недостаточная строка.
Замечание: общая величина избытка совпадает с общей величиной недостатка.
Если остаток в строке равен 0, то в этом случае строка считается положительной при условии, что вторая заполненная клетка, стоящая в столбце, связанном с данной строкой еще одной заполненной клеткой, расположена в положительной строке.
5) Находятся разности между минимальными тарифами, записанными в избыточных строках, и тарифами, стоящими в заполненных клетках в отрицательных строках. Для заполненных клеток стоящих в положительных строках разности не находятся.
6) Выбирается наименьшая из найденных разностей, которая называется промежуточной рентой.
7) Осуществляется переход к новой таблице: тарифы, стоящие в положительных строках переписываются без изменений, а к тарифам стоящим в отрицательных строках прибавляется рента. Затем возврат к пункту 2.
Решение задачи продолжается до тех пор, пока не будут исчерпаны все запасы, и не удовлетворены все потребители.
Замечание: оптимальный план перевозок находим из последней таблицы, а стоимости перевозок берем из первой.
3.Открытая модель транспортной задачи.
Теорема. Для разрешимости транспортной задачи необходимо и достаточно, чтобы запасы груза в пунктах отправления были равны потребностям в грузе в пунктах потребления.
.
В случае превышения запаса над потребностью вводится фиктивный (n+1) пункт назначения с потребностью 
и при этом транспортные расходы равны нулю 
.
Если потребности больше, чем запасы, то вводится фиктивный (m+1) пункт отправления с запасом груза 
, здесь также транспортные расходы равны нулю 
.