Лабораторная работа № 1. Изучение динамики систем автоматического регулирования дуговой сварки методом математического моделирования

 

1.1. Общие сведения

 

Кривую переходного процесса (переходную характеристику) X_вых=f(t) можно построить, решив общее дифференциальное уравнение системы автоматического регулирования (САР).

C помощью математического моделирования можно довольно просто решать дифференциальные уравнения высоких порядков, описывающие работу САР. При математическом моделировании используется подобие дифференциальных уравнений, которые описывают процессы, происходящие в реальном элементе и в модели. Моделирование обычно осуществляется с помощью вычислительных машин непрерывного действия. Такие машины построены на основе операционных усилителей (рис. 1.1).

 

 

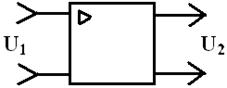
Рис. 1.1. Операционный усилитель

 

Реальные конструкции их сложны. Мы будем считать, что усилитель – это четырехполюсник, для которого

 

U₂ = – K U₁ , (1.1)

 

где K – коэффициент усиления, имеющий большую величину (10⁴÷10⁵).

Кроме этого сопротивление между выходными зажимами равно бесконечности, а, следовательно, ток во входной цепи равен нулю. Знак минус является следствием особенностей конструкции усилителя (нечетность каскадов усиления).

Для выполнения математических операций к усилителю подключаются два сопротивления (рис. 1.2,а): входное Z_вх и обратной связи Z_ос. В зависимости от вида сопротивлений (активное или индуктивное) операционный усилитель может выполнять операции, необходимые при решении дифференциальных уравнений, а именно – интегрирования, суммирования и умножения на постоянный коэффициент.

Рассмотрим три варианта.

 

1) Z_вх и Z_ос – активные сопротивления R_вх и R_ос (рис. 1.2,б).

 

Из определения усилителя мы знаем, что ток в точке О должен быть равен нулю. Поэтому:

; ; .

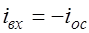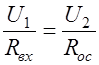Следовательно, при активных сопротивлениях операторный блок выполняет функцию умножения на постоянный коэффициент 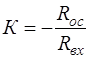. При R_вх = R_ос такой блок выполняет функцию перемены знака U₂ = – U₁. Обычно принимают R_ос = 1, поэтому .

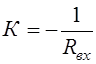2) Пусть на входах 1, 2, ..., n блока, показанного на рис. 1.2,г, относительно общей нулевой точки приложены напряжения

U_о1, U_о2, U_о3, ..., U_оn, а на выходе действует напряжение U.

Для токов, текущих через сопротивления, получаем непосредственно:

 

; ; ; .

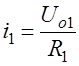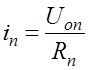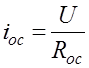Из условия равенства нулю суммы токов, протекающих в точке О, получим:

;

. (1.2)

 

 

 

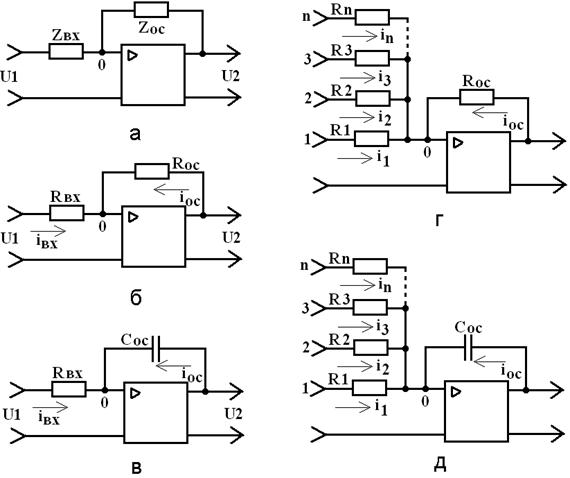
Рис. 1.2. Варианты включения операционных усилителей

 

Таким образом, данный блок выполняет функцию перемены знака и суммирования входных напряжений, каждое из которых умножено на постоянный коэффициент, величина которого зависит от соотношения R_ос и R_i. Такой блок называется сумматором.

 

3) Z_вх – активное сопротивление R_вх; Z_ос – емкостное сопротивление. При емкости конденсатора С_ос имеем:

; ; ; ;

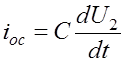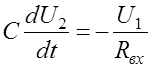. (1.3)

где U_o – значение переменной при t = 0 (начальное условие).

Таким образом, блок, показанный на рис. 1.2,в, выполняет операцию интегрирования и перемены знака. Если на вход данного блока подается несколько напряжений через входные сопротивления R₁, R₂, ..., R_n (рис. 1.2,д), то данный блок будет выполнять операцию интегрирования суммы, т.е. совмещать функции блоков суммирования и интегрирования в одном блоке.

Обычно в аналоговых машинах величина С_ос (как и R_ос) принимается равной «1».

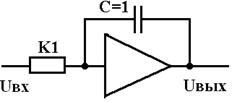
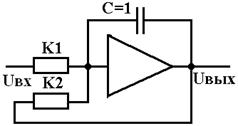
С помощью рассмотренных выше блоков можно моделировать типовые динамические звенья. Например, схему, показанную на рис. 1.2,б, можно рассматривать как модель усилительного звена с передаточной функцией W(p)= – К, где , а схему на рис. 1.2,в – как модель интегрирующего звена с передаточной функцией , где 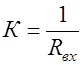. Аналогично можно представить и модели других звеньев (табл. 1.1).

В табл. 1.1 операционные усилители изображены условно в виде треугольников. В дальнейшем будем пользоваться таким обозначением.

Таким образом, любую структурную схему САР, состоящую из типовых динамических звеньев, можно представить моделью, заменив типовые звенья их моделями согласно табл. 1.1.

 

Таблица 1.1

Математические модели различных звеньев

 

№ п/п	Машинная схема	Передаточная функция	Коэффициенты модели
		W(p) = – 1	K1 = 1
		W(p) = – K	K1 = K
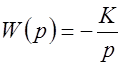
			K1 = K

 

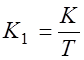
В качестве примера составим упрощенную модель системы АРДС. Для этого составим вначале упрощенную структурную схему системы «источник питания - автомат - дуга (без сварного шва)».

Рассмотрим случай автоматической сварки под слоем флюса тонкой проволокой на автомате с постоянной скоростью подачи (АБС, ТС-17 и др.).

Для этого случая процесс плавления электрода можно считать безинерционным, а статическую характеристику дуги жесткой. Кроме этого не будем учитывать колебания длины дуги вследствие переноса металла и изменения вылета. Источником питания является выпрямитель с индуктивностью в цепи выпрямления тока.

При сделанных допущениях система саморегулирования описывается следующими уравнениями:

1) Считая процесс плавления электрода безинерционным, можем записать:

V_o = К_ст I_д - К_сн U_д (1.4)

или в отклонениях:

DV_э(p) = DV_эi + DV_эu = W₁(p) DI(p) + W₂(p) DU(p) , (1.5)

 

где: V_э – скорость плавления электрода;

К_ст – коэффициент саморегулирования по току;

К_сн – коэффициент саморегулирования по напряжению.

 

2) Изменение скорости плавления электрода (DV_э) вызывает при постоянной скорости подачи изменение длины дуги (Dl):

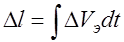(1.6)

или в операторной форме:

, (1.7)

где .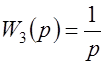

 

3) Известна зависимость между изменением длины дуги и напряжением:

DU = β Dl (1.8)

или в операторной форме:

DU(p) = W₄(p) Dl(p) , (1.9)

 

где W₄(p) = β – градиент напряжения в столбе дуги.

 

4) Напряжение и ток связаны между собой зависимостью U_д=f(I), которая зависит от свойств источника питания и в общем случае не является линейной. Кроме этого, источник питания вследствие наличия индуктивности L является инерционным звеном, которое после линеаризации внешней характеристики источника питания описывается дифференциальным уравнением:

, (1.10)

где 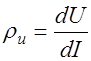– динамическое сопротивление источника питания;

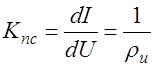– коэффициент питающей системы.

В операторной форме уравнение (1.10) имеет вид:

(1.11)

или

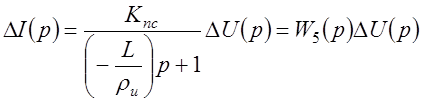, (1.12)

где .

 

Составленная по формулам (1.5), (1.7), (1.9) и (1.12) структурная схема системы АРДС показана на рис. 1.3.

Данную схему можно заменить математической моделью, заменив типовые звенья их моделями согласно табл.1 и соединив их, как показано на рис. 1.3.

Полученная таким образом машинная схема системы АРДС показана на рис. 1.4.

Теперь, задаваясь типом входного воздействия ( 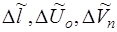и т.д.), можно на индикаторе получить кривую переходного процесса любого параметра структурной схемы.

 

 

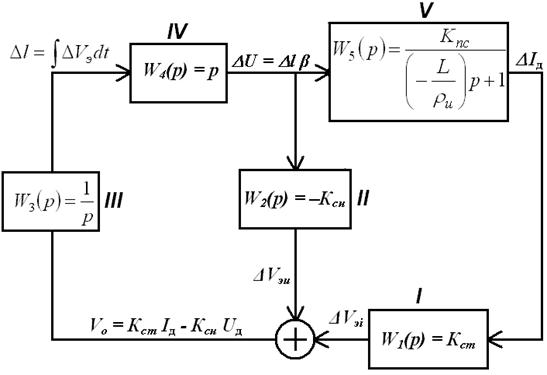
Рис. 1.3. Структурная схема системы АРДС

 

 

 

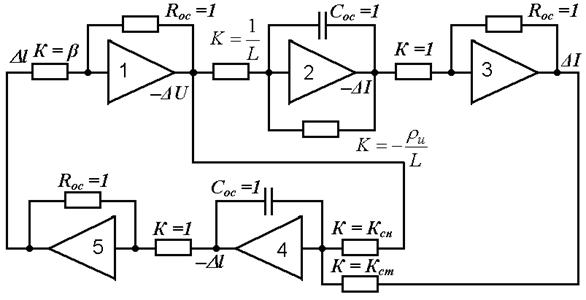
Рис. 1.4. Машинная схема системы АРДС

 

 

В данной работе студенты изучают влияние параметров САР (L, r_и, К_ст, b – по указанию преподавателя) на характер переходного процесса DI(t) и DU(t) в системе АРДС при возмущении по длине дуги Dl. Возмущение 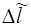вызывает, как и сигнал Dl, согласно уравнению (1.8), изменение напряжения DU, поэтому его необходимо подавать на вход усилителя 1 через дополнительное входное сопротивление с К=b.

 

1.2. Цель работы

 

Изучить динамику работы систем автоматического регулирования процессов дуговой сварки с помощью математического моделирования на ЭВМ на примере системы саморегулирования (АРДС).

 

1.3. Порядок выполнения работы

 

1.3.1. Изучить раздел «Общие сведения».

1.3.2. Составить машинную схему системы АРДС при ступенчатом возмущении по длине дуги.

Примечание: Значения постоянных коэффициентов, входящих в передаточные функции W₁(p)...W₅(p), задаются преподавателем.

1.3.3. Собрать машинную схему на наборном поле аналоговой машины МН-7. (Порядок работы на МН-7 см. в ПРИЛОЖЕНИИ).

1.3.4. Зарисовать в масштабе переходные процессы по току и напряжению, наблюдаемые на экране осциллографа при ступенчатом изменении длины дуги и изменении (по указанию преподавателя) одного из параметров САР.

1.3.5. Сделать вывод о характере регулирования в системе АРДС при возмущении по длине дуги (статическое, астатическое) и о влиянии параметров АР на характер переходного процесса.

 

1.4. Содержание отчета

 

· Цель и задачи работы.

· Машинная схема.

· Рисунки осциллограмм переходных процессов.

· Выводы.

 

1.5. Контрольные вопросы

 

· Почему для анализа переходных процессов в САР используется математическое моделирование?

· Какие математические действия можно выполнять с помощью операционного усилителя?

· Что необходимо сделать, чтобы операционный усилитель выполнял ту или иную математическую операцию?

· Что необходимо иметь для составления машинной схемы САР?

· На основании чего строится структурная схема САР?

· Какая система называется системой АРДС?

· Какие условия необходимы для работы системы АРДС?

· Как проводится анализ переходных процессов в САР с помощью машинной схемы?

 

Лабораторная работа №2. Исследование влияния типа системы автоматического регулирования дуговой сварки на характер переходного процесса при возмущении по длине дуги с помощью аналоговой вычислительной машины

 

2.1. Общие сведения

 

В предыдущей работе с помощью математического моделирования исследовался переходной процесс в системе саморегулирования (АРДС). В отличие от системы саморегулирования (АРДС) в системах автоматического регулирования напряжения (АРНД) и автоматического регулирования тока (АРТД) поддержание постоянства энергетических параметров осуществляется с помощью специальных регуляторов напря­жения (в системе АРНД) и тока (в системе АРТД). Однако явление саморегулирования здесь также присутствует, поэтому системы АРНД и АРТД будут описываться теми же уравнениями, что и АРДС плюс уравнение работы регуляторов.

 

2.1.1. Система автоматического регулирования напряжения (АРНД)

 

Принципиальная схема системы АРНД с воздействием на скорость подачи электрода (V_п) показана на рис. 2.1,а.

Напряжение на дуге U_д сравнивается в устройстве СУ с заданным напряжением U_з. Разность напряжений (U_д–U_з) пос­ле усиления подается на якорь приводного двигателя. Таким образом, скорость подачи электрода является функцией напряжения на дуге:

 

V_п = k_рн(U_д – U_з) , (2.1)

где – коэффициент усиления регулятора напряжения.

 

а б

 

Рис. 2.1. Системы автоматического регулирования дуги с

воздействием на скорость подачи электрода:

а – система АРНД; б – система АРТД

 

При случайном увеличении длины дуги напряжение U_д увеличива­ется, скорость подачи согласно уравнения (2.1) возрастает, что приводит к укорочению дуги и восстановлению ее начального значения.

Если пренебречь инерционностью регулятора, которая мала по сравнению с инерционностью тепловых процессов в сварочной ванне, то уравнение (2.1) в отклонениях запишется:

 

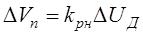. (2.2)

 

Изменение скорости перемещения торца электрода относительно изделия ΔV, вызывающее изменение длины дуги Δl, будет равно разности изменения скоростей плавления ΔV_э и подачи ΔV_п электрода.

ΔV = ΔV_э – ΔV_п = ΔV_э + (– ΔV_п) = ΔV_э + (– k_рн) ΔU_д . (2.3)

 

Таким образом структурная схема системы АРНД (рисунок 2.2) будет отличаться от от структурной схемы саморегулирования (рис. 1.3) наличием звена VI с передаточной функцией W₅(p) = – k_рн, отражающего работу регулятора напряжения.

 

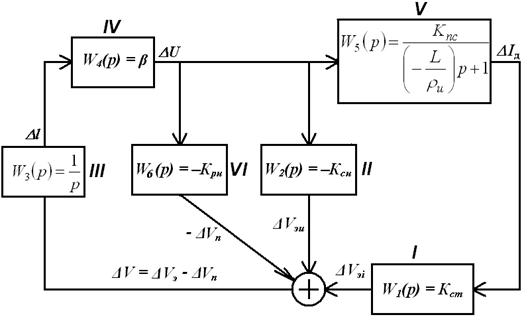
Рис. 2.2. Структурная схема системы АРНД

Звено VI включено параллельно звену II. Если объединить эти звенья, получим одно звено с передаточной функцией равной – (k_сн+k_рн). Поэтому систему АРНД можно pассматривать как систему АРДС с искусственно увеличенным саморегулированием по напряжению. Структурную схему системы АРНД можно получить заменив в структурной схеме APДC (рис. 1.3) k_сн суммой (k_сн+k_рн).

Аналогично для математического моделирования можно воспользоваться машинной схемой системы АРДС (рис. 1.4), заменив коэффициент k_сн суммой (k_сн+k_рн).

 

2.1.2. Система автоматического регулирования тока (АРТД)

 

Принципиальная схема системы АРТД с воздействием на скорость подачи проволоки V_п приведена на рис. 2.1,б. Падение напряжения на сопротивлении R, пропорциональное величине сварочного тока, сравнивается в устройстве СУ с напряжением, характеризующим за­данное значение тока I_з. Разность этих величин после усиления подается на якорь приводного двигателя. Таким образом, скорость подачи электрода является функцией тока:

V_п = k_рт(I_з – I_д) . (2.4)

где 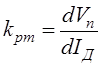– коэффициент усилителя регулятора тока.

При случайном увеличении длины дуги ток I_д уменьшается, скорость подачи согласно уравнению (2.4) возрастает, что приводит к укорочению дуги и восстановлению ее начального значения.

Если пренебречь инерционностью регулятора, которая мала по сравнению с инерционностью тепловых процессов в сварочной ванне, то уравнение (2.4) в отклонениях запишется:

 

ΔV_п = – k_рт ΔI_д . (2.5)

 

Изменение скорости перемещения торца электрода относительно изделия ΔV, вызывавшее изменение длины дуги Δl, будет равно разности изменения скоростей плавления ΔV_э и подачи ΔV_п электрода

ΔV = ΔV_э – ΔV_п = ΔV_э + (– ΔV_п) = ΔV_э + k_рт ΔI_д . (2.6)

 

Таким образом, структурная схема системы APTД (рис. 2.3) будет отличаться от структурной схемы системы саморегулирования (рис. 1.3) наличием эвена УП с передаточной функцией W₇(p) = k_рт, отражающего работу регулятора тока.

Звено VII включено параллельно звену I. Если объединить эти звенья получим одно звено с передаточной функцией равной (k_ст+k_рт). Поэтому систему АРТД можно рассматривать как систему АРДС с искусственно увеличенным саморегулированием по току. Структур­ную схему системы АРТД можно получить заменив в структурной схеме АРДС (рис. 1.3) k_ст суммой (k_ст+k_рт).

Аналогично для математического моделирования можно восполь­зоваться машинной схемой системы АРДС (рис. 1.4) , заменив коэффициент k_ст суммой (k_ст+k_рт).

 

 

Рис. 2.3. Структурная схема системы АРТД

2.2. Цель работы

 

Изучить влияние типа системы автоматического регулирования дуговой сварки на характер переходного процес­са и скорость отработки возмущения по длине дуги.

 

2.3. Порядок выполнения работы

 

2.3.1. Изучить раздел «Общие положения».

2.3.2. Составить машинную схему для моделирования АРНД при сту­пенчатом возмущении по длине дуги (значения постоянных коэффициентов и величина возмущения задаются преподавателем).

2.3.3. Собрать машинную схему на наборном поле машины МН-7 (по­рядок работы на МН-7 см. в ПРИЛОЖЕНИИ).

2.3.4. Зарисовать в масштабе переходные процессы по току и напряжению, наблюдаемые на экране осциллографа при ступенчатом измене­нии длины дуги и изменении наклона внешней характеристики источника литания (ρ_и).

2.3.5. Проделать указанное в пунктах 2.3.2 - 2.3.4 для системы АРТД.

2.3.6. Сравнить с данными, полученными в работе №1 и сделать вывод о влиянии типа системы автоматического регулирования на харак­тер переходного процесса и скорость отработки возмущений.

 

2.4. Содержание отчета

 

· Наименование и цель работы.

· Машинные схемы.

· Зарисовки осциллограмм переходных процессов.

· Выводы.

 

2.5. Контрольные вопросы

 

· Чем отличается система АРНД от системы АРДС?

· Сравнительная оценка систем АРДС и АРНД;

· Принцип работы системы АРТД.

 

Лабораторная работа № 3. Исследование влияния типа САР энергетических параметров дуговой сварки на характер переходного процесса и величину статических ошибок по току и напряжению при возмущении со стороны источника питания

 

3.1. Общие сведения

 

Одним из наиболее часто встречающихся на практике возмущений является возмущение по напряжению холостого хода источника питания 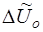. Оно вызывается, как правило, колебаниями напряжения питающейся сети. САР энергетических параметров АРДС, АРНД и АРТД данное возмущение полностью не отрабатывают. После окончания переходного процесса ток и напряжение отличаются от первоначальных значений на величину статической ошибки.

 

3.1.1. Система саморегулирования (АРДС)

 

На рис. 3.1 показана линеаризованная внешняя характеристика источника питания (линия 1) и статическая характеристика системы АРДС (2). В состоянии равновесия режим сварки определяется точкой пересечения внешней характеристики источника питания и статической характеристики системы АРДС (точка А). При ступенчатом изменении напряжения холостого хода 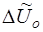внешняя характеристика источника питания сместится, как показано на рис. 3.1 (линия 3).

Если индуктивность равна L = 0, то одновременно с напряжением, также ступенчато, изменится ток на величину DI_o (рис. 3.1), и режим сварки сместится в точку В. Затем, вследствие нарушения равенства скоростей подачи V_п и плавления электрода V_э, начинается процесс саморегулирования, при котором возникает дополнительное отклонение тока DI_p. Это отклонение имеет знак противоположный знаку DI_o. В результате этого режим смещается в новую точку равновесия С, где ток и напряжение будут отличаться от первоначальных значений на величину статических ошибок, соответственно DI_у и DU_у. Таким образом, отклонение тока DI в данном случае будет равно:

DI = DI_о + DI_p , (3.1)

 

где DI_о и DI_p в общем случае (L ≠ 0) определяются по формулам (см. работу №1):

 

Рис. 3.1. Реакция системы АРДС на возмущение по напряжению холостого хода источника питания

 

, (3.2)

 

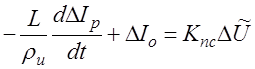. (3.3)

 

В операторной форме:

 

DI_p(p) = W₅(p) DU(p) ; (3.4)

 

DI_o(p) = W₅(p) DU_o(p) , (3.5)

где

.

С учетом выражений (3.4) и (3.5), а также равенства (3.1) структурная схема система АРДС при возмущении по напряжению холостого хода будет иметь вид, показанный на рис. 3.2.

 

 

Рис. 3.2. Структурная схема системы АРДС при возмущении

по напряжению холостого хода источника

 

Поскольку при падающей внешней характеристике источника питания (r_и<0) увеличение напряжения холостого хода 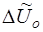вызывает положительное изменение +DI_o и наоборот (рис. 3.1), в структурную схему вводится дополнительное звено VII с передаточной функцией, равной «–1».

Для математического моделирования данной схемы можно воспользоваться машинной схемой системы АРДС (рис. 1.4), дополнив ее машинной схемой звеньев VI и VII.

При составлении машинной схемы звено VII можно исключить, подав на вход , а звено VI заменить машинной схемой (см. табл. 1.1). При этом, так как операционный усилитель меняет знак, то на выходе машинной схемы получим –DI_o. Этот сигнал необходимо подать на вход усилителя 3 (рис. 1.4), где он суммируется с сигналом –DI_р и сумма меняет знак. В результате на выходе усилителя 3 (рис. 1.4) получим величину DI = DI_p + DI_о.

 

3.1.2. Система автоматического регулирования напряжения дуги (АРНД)

 

Систему АРНД можно рассматривать как систему саморегулирования с искусственно увеличенным саморегулированием по напряжению. Для анализа системы АРНД можно воспользоваться машинной схемой саморегулирования, увеличив коэффициент саморегулирования по напряжению К_сн на величину К_рн (коэффициента усиления регулятора напряжения).

 

3.1.3. Система автоматического регулирования тока (АРТД)

 

Систему АРТД можно рассматривать как систему саморегулирования с искусственно увеличенным саморегулированием по току. Для анализа системы АРТД можно воспользоваться машинной схемой системы саморегулирования, увеличив коэффициент саморегулирования по току К_ст на величину К_рт (коэффициент усиления регулятора тока).

 

3.2. Цель работы

 

Изучить, как влияет тип САР (АРДС, АРНД, АРТД) на характер переходного процесса и величину статических ошибок при возмущении по напряжению холостого хода источника питания .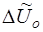

 

3.3. Порядок выполнения работы

 

3.3.1. Изучить раздел «Общие сведения».

3.3.2. Составить машинную схему для моделирования системы АРДС при ступенчатом возмущении по напряжению холостого хода (значения постоянных коэффициентов и величины возмущения задаются преподавателем).

3.3.3. Собрать машинную схему на наборном поле машины МН-7 (Порядок работы на МН-7 см. в ПРИЛОЖЕНИИ).

3.3.4. Зарисовать в масштабе переходные процессы по току и напряжению, наблюдаемые на экране осциллографа при ступенчатом изменении напряжения холостого хода. Определить величину статических ошибок в процентах.

3.3.5. Проделать указанное в пунктах 3.3.2 – 3.3.4 для систем АРНД при заданном значении К_рн.

3.3.6. Проделать выше указанное для системы АРТД при заданном значении К_рт.

3.3.7. Сравнить результаты и сделать вывод о влиянии типа САР на характер переходного процесса, быстродействие и величину статических ошибок по току и напряжению.

 

3.4. Содержание отчета

 

· Цель и задачи работы.

· Машинные схемы.

· Рисунки осциллограмм переходных процессов.

· Выводы.

 

3.5. Контрольные вопросы

· Статическая характеристика системы АРДС;

· Статические свойства системы АРДС;

· Статическая характеристика системы АРНД;

· Статические свойства системы АРНД;

· Статическая характеристика системы АРТД.