Дискретные случайные величины: законы распределения и числовые характеристики.

Случайной величиной называется действительная функция , определённая на пространстве элементарных исходов 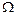и такая, что при всех действительных события принадлежат 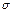-алгебре событий для данного эксперимента. Таким образом, под случайной величиной понимают величину, принимающую свои возможные значения в зависимости от исхода эксперимента, с которым она связана.

Законом распределения (вероятностей) случайной величины называют любое правило, позволяющее найти вероятность того, что случайная величина примет значение из некоторого подмножества своих возможных значений. Общим законом распределения, присущим всем случайным величинам, является функция распределения.

Функцией распределения (вероятностей) случайной величины называется функция действительной переменной , , определяемая формулой .

Каждая функция распределения обладает следующими свойствами:

1) , ; 2) не убывает;

3) , ; 4) непрерывна слева.

Любая неубывающая непрерывная слева действительная функция , удовлетворяющая условиям и , является функцией распределения некоторой случайной величины.

Вероятность события определяется формулой:

.

Случайная величина называется дискретной случайной величиной (ДСВ), если множество её возможных значений конечно или счётно, причём , , где суммирование распространяется на все возможные значения . Функция распределения в этом случае имеет ступенчатый вид и задаётся формулой , где суммирование распространяется на все значения индекса , для которых .

Закон распределения ДСВ удобно задавать рядом распределения. Рядом распределения ДСВ называют таблицу, в которой перечислены все возможные значения этой случайной величины и соответствующие им вероятности . Для наглядности закон распределения ДСВ изображают графически, для чего в прямоугольной системе координат строят точки и соединяют их отрезками прямых. Полученную фигуру называют многоугольником распределения.

Математическим ожиданием дискретной случайной величины называется число , если ряд сходится абсолютно.

Дисперсией случайной величины называется неотрицательное число . Число называется средним квадратичным отклонением.

Дисперсию дискретной случайной величины вычисляют по формулам:

или .

Пусть -постоянная величина. Математическое ожидание и дисперсия случайной величины обладают следующими свойствами:

Свойства математического ожидания: 1) ; 2) ; 3) ; 4) , если и независимы.

Свойства дисперсии: 1) ; 2) ; 3) ; 4) ; 5) , если и независимы.

 

В задачах 12.131-12.136требуется: а) составить закон распределения дискретной случайной величины и построить многоугольник полученного распределения; б) вычислить математическое ожидание и дисперсию .

12.131Устройство состоит из трёх независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте равна 0.1. Случайная величина - число отказавших элементов в одном опыте.

12.132В партии из 10 деталей имеется 8 стандартных. Наудачу отобраны две детали. Случайная величина - число стандартных деталей среди отобранных.

12.133В урне 6 белых и 4 чёрных шара. Из неё три раза подряд извлекают шар, причём каждый раз вынутый шар возвращают в урну и шары перемешивают. Случайная величина - число извлечённых белых шаров.

12.134Два стрелка независимо друг от друга делают по одному выстрелу в мишень. Вероятность попадания в мишень для первого стрелка – 0.8, для второго – 0.9. Случайная величина - суммарное число попаданий в мишень.

12.135Стрелок ведёт стрельбу по цели с вероятностью попадания при каждом выстреле 0.8. За каждое попадание он получает 5 очков, а в случае промаха очков ему не начисляют. Произведено три выстрела. Случайная величина - число очков, полученных стрелком.

12.136Рабочий обслуживает три станка. Вероятность того, что станок в течение времени потребует внимания рабочего, для первого станка равна 0.1, для второго – 0.2, для третьего – 0.3. Случайная величина - число станков, не требующих внимания рабочего в течение времени .

12.137Дискретная случайная величина задана рядом распределения . Найти значение её функции распределения

12.138Известны математические ожидания и дисперсии независимых случайных величин и : , , , . Найти математическое ожидание и дисперсию случайной величины , если: а) ; б) .

12.139Дискретная случайная величина принимает три возможных значения: с вероятностью ; с вероятностью и с вероятностью . Найти и , зная, что .

12.140Дан перечень возможных значений дискретной случайной величины : , , , а также известны математические ожидания этой величины и её квадрата: , . Найти закон распределения величины .

12.141Дискретная случайная величина Х имеет только два возможных значения: ( ). Вероятность, что Х примет значение , равна 0.2. Найти закон распределения Х, зная, её математическое ожидание и среднее квадратичное отклонение

12.142Дискретная случайная величина Х имеет только три возможных значения: причем Вероятности того, что Х примет значения соответственно равны 0.3 и 0.2. Найти закон распределения величины Х, зная ее математическое ожидание и дисперсию .

12.143Вероятность сдать экзамен по «Теории вероятностей» студентом на «5» равна 0.3; на «4» - 0.4. Найти вероятности получения оценок «2» и «3», если известно, что средний балл, получаемый студентами на экзамене .

12.144 Известны математические ожидания и дисперсии независимых случайных величин и : , , , . Найти математическое ожидание случайной величины , если:

а) ; б) .

12.145Распределение дискретной случайной величины определяется формулами: , . Требуется найти:

а) неизвестную постоянную 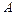; б) .