Косозубые и шевронные цилиндрические передачи
Расчет основных размеров проводят по формулам п. 1.3.6.1, за исключением диаметров d1 и d2 . Принимают:
Далее размеры da1 , da2 , df1 и df2 вычисляют в функции делительных диаметров d1 и d2.
Коэффициент торцового перекрытия для косозубых передач:
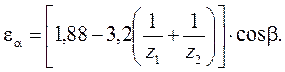
Коэффициент осевого перекрытия:
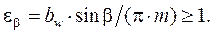
Суммарный коэффициент перекрытия:
e = ea + eb.
1.3.8. Геометрический расчет ортогональной эвольвентной
зубчатой передачи коническими колесами
В редукторе по схеме 23 (рис. 1.5) быстроходная передача коническая, геометрический расчет которой имеет существенные особенности.
Задание на расчет оформляется в виде таблице по форме, приведенной в табл. 1.1.
В столбце код схемы редуктора указывают 23, в столбце код передачи для быстроходной указывают цифру 4, а в столбце для тихоходной цифры 1, 2 или 3 в соответствии с заданием и разделом 1.2.1.6.
Параметры yba Т и yba Б выбираются в соответствии с п. 1.2.1.4.
Остальные параметры записывают также, как описано в разделе 1.2.
Распечатка содержит геометрические и кинематические параметры, объединенные в несколько идентичных групп. Идентификаторы, содержащиеся в распечатке, аналогичны приведенным в разделе 1.3.1 со следующими особенностями:
B – ширина венца зубчатых колес;
U – передаточное число конической передачи, u = z2 / z1. Заметим, что u > 3,5 нежелательно, поскольку габариты колеса конической передачи могут оказаться неприемлемо большими – возможно задевание этого колеса поверхности тихоходного вала;
MOD – внешний окружной модуль mte;
D1, D2 – соответственно, внешние делительные диаметры шестерни и колеса, de1 и de2;
BETA – угол наклона зубьев цилиндрического косозубой передачи, b°.
1.3.8.1. Последовательность геометрического расчета
Исходный контур соответствует ГОСТ 13754-81 и определяет:
– a – угол профиля, принято a = 20°;
– 
– коэффициент высоты головки (ножки) зуба, 
;
– 
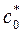– коэффициент радиального зазора, 
.
Коэффициенты смещения для конических передач обеспечивают: влияние на угол зацепления aw (при этом, углы начальных конусов шестерни и колеса не меняются, а углы делительных конусов не совпадают с ними и меняют значения); возможность выравнивания толщины зубьев шестерни и колеса, например, для повышения изгибной прочности зубьев шестерни.
Во втором варианте принимают:
– суммарный коэффициент смещения XS = 0;
– коэффициенты изменения расчетной толщины зуба, Xt.
Обычно Xt1 + Xt2 = XS = 0, т.е. коэффициенты Xt1 и Xt2 равны по модулю и противоположны по знаку.
Рекомендуется определять Xt по эмпирической формуле
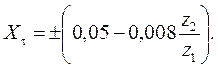
Поскольку окружные шаги шестерни и колеса измеренные на любом участке зуба по его длине неодинаковы, значения модуля зацепления тоже неодинаково. Поэтому, возможно применение передач с нестандартными модулями на дополнительном (внешнем) конусе. Однако, с целью унификации средств измерения и контроля, рекомендуется выбирать модуль в соответствии с ГОСТ 9563-60.
Основные размеры конической шестерни (индекс 1) представлены на рис. 1.7. Отметим, что аналогичные размеры для колеса отмечаются индексом 2 и показаны на рис. 1.8.
Углы делительных конусов для ортогональной конической передачи d1 и d2 определяются условиями
d1 + d2 = å = 90°.
В общем случае, при произвольном значении межосевого угла
å ≠ 90°
Размеры dк и l определяются в процессе дальнейшего проектирования (рис. 1.8). Необходимо руководствоваться соотношением
l ≥ (1…1,2)∙dк.
d2 = å – d1.
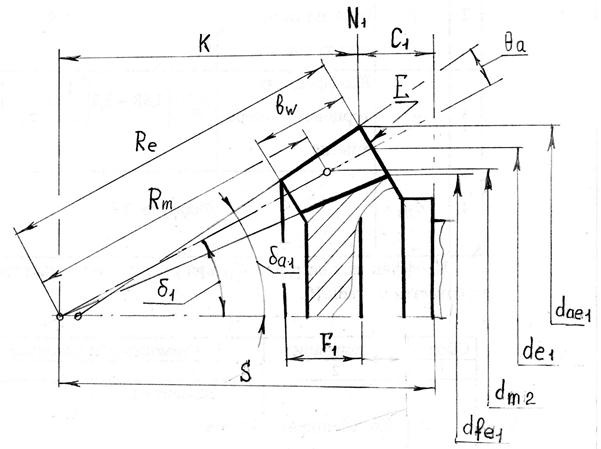
Рис. 1.7
Рис. 1.8
Отметим, что передаточное число ортогональной передачи может быть найдено из соотношения
u = tg d2 = z2 / z1.
Далее, в соответствии с рис. 1.7, 1.8.
Внешние делительные диаметры колес (могут быть заимствованы из распечатки):
de1 = mte ∙ z1;
de2 = mte ∙ z2.
Внешнее делительное конусное расстояние
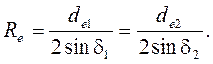
Ширина зубчатого венца
bw = Kbe ∙ Re.
Значение Kbe не должно превышать значения 0,285, а для ширины зубчатого венца рекомендуется bw ≤ 10∙mte.
Среднее делительное конусное расстояние
Rm = Re – 0,5∙bw.
Средний модуль зацепления
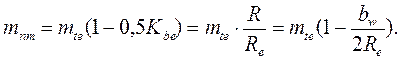
Средние делительные диаметры
dm1 = mnm ∙ z1,
dm2 = mnm ∙ z2 = dm1 ∙ u.
Расстояние от плоскостей N1 или N2 до задней плоскости зубчатого колеса передачи C, приближенно, для шестерни и колеса, соответственно
C1 » 4∙mte∙sind1; C2 » 4∙mte∙sind2.
Для шестерни размер C1 определяется конструкцией узла быстроходного вала редуктора и вышеприведенная рекомендация не всегда актуальна.
Углы конуса вершин для шестерни и колеса
da1 = d1 + qf2,
da2 = d2 + qf1.
В этих формулах qf1 и qf2 определяются по формулам
Приведенные формулы справедливы для осевой формы зубьев 1, характерной для прямозубых конических колес.
Конструктивные параметры F1 и F2 находим из соотношений:
F1 » bw∙cosda2; F2 » b2∙cosda1.
Размер C1 определяется компоновкой с учетом того положения шестерни относительно подшипников быстроходного вала и корпуса редуктора и не может быть однозначно принятым.
Диаметры окружностей вершин на дополнительных конусах подсчитывают по формулам (см. рис. 1.7 и 1.8)
,
.
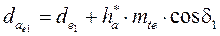Диаметры окружностей впадин
,
.
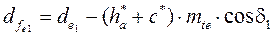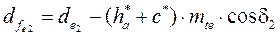На рис. 1.5 показано расположение колеса и шестерни конической передачи редуктора по схеме 23. Заметим, что желательно симметричное по отношению к корпусу положение оси быстроходного вала, при этом размер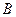 
должен соответствовать выражению
B = 2 (С2 + F2 + a) » 2 (bw(Т) + 2a).