Кинетическая и полная энергия в теории относительности

Кинетиìческая энеìргия — скалярная функция, являющаяся мерой движения материальной точки и зависящая только от массы и модуля скорости материальных точек, образующих рассматриваемую физическую систему, энергия механической системы, зависящая от скоростей движения её точек в выбранной системе отсчёта. Часто выделяют кинетическую энергию поступательного и вращательного движения.

Более строго, кинетическая энергия есть разность между полной энергией системы и её энергией покоя; таким образом, кинетическая энергия — часть полной энергии, обусловленная движением

Простым языком, кинетическая энергия - это энергия, которую тело имеет только при движении. Когда тело не движется, кинетическая энергия равна нулю.

Рассмотрим систему, состоящую из одной частицы, и запишем второй закон Ньютона:

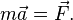
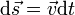— есть равнодействующая всех сил, действующих на тело. Скалярно умножим уравнение на перемещение частицы . Учитывая, что получим:

Если система замкнута, то есть внешние по отношению к системе силы отсутствуют, или равнодействующая всех сил равна нулю, то

а величина где - масса тела; - скорость центра масс тела;

- момент инерции тела; - угловая скорость тела.

Свойства кинетической энергии:

Аддитивность. Это свойство означает, что кинетическая энергия механической системы, состоящей из материальных точек, равна сумме кинетических энергий всех материальных точек, входящих в систему.

Инвариантность по отношению к повороту системы отсчета. Кинетическая энергия не зависит от положения точки, направления её скорости и зависит лишь от модуля скорости или, что то же самое, от квадрата её скорости.

 

Сохранение. Кинетическая энергия не изменяется при взаимодействиях, изменяющих лишь механические характеристики системы.Это свойство инвариантно по отношению к преобразованиям Галилея .Свойства сохранения кинетической энергии и второго закона Ньютона достаточно, чтобы вывести математичекую формулу кинетической энергии.

Соотношение кинетической и внутренней энергии:

Кинетическая энергия зависит от того, с каких позиций рассматривается система. Если рассматривать макроскопический объект (например, твёрдое тело видимых размеров) как единое целое, можно говорить о такой форме энергии, как внутренняя энергия. Кинетическая энергия в этом случае появляется лишь тогда, когда тело движется как целое.

То же тело, рассматриваемое с микроскопической точки зрения, состоит из атомов и молекул, и внутренняя энергия обусловлена движением атомов и молекул и рассматривается как следствие теплового движения этих частиц, а абсолютная температура тела прямо пропорциональна средней кинетической энергии такого движения атомов и молекул. Коэффициент пропорциональности — Постоянная Больцмана.

 

Литература

· Вейль Г. Пространство. Время. Материя. Лекции по общей теории относительности. — М.: изд-во УРСС научной и учебной литературы, 2004. — 455 с.

· Дирак П. А. М. Общая теория относительности. — М.: Атомиздат, 1978.

· Фок В. А. Теория пространства, времени и тяготения. — 2-е изд. — М.: ГИФМЛ, 1961.

· Толмен Р. Относительность, термодинамика и космология. — М.: Наука, 1974.

· Пенроуз Р. Структура пространства-времени. — М.: Мир, 1972.

· Мизнер Ч., Торн К., Уилер Дж. Гравитация. — М.: Мир, 1977. — Т. 1.

· Мизнер Ч., Торн К., Уилер Дж. Гравитация. — М.: Мир, 1977. — Т. 2.

· Мизнер Ч., Торн К., Уилер Дж. Гравитация. — М.: Мир, 1977. — Т. 3.

· Хокинг С., Эллис Дж. Крупномасштабная структура пространства-времени. — М.: Мир, 1977.

· Визгин В. П. Релятивистская теория тяготения (истоки и формирование, 1900—1915). — М.: Наука, 1981. — 352 с.

· Визгин В. П. Единые теории в 1-й трети ХХ века. — М.: Наука, 1985. — 304 с.

· Фейнман Р. Ф., Мориниго Ф. Б., Вагнер У. Г. Фейнмановские лекции по гравитации / Пер. с англ. А. Ф. Захарова. — М.: Янус К, 2000. — 296 с. — ISBN 5-8037-0049-5.

· Вайнберг С. Гравитация и космология / Пер. с англ. В. М. Дубовика и Э. А. Тагирова, под ред. Я. А. Смородинского. — Волгоград: Платон, 2000. — 696 с. — ISBN 5-8010-0306-1.

· Чудинов Э. М. Теория относительности и философия. — М.: Политиздат, 1974. — 304 с.

· Паули В. Теория относительности. — М.: Наука, 1983. — 336 с.

· Вейль Г. Математическое мышление. — М.: Наука, 1989. — 400 с. — ISBN 5-02-013910-6.