Определение средней плотности образцов правильной геометрической формы

 

Средняя плотность – масса единицы объема материала в естественном состоянии, т.е. вместе с порами и пустотами. Средняя плотность ρ₀ (г/см³, кг/м³) вычисляется по формуле

ρ₀ = m / V₀, (4)

 

где m – масса материала; V₀ – объем материала в естественном состоянии.

Для определения плотности* используют образцы материала в форме куба, параллелепипеда или цилиндра.

Штангенциркулем измеряют образцы с точностью до 0,1 мм, и вычисляют их объем, после чего взвешивают на технических весах. Каждую грань образца кубической или близкой к ней формы измеряют в трех местах, как показано на рис.2а. За окончательный результат принимают среднее арифметическое трех измерении каждой грани. На каждой из параллельных плоскостей образца цилиндрической формы проводят два взаимно перпендикулярных диаметра (d₁, d₂, d₃, d₄) и измеряют их длину; кроме того, измеряют диаметры средней части цилиндра (d₅, d₆) в середине его высоты (рис.2б). За окончательный результат принимают среднее арифметичес­кое шести измерений диаметра. Высоту цилиндра определяют в четырех местах (h₁, h₂, h₃, h₄) и за окончательный ре­зультат принимают среднее арифметическое четырех измере­ний.

Образцы любой формы со стороной размером до 100 мм измеряют с точностью до 0,1 мм, размером 100 мм и более с точностью до 1 мм. Образцы массой менее 500 г взвеши­вают с точностью до 0,1 г, а массой 500 г и более - с точ­ностью до 1 г.

Объем образца (см³ ), имеющего вид куба или параллеле­пипеда:

(5)

где а_ср , b_ср , h_ср - средние значения размеров граней об­разца, см.

Объем образца цилиндрической формы (см³)

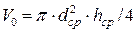, (6)

где π =3,14;d_ср ^_ средний диаметр цилиндра, см; h_ср ^_ сред­няя высота цилиндра, см.

 

_______________________________________________

*Для краткости допускается вместо термина «средняя плотность» применять термин «плотность».

 

 

Зная объем и массу образца, по формуле (4) вычисляют его плотность как среднее арифметическое трех ее значений различных образцов.

 

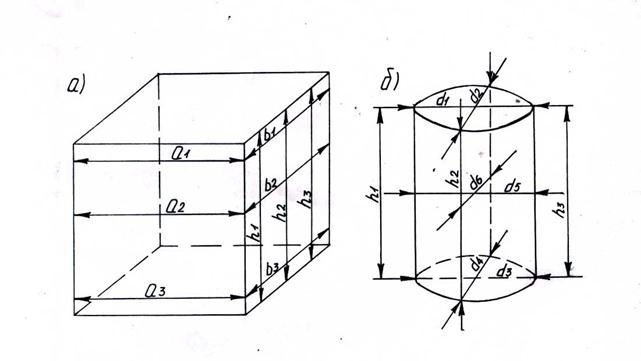
Рис.2. Схемы измерения объема образцов правильной геометрической формы

Полученные результаты:

 

Вывод: