Практические способы расчета случайных погрешностей
Математическая обработка результатов измерений является весьма трудоемким делом, зачастую отнимающим больше времени, чем сами измерения. Она требует внимания и аккуратности. Задача упрощается, если пользоваться соответствующими алгоритмами, которые представляют собой план рациональной последовательности действий при нахождении результата и его погрешности.
§ 1. Обработка прямых измерений (алгоритм прямых измерений).
Пусть искомая величина x измерена n раз, для нахождения 
и 
, рекомендуется записать данные в следующую таблицу и производить расчеты в указанном порядке.
Таблица 1
| № | xi | xi -
| (xi - )2
|
| x1 | x1 -
| (x1 - )2
| |
| x2 | x2 -
| (x2 - )2
| |
| x3 | x3 -
| (x3 - )2
| |
| … | ….. | …… | ………. |
| n | xn | xn -
| (xn -)2
|
| 
|
1. Найти сумму всех xi ( )
2. Найти = 
3. Заполнить третий и четвертый столбцы таблицы.
4. Сосчитать сумму в четвертом столбце
5. Рассчитать среднеквадратичную погрешность среднего арифметического, используя полученную в четвертом столбце сумму. 
6. Найти в «таблице коэффициентов Стьюдента» tn-1,P для данного числа измерений и выбранной вероятности.
7. Определить 
8. Записать окончательный результат 
.
Пример. Пять раз измерен диаметр проволоки с помощью микрометра. Получены следующие результаты (столбец 2).
Таблица 2
| № | di, мм | di-  ,мм
| (di- )2,
|
| 3,90 | 0,01 | 1  10-4
| |
| 3,85 | -0,06 | 36 10-4
| |
| 3,88 | -0,03 | 9 10-4
| |
| 3,97 | 0,06 | 36 10-4
| |
| 3,95 | 0,04 | 16 10-4
| |
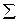
| 19,55 | 98 10-4
|
=19,55 / 5 =3,910 мм
Для доверительной вероятности Р=0,95 и числа измерений n=5, коэффициент Стьюдента 
=3,2, тогда
=3,2 0,022= 0,070 мм.
Окончательный результат: = (3,91±0,07 P=0,95 ) мм.
Относительная погрешность dd = (0,07 / 3,91) 100% = 1,8%.
Возможны другие способы расчета, смотри приложение §§ 4,5.
§ 2. Обработка косвенных измерений. Функция одной переменной. (Формулы переноса ошибок).
Пусть искомая физическая величина Y является функцией измеряемой величины x.
Y =f(x)
Так как величина x не может быть определена абсолютно точно, то и рассчитанное значение Y будет содержать погрешность. Значение искомой функции следует находить, как функцию среднего арифметического значения измеренной величины 
, то есть в формулу для ее определения подставить вычисленное среднее значение
Как определить погрешность функции, если известна погрешность аргумента?
Для этого пользуются известным соотношением между дифференциалом функции df(x)и бесконечно малым приращением аргумента dx:
Полагая Dx»dx, а DY»dY , получаем выражение для погрешности функции:
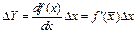
| (17) |
где Dx =tp,n-1 Sx , 
- производная функции 
при x = .
Иногда оказывается удобнее (проще) вычислить сначала относительную погрешность, а уже зная ее, определить доверительный интервал. Учитывая то, что: 
легко видеть, что относительную погрешность функции можно вычислить, воспользовавшись следующей формулой:
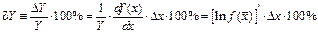
| (18) |
§ 3 Обработка косвенных измерений. Функция многих переменных. (Формулы переноса ошибок)
В общем случае искомая физическая величина может быть функцией не одной, а нескольких измеряемых величин, то есть: Y= f(X1, X2,…Xn)* Каждая из величин X1, X2,…Xn определяется с соответствующей погрешностьюDX1, DX2,… DXn. В этом случае средняя квадратичная погрешность функции будет равна корню квадратному из суммы квадратов частных производных функции по всем независимым переменным, домноженным на среднеквадратичную погрешность соответствующей величины:
| (19) |
В данной формуле каждая скобка под корнем представляет собой вклад погрешности соответствующей величины в погрешность функции. Если погрешности различных измеряемых величин определены с одной и той же доверительной вероятностью, то формулу можно переписать в следующем виде:
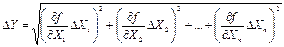
| (20) |
Относительная погрешность функции может быть вычислена по формуле:
| (21) |
Приведенные формулы справедливы для любых функциональных зависимостей, однако, они довольно громоздки, производить по ним расчеты бывает достаточно сложно, они требуют больших затрат времени. В некоторых случаях бывает удобнее использовать выражения, преобразованные для частных случаев функциональной зависимости. Рассмотрим несколько таких частных случаев.
Погрешность алгебраической суммы
Пусть функция имеет вид:
Y = 
, тогда среднеквадратичная погрешность такой функции будет определяться:
| (22) |
а выборочная дисперсия:
| (23) |
То есть выборочная дисперсия алгебраической суммы равна суммевыборочных дисперсий отдельных независимых переменных. Обратите внимание,на то, что в выражение для выборочной дисперсии функции все слагаемые входят со знаком «+», независимо от того, с каким знаком соответствующая величина входила в алгебраическую сумму.
Погрешность произведения.
Пусть функция имеет вид:
или 
В этих случаях, воспользовавшись формулой (21) и, учитывая то, что логарифм произведения равен сумме логарифмов, получаем выражение для относительной погрешности функции:
| (24) |
То есть относительная погрешность произведения (и частного) равна корню квадратному из суммы квадратов относительных погрешностей всех сомножителей. Также как и в случае суммы, обратите внимание, на то, что все слагаемые под корнем берутся со знаком «+», независимо от того в числитель или знаменатель выражения функции они входили.
Производить расчет по этой формуле обычно гораздо проще, чем по формуле (19), а доверительный интервал искомой величины легко найти: 
.
Погрешности некоторых элементарных функций.
1. 
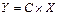, где С=const; 
2. 
; 
3. 
; 
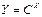§ 4. Два способа оценки погрешности при косвенных измерениях.
В случае косвенных измерений физических величин возможны два способа вычисления окончательного результата и погрешности.
Первый способ.
Для каждой измеряемой физической величины проводят серию измерений. Эти измерения (прямые) обрабатывают и находят средние значения 
и соответствующие им доверительные интервалы 
с одной и той же доверительной вероятностью. Затем по выражению функциональной зависимости Y= f (X1,X2,…Xn) находят среднее значение искомой физической величины, используя найденные средние значения всех измеренных величин 
. Затем по формулам переноса ошибок (формула 19 или ее частные случаи) рассчитывают доверительный интервал величины Y.
Пример
Задача - определить ускорение свободного падения с помощью математического маятника.
Формула для расчета - 
, где l - длина маятника, T - период его колебаний.
Измерили 5 раз длину маятника и 5 раз его период. Получили следующие значения, которые обработали, как прямые измерения:
Таблица 3
| l(м) |  (м)
| 
|  0,9644
 =0,00051
D3,2´0,00051=0,0016
| |||
| 0,965 | 0,0006 | 3,6 ´10-7 | ||||
| 0,966 | 0,0016 | 25,6´10-7 | ||||
| 0,964 | -0,0004 | 1,6´10-7 | ||||
| 0,963 | -0,0014 | 19,6´10-7 | ||||
| 0,964 | -0,0004 | 1,6´10-7 | ||||
| S | 4,822 | 52´10-7 | ||||
| Т(сек) | Т- 
| (Т-  )2
|  1,9698
=0,000583
D 3,2´ 0,000583 =0,001866»0,0019
| |||
| 1,970 | 0,0002 | 0,04´10-6 | ||||
| 1,969 | -0,0008 | 0,64´10-6 | ||||
| 1,971 | 0,0012 | 1,44´10-6 | ||||
| 1,968 | -0,0018 | 3,24´10-6 | ||||
| 1,971 | 0,0012 | 1,44´10-6 | ||||
| S | 9,849 | 6,8´10-6 | ||||
Получили: 0,9644 и 1,9698.
Затем рассчитывают 
и, в соответствии с формулой (7) рассчитывают относительную погрешность g:
.
Тогда Dg = g ´dg =9,812342 ´ 0,0025=0,0249 » 0,025, и окончательный результат, соответственно: 
(9,812±0,025) м/с2 при Р=0,95
Второй способ.
В случаях, когда по условиям опыта измерения делаются в не воспроизводимых условиях, значения функции, Y= f(X1,X2,…Xn) вычисляют для каждой отдельной серии измерений {Xi}, а затем полученный ряд значений Yi , обрабатывают по алгоритму прямых измерений.
Пример
Пусть поставлена та же задача - определить g, но при этом имеется несколько (пять) заведомо различных маятников. В этом случае рационально поступить следующим образом. Для каждого маятника измерить его длину и период колебаний. По этим значениям рассчитать величину g (для каждого маятника независимо). Полученные значения g обработать, как прямые измерения.
Таблица 4
| № маятника | L(м) | Т(сек) | g (м/с2) | 
| 
|
| 0,965 | 1,970 | 9,816453 | 0,00355 | 0,126032´10-4 | |
| 1,222 | 2,222 | 9,771086 | -0,041817 | 17,48669´10-4 | |
| 1,568 | 2,510 | 9,825584 | 0,01268 | 1,60795´10-4 | |
| 0,559 | 1,498 | 9,834401 | 0,0215 | 4,62167´10-4 | |
| 0,752 | 1,739 | 9,816991 | 0,00409 | 0,167152´10-4 | |
| S | 49,06452 | 24,0095´10-4 |
,
Dg = 3,2´0,01096 =0,035
и, соответственно, окончательный результат:
(9,813±0,035) м/с2 при Р=0,95
§ 5 Метод наименьших квадратов (МНК).
Помимо двух вышеописанных способов оценки погрешности результата при косвенных измерениях, иногда применяют еще так называемый «метод наименьших квадратов» или сокращенно МНК. Этот метод можно использовать, если известен вид функциональной зависимости между измеряемыми физическими величинами, а требуется определить коэффициенты, входящие в эту функцию. В наших лабораторных работах предлагается применять этот метод для определения параметровлинейной зависимости.
Пусть в эксперименте можно измерить ряд значений некоторой величины x и, соответствующие им значения, величины y. И пусть при этом известно, что между ними справедлива зависимость вида: y = ax + b. Как известно, такая зависимость графически представляется прямой линией (рис.4). Однако измеренные значения xi и yi включают в себя погрешность и, в результате, не лягут идеально на прямую линию.
Как по данным экспериментальных наблюдений наилучшим образом найти коэффициенты a и b? Графически эта задача сводится к построению прямой, ближе всего лежащей ко всем экспериментальным токам, так как прямая однозначно задается этими коэффициентами(рис.4.).
| Для аналитического выражения коэффициентов применяется метод наименьших квадратов. Утверждается, что наилучшей будет та прямая, сумма квадратов расстояний до которой, от всех экспериментальных точек будет минимальной. Расстояние (вдоль оси y) от точки с координатами xi, yi до искомой прямой определяется выражением: (axi +b -yi), |
| Рис.4 |
тогда сумма квадратов расстояний будет равна:
Решение задачи на нахождение минимума этого выражения (см. приложение, § 7) приводит к следующим выражениям для коэффициентов a и b.
| (25) |
| (26) |
Дисперсию отклонения экспериментальных точек от прямой - S02 и дисперсию коэффициентов a и b - Sa2 и Sb2 можно вычислить по формулам:
