Пример выполнения работы

 

Для наилучшей (3-й) партии было определено s²=0,00042, s=0,021, 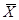=29,669, n=50.

 

1. Доверительный интервал для мат. ожидания:

 

k=50-1=49;

γ=0,99; α=1-0.99=0.01; t=2,679; ε=2,679*0,021/7,071=0.008;

29,661< 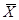<29,677

γ=0,95; α=1-0.95=0.05; t=2,009. ε=2,009*0,021/7,071=0.006.

29,663< 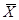<29,675

 

2. Доверительный интервал для оценки дисперсии:

 

γ=0,99; q=0.30; (1-0,30)*0,021<σ<(1+0,30)*0,021;

0,0147<σ<0,0273

γ=0,95; q=0,21. (1-0,21)*0,021<σ<(1+0,21)*0,021;

0,0166<σ<0,0254

 

3. s=0,021; ε=0,0063; t=ε* =0,0063*7,071/0,021=2,12;

Для t=2,12 и доверительной вероятности 0,95 находим k=16; n=k+1=17.

 

4. q=σ/s-1=1,5-1=0,5; Для вероятности 0,95 и q=0,5, n=14.

РАСЧЕТНАЯ РАБОТА №4

 

ПРОВЕРКА ГИПОТЕЗЫ О НОРМАЛЬНОСТИ РАСПРЕДЕЛЕНИЯ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ. КРИТЕРИИ ПИРСОНА И КОЛМОГОРОВА

 

Для выбранного в расчетной работе №1 товара:

1. Проверить гипотезу о нормальности распределения с помощью критерия согласия Пирсона при уровне значимости a=0,01 и a=0,05.

2. Проверить гипотезу о нормальности распределения с помощью критерия λ Колмогорова при уровне значимости a=0,05.