Пример выполнения работы

Имеется три партии товара, основной размер которого D=29,67мм. Максимально допустимое верхнее отклонение ВО=0,07мм, Максимально допустимое нижнее отклонение НО=-0,07мм. Из каждой партии взята выборка, объема n=50 штук. Детали из выборки измерены прибором с ценой деления 0,01<0,1∙2δ, где 2δ=ВО-НО=0,14 – допуск, и результаты измерения x₁, x₂ и x₃ представлены ниже.

Необходимо определить наиболее соответствующую требованиям партию, применив следующие критерии оценки:

Оценка мат. ожидания 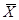наиболее близка к требуемому размеру D.

Разброс параметров товара (среднеквадратическое отклонение) минимально.

Вероятность выхода из интервала допустимых отклонений минимальна.

Выборочные значения партий товаров:

x_1i: 29,63; 29,65; 29,63; 29,63; 29,63; 29,69; 29,64; 29,65; 29,7; 29,63; 29,69; 29,67; 29,61; 29,64; 29,64; 29,67; 29,64; 29,64; 29,65; 29,69; 29,62; 29,67; 29,67; 29,64; 29,68; 29,64; 29,65; 29,7; 29,63; 29,65; 29,65; 29,63; 29,63; 29,63; 29,63; 29,61; 29,69; 29,67; 29,65; 29,69; 29,63; 29,66; 29,66; 29,66; 29,7; 29,66; 29,68; 29,68; 29,67; 29,67

x_2i: 29,71; 29,65; 29,65; 29,66; 29,69; 29,7; 29,69; 29,68; 29,66; 29,68; 29,7; 29,67; 29,68; 29,71; 29,63; 29,69; 29,69; 29,71; 29,67; 29,69; 29,73; 29,7; 29,66; 29,72; 29,68; 29,69; 29,68; 29,67; 29,72; 29,68; 29,68; 29,63; 29,65; 29,68; 29,69; 29,65; 29,68; 29,73; 29,65; 29,7; 29,7; 29,69; 29,71; 29,67; 29,7; 29,68; 29,66; 29,65; 29,68; 29,66

x_3i:29,68; 29,64; 29,66; 29,64; 29,67; 29,69; 29,64; 29,71; 29,65; 29,67; 29,67; 29,66; 29,68; 29,65; 29,7; 29,66; 29,7; 29,66; 29,68; 29,66; 29,65; 29,67; 29,66; 29,67; 29,63; 29,67; 29,63; 29,67; 29,65; 29,71; 29,68; 29,69; 29,7; 29,65; 29,69; 29,68; 29,68; 29,66; 29,7; 29,69; 29,69; 29,65; 29,68; 29,67; 29,64; 29,65; 29,67; 29,65; 29,68; 29,69

1. По результатам составить таблицу распределения значений деталей выборки.

а) Цена разряда c=(x_max-x_min)/m, x_max – максимальное наблюденное значение, x_min – минимальное наблюденное значение, m – число интервалов, для n=50, m=7. Проверить, с>цены деления прибора. В случае необходимости пересчитать.

m=7;

x_{1 min}=29,61; x_{1 max}=29,7;

с₁=(29,7-29,61)/7=0,0128>0,01

x_{2 min}=29,63; x_{2 max}=29,73;

с₂=(29,73-29,63)/7=0,0142>0,01

x_{3 min}=29,63; x_{3 max}=29,71;

с₃=(29,71-29,63)/7=0,0114>0,01;

б) Подсчитать частоты f_i и относительные частоты m_i=f_i/n наблюденных значений по интервалам. Результаты занести в таблицу.

x_{1 i min}	x_{1 i max}	x_{1 i}	f_{1 i}	m_{1 i}
29,61	29,623	29,616		0,06
29,623	29,636	29,629		0,22
29,636	29.649	29,642		0,14
29.649	29.661	29,655		0,22
29.661	29.674	29,668		0,14
29.674	29.687	29,681		0,06
29.687	29.7	29,694		0,16

x_{2 i min}	x_{2 i max}	x_{2 i}	f_{2 i}	m_{2 i}
29,63	29,644	29,637		0,04
29,644	29,659	29,651		0,12
29,659	29.673	29,666		0,18
29.673	29.687	29,68		0,22
29.687	29.701	29,694		0,28
29.701	29.716	29,709		0,08
29.716	29.73	29,723		0,08

x_{3 i min}	x_{3 i max}	x_{3 i}	f_{3 i}	m_{3 i}
29,63	29,641	29,636		0,12
29,641	29,653	29,647		0,16
29,653	29.664	29,659		0,14
29.664	29.676	29,67		0,18
29.676	29.687	29,681		0,16
29.687	29.699	29,693		0,12
29.699	29.71	29,704		0,12

2. Считая, что выборки извлечены из нормально распределенной генеральной совокупности, рассчитать параметры статистического распределения:

а) , , . За x_i принимается середина разряда.

Средние арифметические:

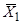=(29,616∙3+29,629∙11+29,642∙7+29,655∙11+29,668∙7+29,68∙3+29,694∙8)/50=29,654

=(29,637∙2+29,651∙6+29,666∙9+29,68∙11+29,694∙14+29,709∙4+29,723∙4)/50=29,682

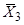=(29,636∙6+29,647∙8+29,659∙7+29,67∙9+29,681∙8+29,693∙6+29,704∙6)/50=29,669.

Выборочные дисперсии и среднеквадратические отклонения:

s₁²=(1/50)((29,616-29,654)²∙3+(29,629-29,654)²∙11+(29,642-29,654)²∙7+(29,655-29,654)²∙11+
+(29,668-29,654)²∙7+(29,68-29,654)²∙3+(29,694-29,654)²∙8)=0,0006;

s₁=0,025;

s₂²=(1/50)((29,637-29,682)²∙2+(29,651-29,682)²∙6+(29,666-29,682)²∙9+(29,68-29,682)²∙11+
+(29,694-29,682)²∙14+(29,709-29,682)²∙4+(29,723-29,682)²∙4)=0,0005;

s₂=0,024;

s₃²=(1/50)((29,636-29,669)²∙6+(29,647-29,669)²∙8+(29,659-29,669)²∙7+(29,67-29,669)²∙9+
+(29,681-29,669)²∙8+(29,693-29,669)²∙6+(29,704-29,669)²∙6)=0,0004;

s₃=0,021;

б) Определить значение σ=(1+q)s, q – коэффициент, определяющий границу доверительного интервала нахождения генеральной дисперсии распределения по найденному выборочному среднеквадратическому отклонению s. q взять из таблицы 4 [3] в зависимости от n.

для n=50 q=0,21:

σ₁=0,031; 3σ₁=0,093; σ₂=0,029; 3σ₂=0,087; σ₃=0,026; 3σ₃=0,078;

в) Построить кривую или гистограмму распределения наблюденных значений. Отметить на ней D, ВО, НО, 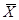и трехсигмовые пределы.

Рис. 1. Гистограммы распределения выборочных значений

Вывод: очевидно, что первая выборка имеет существенное отклонение от требуемого размера, по сравнению с остальными, и может быть исключена из дальнейшего рассмотрения. Для двух оставшихся выборок необходимо произвести более точный анализ.

3. Определить вероятность получения брака.

а) Смещение оценки математического ожидания от требуемого размера:

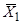| -D|=|29,65-29,67|=0,02

| -D|=|29,68-29,67|=0,01

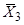| -D|=|29,67-29,67|=0;

б) Вероятный процент брака q=[0,5-Ф((δ-(| 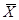-D|))/σ)]∙100%.

q₁=[0,5-Ф((0,07-0,02)/0,031)]∙100%=[0,5-Ф(1,61)]∙100%=5,37%

q₂=[0,5-Ф((0,07-0,01)/0,029)]∙100%=[0,5-Ф(2,07)]∙100%=1,93%

q₃=[0,5-Ф((0,07-0)/0,026)]∙100%=[0,5-Ф(2,69)]∙100%=0,36%.

4. Сделать вывод.

Наименьший процент брака у третьей партии. Оценка мат. ожидания 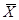наиболее близка к требуемому размеру D у третьей партии. Среднеквадратическое отклонение наименьшее также у третьей партии. Следовательно, третья партия наилучшим образом соответствует требованиям.