Взаимное расположение плоскостей.

1.2.1. Пусть плоскости П₁: A₁x+B₁y+C₁z+D₁=0 и П₂: A₂x+B₂y+C₂z+D₂=0 заданы своими общими уравнениями. Тогда:

а) они параллельны тогда и только тогда, когда 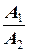= = 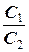, при этом они совпадают тогда и только тогда, когда это отношение равно и не совпадают тогда и только тогда, когда это отношение не равно ;

б) они перпендикулярны тогда и только тогда, когда A₁A₂+B₁B₂+D₁D₂=0.

1.2.2. Из 1.2.1 следует, что если выполнено хотя бы одно из условий 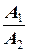≠ , 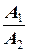≠ 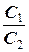, ≠ 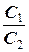, то плоскости П₁ и П₂ пересекаются по бесконечному множеству точек, которые образуют прямую.

1.2.3. Если плоскости П₁ и П₂ заданы своими общими уравнениями (см. 1.2.1), то угол между ними можно найти из соотношения

cos( 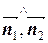)= , (1.7)

где =(A₁, B₁, С₁), =(A₂, B₂, С₂) .

1.2.4. Упражнение. Выяснить взаимное расположение плоскостей:

а) П₁: 2x-3y+4z+4=0; П₂: 4x-6y+8z+8=0; П₃: 6x-9y+12z+5=0;

П₄: 5x+2y-z-5=0; П₅: x+2y-3z+4=0;

б) П₁: 4x-3y-5z+2=0; П₂: 3x+4y-8=0; П₃: 2x+y+8z-2=0;

П₄: 8x+4y+32z+12=0; П₅: 8x+4y+32z-8=0.

В случае, когда плоскости ни параллельны, ни перпендикулярны, найти угол между ними.

Решение. а) П₁ и П₂: 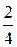= = = . Поэтому плоскости П₁ и П₂ совпадают.

П₁ и П₃: 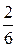= = ≠ . Поэтому плоскости П₁ и П₃ параллельны, но не совпадают.

П₁ и П₄: 2×5+(-3)×2+4×(-1)=0. Поэтому плоскости П₁ и П₄ перпендикулярны.

П₁ и П₅: ≠ и 2×1+(-3)×2+4×(-3)≠0. Поэтому плосксти ни параллельны, ни перпендикулярны. Найдём угол между ними. Имеем (по формуле (1.7))

cos( )=cos( 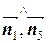)= = »0,7941.

Тогда ( )»arccos0,7941»0,65 (радиан).

Аналогично исследуется взаимное расположение пар плоскостей (П₂, П₃), (П₂, П₄), (П₂, П₅), (П₃, П₄), (П₃, П₅), (П₄, П₅) (довести до конца!).

Ответ: а) Плоскости П₁ и П₂ совпадают, П₁ и П₃ - параллельны и не совпадают, плоскостиП₁ и П₄ перпендикулярны, угол между плоскостямиП₁ и П₅ равен »1,05 радиан.