Упражнения.

1) Относительно системы координат написать уравнения прямых, которые проходят через точку N(4; -1) и:

- параллельна прямой l₁;

- перпендикулярна прямой l₂;

- образует угол a с прямой l₃:

а) l₁: 2x-5y+8=0; l₂: 3x+y-6=0; a= , l₃: y=5x+6;

б) l₁: x+8y-5=0; l₂: -6x+y+3=0; a= 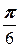, l₃: y=4x-8.

Решение. а) Найдём уравнение прямой, параллельной l₁.

I способ. Если прямая l: Ax+By+C=0 параллельна l₁: 2x-5y+8=0, то = . Можно считать, что A=2 и B=5, то есть 2x-5y+C=0. Так как l проходит через точку N(4; -1), то координаты N удовлетворяют уравнению прямой: 2×4-5×(-1)+C=0. Отсюда C=-13. Следовательно, 2x-5y-13=0 - искомое уравнение прямой.

II способ. Если прямые параллельны, то их перпендикуляр - общий. В частности, их нормаль общая, то есть =(2; -5) - общая нормаль для искомой прямой и l₁. Поэтому уравнение искомой прямой - 2(x-4)-5(y+1)=0, или 2x-5y-13=0.

Найдём уравнение прямой, перпендикулярной l₂. Ясно, что нормаль для l₂ является направляющей для искомой. Поэтому = - искомое уравнение.

Для нахождения уравнения прямой, убразующей угол с прямой y=5x+6, напишем его уравнение в общем виде: 5x-y+6=0. Пусть l: Ax+By+C=0 - искомая прямая (уравнение прямой). Можно считать, что A=1 (если это не так, то уравнение делим на A). Поэтому

cos( )= =

(в качестве угла между прямыми берём острый угол, и тогда знаки модуля можно опускать). Так как ( )= , то cos( )=cos = и приходим к уравнению = , которое решаем:

= Û 10-2B= Û 100-40B+4B²=52+52B² Û

Û 48B²+40B-48=0 Û 6B²+5B-6=0.

Решаем последнее квадратное уравнение:

D=52-4×6×(-6)=169, B_{1, 2}= = , B₁=- , B₂= .

Таким образом, x- y+C=0 и x+ y+C=0 или, соответственно 2x-3y+2C=0 и 3x+2y+3C=0 - уравнения искомых прямых. Найдём C для обоих уравнений: 2×4-3×(-1)+2C=0, откуда C=- , и 3×4-2×(-1)+2C=0, откуда C=-7. Таким образом, 2x-3y-11=0 и 3x+2y-14=0 - искомые уравнения прямых.

Ответ: а) 2x-5y-13=0 - уравнение прямой, проходящей через точку N(4; -1) и параллельной l₁;

= - уравнение прямой, проходящей через точку N(4; -1) и перпендикулярной l₂;

2x-3y-11=0 и 3x+2y-14=0 - уравнения прямых, образующих угол с прямой l₃ и проходящей через точку N(4; -1).

2) Даны вершины треугольника ABC. Составить: уравнения сторон треугольника; уравнения прямых, параллельных сторонам и проходящих через вершины треугольника; уравнения высот. Найти длины высот:

а) A(3; 2), B(4; -1), С(2; 8);

б) A(1; 2), B(2; 1), С(2; 8);

Решение. а) Уравнения сторон будем искать как уравнения прямых, проходящих через (две) вершины. Найдём уравнение стороны AB:

= Û = ,

то есть = - уравнение стороны AB (в каноническом виде). Напишем уравнение прямой, проходящей через вершину C параллельно стороне AB. Ясно, что вектор =(1; -3) является направляющим для этой прямой. Поэтому её уравнение: = .

Напишем уравнение высоты, опущенной из вершины C. Эта высота перпендикулярна стороне AB, то есть вектор является нормалью для этой высоты. Поэтому её уравнение x+2-3(y+8)=0 Û x-3y-22=0.

Длину высоты h_c, опущенной из вершины C будем искать как расстояние от точки C до прямой AB. Для этого уравнение прямой AB приведём к общему виду:

= Û -3(x-3)=y-2 Û -3x-y+11=0 Û 3x+y-11=0.

Тогда

h_c=r(C, AB)= = = .

Аналогично находятся остальные прямые и длины высот (требуемые по условию задачи) (довести до конца!)

Ответ: а) = , 3x+y-11=0 - уравнения стороны AB;

= - уравнение прямой, проходящей через вершину C параллельно стороне AB;

x-3y-22=0 - уравнение высоты, опущенной из вершины C;

- длина высоты, опущенной из вершины C.