Транспортная задача.
Транспортная задача (ТЗ) – частный случай задачи линейного программирования. В ТЗ существуют поставщики и потребители грузов. У каждого поставщика имеется определенное количество груза – мощность поставщика, а каждому потребителю нужно определенное количество груза – спрос потребителя. Известны затраты на перевозку единицы груза. Нужно составить такой план перевозок, при котором суммарные затраты на перевозку груза будут минимальными, по возможности будут задействованы все мощности поставщика и удовлетворен весь спрос потребителей.
Модель задачи.
Введем следующие переменные.
ai – мощность поставщика (предложения продукта в пункте i=1,…,n), n – количество поставщиков.
bj – спрос потребителя (в пункте j=1,…,m), m – количество потребителей.
cij - затраты на перевозку единицы продукции из пункта i в пункт j.
xij - количество груза, перевозимого из пункта i в пункт j.
В этих обозначениях транспортную задачу можно записать следующим образом.
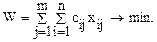

Закрытая модель ТЗ (сбалансированная модель) – модель, в которой суммарная мощность поставщиков равна суммарному спросу потребителей.
Общий спрос равен общему предложению (мощности всех поставщиков).

Открытая модель ТЗ (не сбалансированная модель) – модель, в которой суммарная мощность поставщиков не равна суммарному спросу потребителей.

В процессе решения открытая модель всегда сводится к закрытой. Вводится фиктивный потребитель (что бы убрать неравенство) с недостающим спросом, но стоимость перевозок для него равна нулю (не меняет целевую функцию). Если суммарная мощность поставщиков меньше суммарного спроса потребителя, то вводится фиктивный поставщик, также получается закрытая модель, которая решаема.
Алгоритм решения закрытой модели ТЗ:
Составляется специальная таблица поставщиков и потребителей с указанием их мощностей и спросов;
Находим первоначальный план поставок. Существует несколько методов построения плана:
- метод северо-западного угла;
- метод минимальной стоимости;
- метод потенциалов.
Оптимизируем план распределительным методом.
Алгоритм рассмотрим на конкретном примере.
Имеется 4 поставщика А и 5 потребителей В. Мощности поставщиков и спрос потребителей, а также затраты на перевозку единицы груза для каждой пары поставщик-потребитель сведены в таблицу поставок:
Таблица3
 Потр
Пост Потр
Пост
| В1 | В2 | В3 | В4 | В5 | Мощ- ноть ai |
| А1 | ||||||
| А2 | ||||||
| А3 | ||||||
| А4 | ||||||
| Спрос bj |
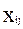 – искомый объем поставок i-го поставщика j-ому потребителю (
– искомый объем поставок i-го поставщика j-ому потребителю (  ).
).
Запишем ограничения (уравнения баланса для каждой строки таблицы поставок):

Уравнения баланса для каждого столбца таблицы поставок:

Целевая функция - суммарные затраты W  на перевозку выражается через коэффициенты затрат
на перевозку выражается через коэффициенты затрат
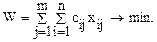
Будем называть любой план перевозок допустимым, если он удовлетворяет выше обозначенным условиям – все заявки удовлетворены, все запасы исчерпаны.
План (хij)будем называть оптимальным, если он, среди всех допустимых планов, приводит к минимальной суммарной стоимости перевозок W = min.
В силу особой структуры ТЗ (системы условий имеют единичные коэффициенты) при ее решении не приходится долго решать систему уравнений. Все операции по нахождению оптимального плана сводятся к манипуляциям непосредственно с таблицей, где в определенном порядке записаны условия транспортной задачи: перечень поставщиков и потребителей, спрос и мощности, а также стоимости перевозок.
По мере заполнения этой таблицы в ее клетках проставляются сами перевозки хijТранспортная таблица состоит из тстрок и пстолбцов. В каждой клетке мы будем ставить стоимость перевозки единицы груза из Ав В (правый верхний угол), а центр клетки оставим свободным, чтобы помещать в нее саму перевозку хi,j. Клетку таблицы, соответствующую пунктам А и Вбудем кратко обозначать (i,j).
Прежде всего займемся составлением допустимого плана. Это в транспортной задаче очень просто: можно, например, применить так называемый «метод северо-западного угла».
Таблица 4
 ПОТ
ПОСТ ПОТ
ПОСТ
| В1 | В2 | В3 | В4 | В5 | Мощность ai |
| А1 | 1813 | 12 7 | ||||
| А2 | 15 8 |   33 12 33 12
|  8 8
| |||
| А3 |  910 910
| 118 | ||||
| А4 | 410 | 2615 | ||||
| Спрос bj |
Начнем заполнение транспортной таблицы с левого верхнего угла. Пункт В1подал заявку на 18 единиц груза; удовлетворим ее из запасов пункта А1.После этого в нем остается еще 30 — 18 = 12 единиц груза; отдадим их пункту В2. Но заявка этого пункта еще не удовлетворена; выделим недостающие 15 единиц из запасов пункта А2и т. д. Рассуждая точно таким же образом, заполним до конца перевозками хijтранспортную таблицу (таблица 5).
Проверим, является ли этот план допустимым. Да, потому что в нем сумма перевозок по строке равна запасу соответствующего пункта отправления, а сумма перевозок по столбцу — заявке соответствующего пункта назначения (все заявки удовлетворены, все запасы израсходованы). Сумма запасов равна сумме заявок и выражается числом 128, стоящим в правом нижнем углу таблицы.
Проверим, является ли этот план допустимым. Да, потому что в нем сумма перевозок по строке равна запасу соответствующего пункта отправления, а сумма перевозок по столбцу — заявке соответствующего пункта назначения (все заявки удовлетворены, все запасы израсходованы). Сумма запасов равна сумме заявок и выражается числом 128, стоящим в правом нижнем углу таблицы.
Здесь и в дальнейшем мы проставляем в таблице только отличные от нуля перевозки, а клетки, соответствующие нулевым перевозкам, оставляем «свободными.
Проверим, можно ли таким планом пользоваться? Является ли система уравнений (ограничений – условий) совместной. Число свободных клеток с нулевыми перевозками в таблице должно быть равно (т — 1)(п — 1) = 3х4 = 12. Если не так, то меняют угол, или меняют метод. При выполнении этого условия план называют опорным.
Теперь проверим план на оптимальность, т. е. минимальна ли для него общая стоимость перевозок?Скорее всего, нет (ведь составляя план, мы совсем не думали о стоимостях). Так и есть — план не оптимальный. Например, сразу видно, что можно его улучшить, если произвести в нем «циклическую перестановку» перевозок между клетками таблицы, уменьшив перевозки в «дорогой» клетке (2.3) со стоимостью 12, но зато увеличив перевозки в «дешевой» клетке (2.4) со стоимостью 6.
Например, перенесем 11 единиц груза по циклу (2.3) —(2.4) — (3.4) — (2.3) —(2,3). Чтобы план оставался опорным, мы должны заполнить одну из свободных клеток, а одну из занятых освободить. Сколько единиц груза можем мы перенести по циклу? Очевидно, не больше чем 11 единиц (иначе перевозки в клетке (3.4) стали бы отрицательными). В результате циклического переноса допустимый план остается допустимым — баланс запасов и заявок не нарушается.
Таблица 5
  22 12 22 12
| 116
|
 2010 2010
| 8 |
Посмотрим, чего мы добились, сколько сэкономили.
Была стоимость: 33х12+11х8+9х10=574.
Стала стоимость: 22х12+11х6+20х10=530.
Мы уменьшили стоимость перевозок на 44 единицы. Это значение называется отрицательной ценой цикла. Общая стоимость плана составила W=1398
Оптимизация плана перевозок заключается в том, чтобы переносить перевозки по циклам, имеющим отрицательную цену.
В теории линейного программирования доказывается, что при опорном плане для каждой свободной клетки транспортной таблицы существует цикл, и притом единственный.
Таким образом, разыскивая в транспортной таблице свободные клетки (с отрицательной ценой цикла) и перебрасывая по циклу наибольшее возможное количество груза, мы будем все уменьшать стоимость перевозок. План, где не остается ни одной свободной клетки с отрицательной ценой цикла будет являться оптимальным.