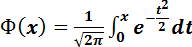КОНТРОЛЬНЫЕ ЗАДАНИЯ.
ВАРИАНТ 1.
1. Брошены две игральные кости. Сколько всего исходов имеет данный опыт? Найти вероятность того, что на каждой кости появилось четное число очков.
2. Из букв разрезной азбуки составлено слово КНИГА. Ребенок, не умеющий читать, рассыпал эти буквы, а затем собрал их в произвольном порядке. Найти вероятность того, что у него получится исходное слово.
3. В «черном» ящике лежат 15 одинаковых на ощупь шаров, 10 из них – белые, остальные – красные. Найти вероятность того, что последовательно вынутые три шара окажутся белыми.
4. В магазине имеется 20 пар обуви одной модели, из них 7 пар 41 размера. Найти вероятность того, что четырем покупателям подряд понадобится именно 41 размер данной модели?
5. Два стрелка одновременно сделали по одному выстрелу в мишень. Вероятность попадания для первого стрелка 0,9, а для второго 0,6. Найти вероятность того, что в мишень попал один стрелок.
6. Три студента сдают экзамен. Вероятность получить положительную оценку для первого студента равна 0,8, для второго – 0,3, для третьего – 0,6. Какова вероятность того, что экзамен будет сдан только одним из студентов?
7. Найти вероятность того, что при четырех подбрасываниях игральной кости 6 очков выпадет два раза.
8. Вероятность работы каждой из четырех снегоуборочных машин без поломок в течение месяца равна 0,8. Составить закон распределения случайной величины X - числа снегоуборочных машин, работавших без поломок. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X.
9. В урне лежат 7 синих и 5 красных шаров. Один за другим из урны вынимают три шара. Составить закон распределения случайной величины X – числа синих шаров в выборке. Найти математическое ожидание случайной величины X.
10. Случайная величина X равномерно распределена в интервале (2;10). Найти: а) дифференциальную функцию случайной величины X; б) интегральную функцию; в) вероятность попадания случайной величины в интервал (4;9); г) математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X.
11. Случайная величина распределена по нормальному закону с математическим ожиданием а = 20 и средним квадратическим отклонением σ=4. Определить вероятность попадания случайной величины в интервал (10; 25).
ВАРИАНТ 2.
1. Брошены две игральные кости. Сколько всего исходов имеет данный опыт? Найти вероятность того, что хотя бы на одной кости появилось три очка.
2. Из букв разрезной азбуки составлено слово КАВКАЗ. Ребенок, не умеющий читать, рассыпал эти буквы, а затем собрал их в произвольном порядке. Найти вероятность того, что у него получится исходное слово.
3. В «черном» ящике лежат 15 одинаковых на ощупь шаров, 10 из них – белые, остальные – красные. Найти вероятность того, что последовательно вынутые три шара окажутся красными.
4. В магазине имеется 20 пар обуви одной модели, из них 10 пар 38 размера. Найти вероятность того, что четырем покупателям подряд понадобится именно 38 размер данной модели?
5. Два стрелка одновременно сделали по одному выстрелу в мишень. Вероятность попадания для первого стрелка 0,9, а для второго 0,6. Найти вероятность того, что в мишень попал хотя бы один стрелок.
6. Три студента сдают экзамен. Вероятность получить положительную оценку для первого студента равна 0,8, для второго – 0,3, для третьего – 0,6. Какова вероятность того, что экзамен будет сдан двумя студентами?
7. Найти вероятность того, что при восьми подбрасываниях монеты решка появится три раза.
8. Вероятность рождения мальчика равна 0,6. Составить закон распределения случайной величины X - числа мальчиков в семьях, имеющих четырех детей. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение.
9. В группе из 12 спортсменов 4 мастера спорта. Составить закон распределения случайной величины X - числа мастеров спорта из трех случайным образом отобранных спортсменов. Найти математическое ожидание случайной величины X.
10. Случайная величина X равномерно распределена в интервале (-4;3). Найти: а) дифференциальную функцию случайной величины X; б) интегральную функцию; в) вероятность попадания случайной величины в интервал (-1;2); г) математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X.
11. Нормально распределенная случайная величина X задана дифференциальной функцией f(x). Определить вероятность попадания случайной величины в интервал (3; 9).

ВАРИАНТ 3.
1. Брошены две игральные кости. Сколько всего исходов имеет данный опыт? Найти вероятность того, что сумма очков на костях – нечетное число.
2. Из букв разрезной азбуки составлено слово РАДУГА. Ребенок, не умеющий читать, рассыпал эти буквы, а затем собрал их в произвольном порядке. Найти вероятность того, что у него получится исходное слово.
3. В «черном» ящике лежат 15 одинаковых на ощупь шаров, 10 из них – белые, остальные – красные. Найти вероятность того, что последовательно вынутые четыре шара окажутся белыми.
4. В магазине имеется 20 пар обуви одной модели, из них 7 пар 39 размера. Найти вероятность того, что трем покупателям подряд понадобится именно 39 размер данной модели?
5. Два стрелка одновременно сделали по одному выстрелу в мишень. Вероятность попадания для первого стрелка 0,7, а для второго 0,6. Найти вероятность того, что в мишень попал один стрелок.
6. Три студента сдают экзамен. Вероятность получить положительную оценку для первого студента равна 0,8, для второго – 0,9, для третьего – 0,6. Какова вероятность того, что экзамен будет сдан только одним из студентов?
7. Найти вероятность того, что при трех подбрасываниях игральной кости 6 очков выпадет два раза.
8. Вероятность получения отличной оценки на экзамене равна 1/7. Составить закон распределения случайной величины X - числа отличных оценок у четырех друзей. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение.
9. В урне лежат 8 синих и 4 красных шара. Один за другим из урны вынимают три шара. Составить закон распределения случайной величины X – числа синих шаров в выборке. Найти математическое ожидание случайной величины X.
10. Случайная величина X равномерно распределена в интервале (2;14). Найти: а) дифференциальную функцию случайной величины X; б) интегральную функцию; в) вероятность попадания случайной величины в интервал (11;13); г) математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X.
11. Нормально распределенная случайная величина X задана дифференциальной функцией f(x). Определить вероятность попадания случайной величины в интервал (2; 9).
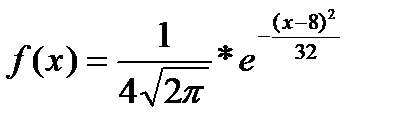
ВАРИАНТ 4.
1. Брошены две игральные кости. Сколько всего исходов имеет данный опыт? Найти вероятность того, что сумма очков на костях равна девяти.
2. Из букв разрезной азбуки составлено слово АТАКА. Ребенок, не умеющий читать, рассыпал эти буквы, а затем собрал их в произвольном порядке. Найти вероятность того, что у него получится исходное слово.
3. В «черном» ящике лежат 15 одинаковых на ощупь шаров, 8 из них – белые, остальные – красные. Найти вероятность того, что последовательно вынутые четыре шара окажутся красными.
4. В магазине имеется 20 пар обуви одной модели, из них 10 пар 39 размера. Найти вероятность того, что трем покупателям подряд понадобится именно 39 размер данной модели?
5. Два стрелка одновременно сделали по одному выстрелу в мишень. Вероятность попадания для первого стрелка 0,7, а для второго 0,6. Найти вероятность того, что в мишень попал хотя бы один стрелок.
6. Три студента сдают экзамен. Вероятность получить положительную оценку для первого студента равна 0,8, для второго – 0,9, для третьего – 0,6. Какова вероятность того, что экзамен будет сдан двумя студентами?
7. Найти вероятность того, что при восьми подбрасываниях монеты решка появится четыре раза.
8. Вероятность работы каждой из четырех швейных машин в мастерской без поломок в течение месяца равна 0,9. Составить закон распределения случайной величины X - числа швейных машин, работавших без поломок. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X.
9. В группе из 11 спортсменов 6 мастеров спорта. Составить закон распределения случайной величины X - числа мастеров спорта из трех случайным образом отобранных спортсменов. Найти математическое ожидание случайной величины X.
10. Случайная величина X равномерно распределена в интервале (-3;6). Найти: а) дифференциальную функцию случайной величины X; б) интегральную функцию; в) вероятность попадания случайной величины в интервал (-2;3); г) математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X.
11. Случайная величина распределена по нормальному закону с математическим ожиданием а = 25 и средним квадратическим отклонением σ=4. Определить вероятность попадания случайной величины в интервал (13; 35).
ВАРИАНТ 5.
1. Брошены две игральные кости. Сколько всего исходов имеет данный опыт? Найти вероятность того, что сумма очков на костях делится на три.
2. Из букв разрезной азбуки составлено слово МАШИНА. Ребенок, не умеющий читать, рассыпал эти буквы, а затем собрал их в произвольном порядке. Найти вероятность того, что у него получится исходное слово.
3. В «черном» ящике лежат 15 одинаковых на ощупь шаров, 8 из них – белые, остальные – красные. Найти вероятность того, что последовательно вынутые четыре шара окажутся белыми.
4. В магазине имеется 20 пар обуви одной модели, из них 8 пар 42 размера. Найти вероятность того, что четырем покупателям подряд понадобится именно 42 размер данной модели?
5. Два стрелка одновременно сделали по одному выстрелу в мишень. Вероятность попадания для первого стрелка 0,9, а для второго 0,4. Найти вероятность того, что в мишень попал один стрелок.
6. Три студента сдают экзамен. Вероятность получить положительную оценку для первого студента равна 0,5, для второго – 0,7, для третьего – 0,6. Какова вероятность того, что экзамен будет сдан только одним из студентов?
7. Найти вероятность того, что при четырех подбрасываниях игральной кости 6 очков выпадет три раза.
8. Вероятность рождения девочки равна 0,56. Составить закон распределения случайной величины X - числа девочек в семьях, имеющих четырех детей. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение.
9. В урне лежат 6 синих и 5 красных шаров. Один за другим из урны вынимают три шара. Составить закон распределения случайной величины X – числа красных шаров в выборке. Найти математическое ожидание случайной величины X.
10. Случайная величина X равномерно распределена в интервале (1;7). Найти: а) дифференциальную функцию случайной величины X; б) интегральную функцию; в) вероятность попадания случайной величины в интервал (1,5;3); г) математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X.
11. Нормально распределенная случайная величина X задана дифференциальной функцией f(x). Определить вероятность попадания случайной величины в интервал (3; 9).

ВАРИАНТ 6.
1. Брошены две игральные кости. Сколько всего исходов имеет данный опыт? Найти вероятность того, что сумма выпавших очков больше их произведения.
2. Из букв разрезной азбуки составлено слово СУММА. Ребенок, не умеющий читать, рассыпал эти буквы, а затем собрал их в произвольном порядке. Найти вероятность того, что у него получится исходное слово.
3. В «черном» ящике лежат 15 одинаковых на ощупь шаров, 8 из них – белые, остальные – красные. Найти вероятность того, что последовательно вынутые три шара окажутся красными.
4. В магазине имеется 20 пар обуви одной модели, из них 8 пар 37 размера. Найти вероятность того, что трем покупателям подряд понадобится именно 37 размер данной модели?
5. Два стрелка одновременно сделали по одному выстрелу в мишень. Вероятность попадания для первого стрелка 0,9, а для второго 0,4. Найти вероятность того, что в мишень попал хотя бы один стрелок.
6. Три студента сдают экзамен. Вероятность получить положительную оценку для первого студента равна 0,5, для второго – 0,7, для третьего – 0,6. Какова вероятность того, что экзамен будет сдан двумя студентами?
7. Найти вероятность того, что при восьми подбрасываниях монеты решка появится пять раз.
8. Вероятность получения отличной оценки на экзамене равна 2/9. Составить закон распределения случайной величины X - числа отличных оценок у четырех друзей. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение.
9. В группе из 11 спортсменов 5 мастеров спорта. Составить закон распределения случайной величины X - числа мастеров спорта из трех случайным образом отобранных спортсменов. Найти математическое ожидание случайной величины X.
10. Случайная величина X равномерно распределена в интервале (-3;7). Найти: а) дифференциальную функцию случайной величины X; б) интегральную функцию; в) вероятность попадания случайной величины в интервал (-2;4); г) математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X.
11. Вес карпов в пруду подчиняется нормальному закону распределения со средним квадратическим отклонением 120 г и математическим ожиданием 1000 г. Найти вероятность того, что вес пойманного карпа будет от 800 до 1300 г.
ВАРИАНТ 7.
1. Брошены две игральные кости. Сколько всего исходов имеет данный опыт? Найти вероятность того, что на обеих костях появится одинаковое число очков.
2. Из букв разрезной азбуки составлено слово ЯБЛОКО. Ребенок, не умеющий читать, рассыпал эти буквы, а затем собрал их в произвольном порядке. Найти вероятность того, что у него получится исходное слово.
3. В «черном» ящике лежат 15 одинаковых на ощупь шаров, 8 из них – белые, остальные – красные. Найти вероятность того, что последовательно вынутые три шара окажутся белыми.
4. В магазине имеется 20 пар обуви одной модели, из них 9 пар 36 размера. Найти вероятность того, что трем покупателям подряд понадобится именно 36 размер данной модели?
5. Два стрелка одновременно сделали по одному выстрелу в мишень. Вероятность попадания для первого стрелка 0,7, а для второго 0,4. Найти вероятность того, что в мишень попал один стрелок.
6. Три студента сдают экзамен. Вероятность получить положительную оценку для первого студента равна 0,9, для второго – 0,3, для третьего – 0,6. Какова вероятность того, что экзамен будет сдан только одним из студентов?
7. Найти вероятность того, что при пяти подбрасываниях игральной кости 6 очков выпадет два раза.
8. Вероятность работы каждой из четырех снегоуборочных машин без поломок в течение месяца равна 0,7. Составить закон распределения случайной величины X - числа снегоуборочных машин, работавших без поломок. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X.
9. В урне лежат 7 синих и 4 красных шаров. Один за другим из урны вынимают три шара. Составить закон распределения случайной величины X – числа синих шаров в выборке. Найти математическое ожидание случайной величины X.
10. Случайная величина X равномерно распределена в интервале (5;12). Найти: а) дифференциальную функцию случайной величины X; б) интегральную функцию; в) вероятность попадания случайной величины в интервал (6;10); г) математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X.
11. Нормально распределенная случайная величина X задана дифференциальной функцией f(x). Определить вероятность попадания случайной величины в интервал (0; 12).
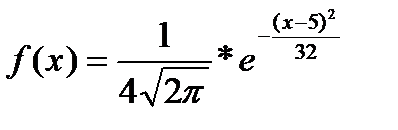
ВАРИАНТ 8.
1. Брошены две игральные кости. Сколько всего исходов имеет данный опыт? Найти вероятность того, что сумма выпавших очков не больше шести.
2. Из букв разрезной азбуки составлено слово БАНАН. Ребенок, не умеющий читать, рассыпал эти буквы, а затем собрал их в произвольном порядке. Найти вероятность того, что у него получится исходное слово.
3. В «черном» ящике лежат 15 одинаковых на ощупь шаров, 9 из них – белые, остальные – красные. Найти вероятность того, что последовательно вынутые четыре шара окажутся белыми.
4. В магазине имеется 20 пар обуви одной модели, из них 9 пар 41 размера. Найти вероятность того, что четырем покупателям подряд понадобится именно 41 размер данной модели?
5. Два стрелка одновременно сделали по одному выстрелу в мишень. Вероятность попадания для первого стрелка 0,7, а для второго 0,4. Найти вероятность того, что в мишень попал хотя бы один стрелок.
6. Три студента сдают экзамен. Вероятность получить положительную оценку для первого студента равна 0,9, для второго – 0,3, для третьего – 0,6. Какова вероятность того, что экзамен будет сдан двумя студентами?
7. Найти вероятность того, что при 12 подбрасываниях монеты решка появится три раза.
8. Вероятность рождения мальчика равна 0,55. Составить закон распределения случайной величины X - числа мальчиков в семьях, имеющих четырех детей. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение.
9. В группе из 11 спортсменов 4 мастера спорта. Составить закон распределения случайной величины X - числа мастеров спорта из трех случайным образом отобранных спортсменов. Найти математическое ожидание случайной величины X.
10. Случайная величина X равномерно распределена в интервале (-4;5). Найти: а) дифференциальную функцию случайной величины X; б) интегральную функцию; в) вероятность попадания случайной величины в интервал (-1;4); г) математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X.
11. Случайная величина распределена по нормальному закону с математическим ожиданием а = 30 и средним квадратическим отклонением σ=6. Определить вероятность попадания случайной величины в интервал (35; 47).
ВАРИАНТ 9.
1. Брошены две игральные кости. Сколько всего исходов имеет данный опыт? Найти вероятность того, что произведение выпавших очков равно 12.
2. Из букв разрезной азбуки составлено слово УРАГАН. Ребенок, не умеющий читать, рассыпал эти буквы, а затем собрал их в произвольном порядке. Найти вероятность того, что у него получится исходное слово.
3. В «черном» ящике лежат 15 одинаковых на ощупь шаров, 9 из них – белые, остальные – красные. Найти вероятность того, что последовательно вынутые четыре шара окажутся красными.
4. В магазине имеется 20 пар обуви одной модели, из них 12 пар 40 размера. Найти вероятность того, что трем покупателям подряд понадобится именно 40 размер данной модели?
5. Два стрелка одновременно сделали по одному выстрелу в мишень. Вероятность попадания для первого стрелка 0,8, а для второго 0,7. Найти вероятность того, что в мишень попал один стрелок.
6. Три студента сдают экзамен. Вероятность получить положительную оценку для первого студента равна 0,8, для второго – 0,7, для третьего – 0,6. Какова вероятность того, что экзамен будет сдан только одним из студентов?
7. Найти вероятность того, что при пяти подбрасываниях игральной кости 6 очков выпадет три раза.
8. Вероятность получения отличной оценки на экзамене равна 1/5. Составить закон распределения случайной величины X - числа отличных оценок у четырех друзей. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение.
9. В урне лежат 7 синих и 5 красных шаров. Один за другим из урны вынимают три шара. Составить закон распределения случайной величины X – числа красных шаров в выборке. Найти математическое ожидание случайной величины X.
10. Случайная величина X равномерно распределена в интервале (5;14). Найти: а) дифференциальную функцию случайной величины X; б) интегральную функцию; в) вероятность попадания случайной величины в интервал (6;13); г) математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X.
11. Нормально распределенная случайная величина X задана дифференциальной функцией f(x). Определить вероятность попадания случайной величины в интервал (3; 9).
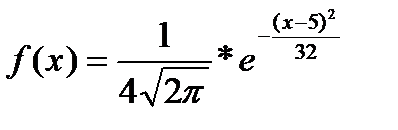
ВАРИАНТ 10.
1. Брошены две игральные кости. Сколько всего исходов имеет данный опыт? Найти вероятность того, что произведение выпавших очков не меньше 12.
2. Из букв разрезной азбуки составлено слово ПАПА. Ребенок, не умеющий читать, рассыпал эти буквы, а затем собрал их в произвольном порядке. Найти вероятность того, что у него получится исходное слово.
3. В «черном» ящике лежат 15 одинаковых на ощупь шаров, 9 из них – белые, остальные – красные. Найти вероятность того, что последовательно вынутые три шара окажутся белыми.
4. В магазине имеется 20 пар обуви одной модели, из них 12 пар 43 размера. Найти вероятность того, что четырем покупателям подряд понадобится именно 43 размер данной модели?
5. Два стрелка одновременно сделали по одному выстрелу в мишень. Вероятность попадания для первого стрелка 0,8, а для второго 0,7. Найти вероятность того, что в мишень попал хотя бы один стрелок.
6. Три студента сдают экзамен. Вероятность получить положительную оценку для первого студента равна 0,8, для второго – 0,7, для третьего – 0,6. Какова вероятность того, что экзамен будет сдан двумя студентами?
7. Найти вероятность того, что при 12 подбрасываниях монеты решка появится четыре раза.
8. Вероятность получения отличной оценки на экзамене равна 1/6. Составить закон распределения случайной величины X - числа отличных оценок у четырех друзей. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение.
9. В группе из 10 спортсменов 4 мастера спорта. Составить закон распределения случайной величины X - числа мастеров спорта из трех случайным образом отобранных спортсменов. Найти математическое ожидание случайной величины X.
10. Случайная величина X равномерно распределена в интервале (-2;7). Найти: а) дифференциальную функцию случайной величины X; б) интегральную функцию; в) вероятность попадания случайной величины в интервал (-1;3); г) математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X.
11. Вес карпов в пруду подчиняется нормальному закону распределения со средним квадратическим отклонением 150 г и математическим ожиданием 1000 г. Найти вероятность того, что вес пойманного карпа будет от 900 до 1300 г.
ПРИЛОЖЕНИЕ 6.1. Значения функции Пуассона: 
| l m. | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1.0 |
| 0.9048 0.0905 0.0045 0.0002 | 0.8187 0.1637 0.0164 0.0011 | 0.7408 0.2223 0.0ЗЗЗ 0.0033 | 0.6703 0.2681 0.0536 0.0072 | 0.6065 0.3033 0.0758 0.0126 | 0.5488 0.3293 0.0988 0.0198 | 0.4966 0.3476 0.1216 0.0284 | 0.4493 0.3595 0.1438 0.0383 | 0.4066 0.3659 0.1647 0.0494 | 0.3679 0.3679 0.1839 0.0613 | |
| 0.0001 | 0.0003 | 0.0007 | 0.0016 0.0002 | 0.003 0.0003 | 0.005 0.0007 0.0001 | 0.0077 0.0012 0.0002 | 0.0111 0.002 0.0003 | 0.0153 0.0031 0.0005 0.0001 |
| l m | |||||||||
| 0.1353 | 0.0498 | 0.0183 | 0.0067 | 0.0025 | 0.0009 | 0.0003 | 0.0001 | 0.0001 | |
| 0.2707 | 0.1494 | 0.0733 | 0.0337 | 0.0149 | 0.0064 | 0.0027 | 0.0011 | 0.0005 | |
| 0.2707 | 0.2240 | 0.1465 | 0.0842 | 0.0446 | 0.0223 | 0.0107 | 0.0050 | 0.0023 | |
| 0.1805 | 0.2240 | 0.1954 | 0.1404 | 0.0892 | 0.0521 | 0.0286 | 0.0150 | 0.0076 | |
| 0.0902 | 0.1681 | 0.1954 | 0.1755 | 0.1339 | 0.0912 | 0.0572 | 0.0337 | 0.0189 | |
| 0.0361 | 0.1008 | 0.1563 | 0.1755 | 0.1606 | 0.1277 | 0.0916 | 0.0607 | 0.0378 | |
| 0.0120 | 0.0504 | 0.1042 | 0.1462 | 0.1606 | 0.1490 | 0.1221 | 0.0911 | 0.0631 | |
| 0.0034 | 0.0216 | 0.0595 | 0.1045 | 0.1377 | 0.1490 | 0.1396 | 0.1171 | 0.0901 |
| 0.0009 | 0.0081 | 0.0298 | 0.0653 | 0.1033 | 0.1304 | 0.1396 | 0.1318 | 0.1126 | |
| 0.0002 | 0.0027 | 0.0132 | 0.0363 | 0.0689 | 0.1014 | 0.1241 | 0.1318 | 0.1251 | |
| 0.0008 | 0.0053 | 0.0181 | 0.0413 | 0.0710 . | 0.0993 | 0.1186 | 0.1251 | ||
| 0.0002 | 0.0019 | 0.0082 | 0.0225 | 0.0452 | 0.0722 | 0.0970 | 0.1137 | ||
| 0.0001 | 0.0006 | 0.0034 | 0.0113 | 0.0264 | 0.0481 | 0.0728 | 0.0948 | ||
| 0.0002 | 0.0013 | 0.0052 | 0.0142 | 0.0296 | 0.0504 | 0.0729 | |||
| 0.0001 | 0.0005 | 0.0022 | 0.0071 | 0.0169 | 0.0324 | 0.0521 | |||
| 0.0002 | 0.0009 | 0.0033 | 0.0090 | 0.0194 | 0.0347 | ||||
| 0.0003 | 0.0015 | 0.0045 | 0.0109 | 0.0217 | |||||
| 0.0001 | 0.0006 | 0.0021 | 0.0058 | 0.0128 | |||||
| 0.0002 | 0.0009 | 0.0029 | 0.0071 | ||||||
| 0.0001 | 0.0004 | 0.0014 | 0.0037 | ||||||
| 0.0002 | 0.0006 | 0.0019 | |||||||
| 0.0001 | 0.0003 | 0.0009 | |||||||
| 0.0001 | 0.0004 |
Приложение 6.2. Значения функции 
| Целые и десят. доли ‘x’ | Сотые доли 'х' | |||||||||
| 0.1 0.2 0.3 0.4 0.5 | 0.3989 0.3970 0.3910 0.3814 0.3683 0.3521 | 0.3989 0.3965 0.3902 0.3802 0.3668 0.3503 | 0.3989 0.3961 0.3894 0.3790 0.3653 0.3485 | 0.3988 0.3956 0.3885 0.3778 0.3637 0.3467 | 0.3986 0.3951 0.3876 0.3765 0/3621 0.3448 | 0.3984 0.3945 0.3867 0.3752 0.3605 0.3429 | 0.3982 0.3939 0.3857 0.3739 0.3589 0.3410 | 0.3980 0.3932 0.3847 0.3726 0.3572 0.3391 | 0.3977 0.3925 0.3836 0.3712 0.3555 0.3372 | 0.3973 0.3918 0.3825 0.3697 0.3538 0.3352 |
| 0.6 0.7 0.8 0.9 1.0 | 0.3332 0.3123 0.2897 0.2661 0.2420 | 0.3312 0.3101 0.2874 0.2637 0.2396 | 0.3292 0.3079 0.2850 0.2613 0.2371 | 0.3271 0.3056 0.2827 0.2589 0.2347 | 0.3251 0,3034 0.2803 0.2565 0.2323 | 0.2780 0.2541 0.2299 | 0.3209 0.2989 0.2756 0.2516 0.2275 | 0.3187 0.2966 0.2732 0.2492 0.2251 | 0.3166 0.2943 0.2709 0.2468 0.2227 | 0.3144 0.2920 0.2685 0.2444 0.2203 |
| 1.1 1.2 1.3 1.4 1.5 | 0.2179 0.1942 0.1714 0.1497 0.1295 | 0.2155 0.1919 0.1691 0.1476 0.1276 | 0.2131 0.1895 0.1669 0.1456 0.1257 | 0.2107 0.1872 0.1647 0.1435 0.1238 | 0.2083 0.1849 0.1626 0.1415 0.1219 | 0.2059 0.1826 0.1604 0.1394 0.1200 | 0.2036 0.1804 0.1582 0.1374 0.1182 | 0.2012 0.1781 0.1561 0.1354 0.1163 | 0.1989 0.1758 0.1539 0.1334 0.1145 | 0.1965 0.1736 0.1518 0.1315 0.1127 |
| 1.6 1.7 1.8 1.9 2.0 | 0.1109 0.0940 0.0790 0.0656 0.0540 | 0.1092 0.0925 0.0775 0.0644 0.0529 | 0.1074 0.0909 0.0761 0.0632 0.0519 | 0.1057 0.0893 0.0748 0.0620 0.0508 | 0.1040 0.0878 0.0734 0.0608 0.0498 | 0.1023 0.0863 0.0721 0.0596 0.0488 | 0.1006 0.0848 0.0707 0.0584 0.0478 | 0.0989 0.0833 0.0694 0.0573 0.0468 | 0.0973 0.0818 0.0681 0.0562 0.0459 | 0.0957 0.0804 0.0669 0.0551 0.0449 |
| Целые и десят. доли ‘x’ | Сотые доли ‘x’ | |||||||||
| 2.1 | 0.0440 | 0.0431 | 0.0422 | 0.0413 | 0.0404 | 0.0396 | 0.0387 | 0.0379 | 0.0371 | 0.0363 |
| 2.2 | 0.0355 | 0.0347 | 0.0339 | 0,0332 | 0.0325 | 0.0317 | 0.0310 | 0.0303 | 0.0297 | 0.0290 |
| 2.3 | 0.0283 | 0.0277 | 0.0270 | 0.0264 | 0.0258 | 0.0252 | 0.0246 | 0.0241 | 0.0235 | 0.0229 |
| 2.4 | 0.0224 | 0.0219 | 0.0213 | 0.0208 | 0.0203 | 0.0198 | 0.0194 | 0.0189 | 0.0184 | 0.0180 |
| 2.5 | 0.0175 | 0.0171 | 0.0167 | 0.0163 | 0.0158 | 0.0154 | 0.0151 | 0.0147 | 0.0143 | 0.0139 |
| 2.6 | 0.0136 | 0.0132 | 0.0129 | 0.0126 | 0.0122 | 0.0119 | 0.0116 | 0.0113 | 0.0110 | 0.0107 |
| 2.7 | 0.0104 | 0.0101 | 0.0099 | 0.0096 | 0.0093 | 0.0091 | 0.0088 | 0.0086 | 0.0084 | 0.0081 |
| 2.8 | 0.0079 | 0.0077 | 0.0075 | 0.0073 | 0.0071 | 0.0069 | 0.0067 | 0.0065 | 0.0063 | 0.0061 |
| 2.9 | 0.0060 | 0.0058 | 0.0056 | 0.0055 | 0.0053 | 0.0051 | 0.0050 | 0.0048 | 0.0047 | 0.0046 |
| 3.0 | 0.0044 | 0.0043 | 0.0042 | 0.0041 | 0.0039 | 0.0038 | 0.0037 | 0.0036 | 0.0035 | 0.0034 |
| 3.1 | 0.0033 | 0.0032 | 0.0031 | 0.0030 | 0.0029 | 0.0028 | 0.0027 | 0.0026 | 0.0025 | 0.0025 |
| 3.2 | 0.0024 | 0.0021 | 0.0022 | 0.0022 | 0.0021 | 0.0020 | 0.0020 | 0.0019 | 0.0018 | 0.0018 |
| 3.3 | 0.0017 | 0.0017 | 0.0016 | 0.0016 | 0.0015 | 0.0015 | 0.0014 | 0.0014 | 0.0013 | 0.0013 |
| 3.4 | 0.0012 | 0.0012 | 0.0012 | 0.0011 | 0.0011 | 0.0010 | 0.0010 | 0.0010 | 0.0009 | 0.0009 |
| 3.5 | 0.0009 | 0.0008 | 0.0008 | 0.0008 | 0.0008 | 0.0007 | 0.0007 | 0.0007 | 0.0007 | 0.0006 |
| 3.6 | 0.0006 | 0.0006 | 0.0006 | 0.0005 | 0.0005 | 0.0005 | 0.0005 | 0.0005 | 0.0005 | 0.0004 |
| 3.7 | 0.0004 | 0.0004 | 0.0004 | 0.0004 | 0.0004 | 0.0004 | 0.0003 | 0.0003 | 0.0003 | 0.0003 |
| 3.8 | 0.0003 | 0.0003 | 0.0003 | 0.0003 | 0.0003 | 0.0002 | 0.0602 | 0.0002 | 0.0002 | 0.0002 |
| 3.9 | 0.0002 | 0.0002 | 0.0002 | 0.0002 | 0.0002 | 0.0002 | 0.0002 | 0.0002 | 0,0001 | 0.0001 |
| 4.0 | 0.0001 | 0.0001 | 0.0001 | 0.0001 | 0.0001 | 0.0001 | 0.0001 | 0.0001 | 0.0001 | 0.0001 |
ПРИЛОЖЕНИЕ 6.3. Значения функции