НЕПРЕРЫВНАЯ СЛУЧАЙНАЯ ВЕЛИЧИНА.

 

Непрерывной случайной величиной называется случайная величина, все возможные значения которой целиком заполняют некоторый промежуток на числовой прямой.

Функция распределения непрерывной случайной величины: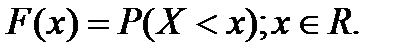

Функция не убывает и непрерывна, причем производная функции не имеет разрывов на всей числовой оси, за исключением конечного числа точек.

F(-¥)=0; F(+¥)=1.

Вероятность попадания случайной величины Х в интервал a£X<b определяется по формуле: P(a£X<b)=F(b)-F(a).

Плотность вероятности непрерывной случайной величины: f(x)=F’(x); xÎR.

Свойства плотности вероятности:

1. f(x)³0; xÎR.

2.

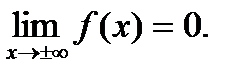
3.

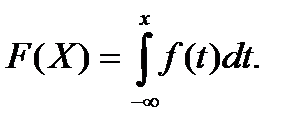
4. P(a£X<b)=F(b)-F(a)=

5.

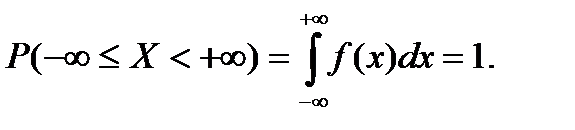
6. Математическое ожидание непрерывной случайной величины:

7. Дисперсия непрерывной случайной величины:

 

Нормальный закон распределения случайной величины.

Плотность вероятности: 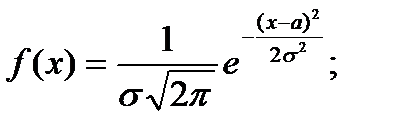xÎR.

Параметры нормального закона:

- математическое ожидание,

- среднее квадратическое отклонение.

Интегральная функция:

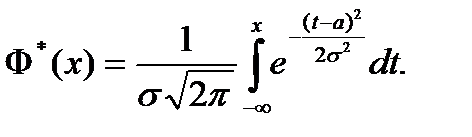
Свойства интегральной функции нормального закона:

1. F*(-¥)=0; F*(+¥)=1.

2. F*(x)=0,5+F(x), где F(x) – функция Лапласа.

3. F*(-x)=1-F*(x).

4.

5.

Сумма конечного числа независимых величин с нормальным законом распределения имеет нормальный закон распределения.

Важное применение для решения задач имеет теорема Ляпунова,согласно которой сумма большого количества независимых случайных непрерывных величин распределена по нормальному закону.

 

Равномерный закон распределения случайной величины.

Непрерывная случайная величина Х называется равномерно распределенной в интервале (a;b), если ее плотность распределения в этом интервале постоянна:

Интегральная функция:

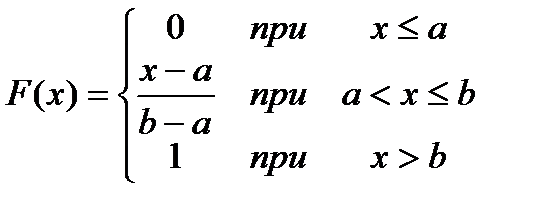
Вероятность попадания в заданный интервал (a;b):

Математическое ожидание:

Дисперсия:

Среднее квадратическое отклонение:

Показательный закон распределения случайной величины.

Плотность вероятности:

Параметр показательного закона: l - в теории массового обслуживания – среднее число событий, приходящихся на единицу времени.

Интегральная функция:

Вероятность попадания случайной величины в заданный интервал (a;b):

Математическое ожидание:

Дисперсия: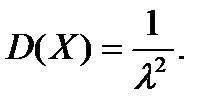

Среднее квадратическое отклонение:

При определенных условиях число событий, произошедших за промежуток времени t, распределено по закону Пуассона с математическим ожиданием а=lt. Длина промежутка t, между произвольными двумя соседними событиями, подчиняется показательному закону: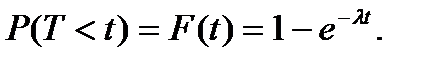

 

Пример 4.1. Дана плотность вероятности случайной величины X:

[ 0 , x£l

[ f(X)= 0,25 , 1<х£5. Найти функцию распределения, М(Х), D(X).

[ 0 , х>5

Решение. По определению функция распределения F(x)=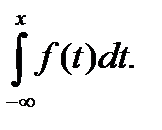

Следовательно, функция распределения принимает вид:

 

 

		x£1
F(X)=		1<х£5
		х>5

 

Математическое ожидание случайной величины:

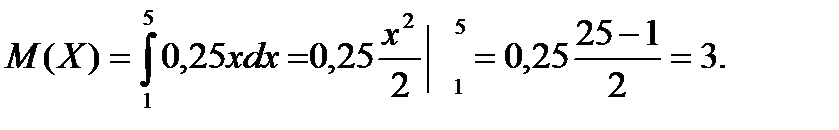
Дисперсия случайной величины:

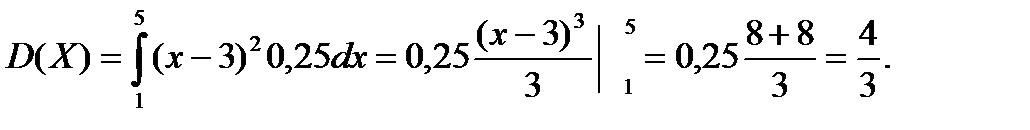
Пример 4.2. Торговая точка имеет в продаже большое количество различных товаров. Средняя выручка в день составляет 5 д.е., а среднее квадратическое отклонение 0,9 д.е. Составить плотность вероятности и функцию распределения выручки торговой точки. Найти вероятность того, что выручка торговой точки в случайно выбранный день: а) составит от 4 до 7 д.е., б) будет отличаться от средней выручки не более чем на 2 д.е.

Решение. X - выручка торговой точки, случайная величина, представляющая собой сумму большого количества случайных величин - выручек от продажи различных товаров, т.о., согласно теореме Ляпунова, имеет нормальный закон распределения.

Средняя выручка, по теории выборки (математическая статистика), является хорошей оценкой математического ожидания данной случайной величины. Следовательно: М(X)=5д.е.; s(Х)=0,9д.е.

Плотность вероятности - xÎR.

Функция распределения - xÎR.

Вероятность того, что выручка торговой точки составит от 4 до 7 д.е.:

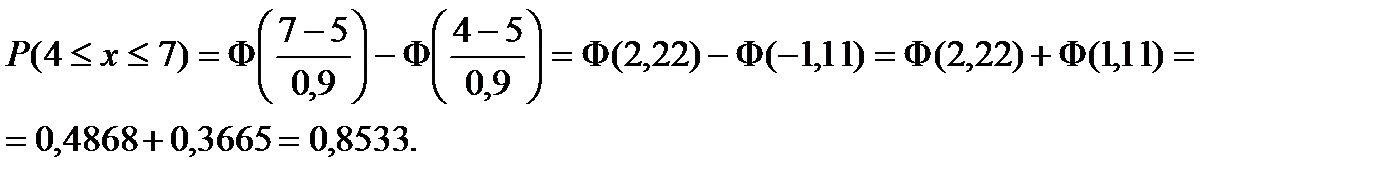
Вероятность того, что выручка будет отличаться от средней выручки не более чем на 2 д.е.:

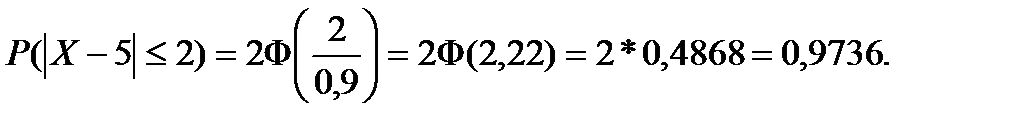
Пример 4.3. Автобусы некоторого маршрута идут строго по расписанию с интервалом движения 20 минут. Найти вероятность того, что пассажир, случайно подошедший к остановке, будет ожидать очередной автобус более 15 минут. Найти числовые характеристики полученной случайной величины.

Решение. Х- случайная величина, время ожидания пассажиром очередного автобуса. Случайная величина Х равномерно распределена в интервале (0;20].

a=0; b=20; a=15; b=20.

Плотность вероятности:

Вероятность ожидания автобуса более 15 минут:

Математическое ожидание:

Дисперсия: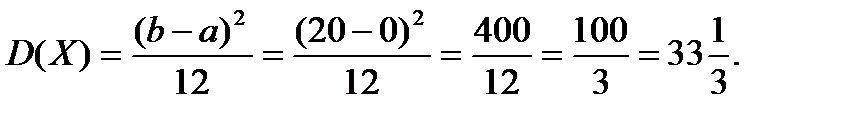

Среднее квадратическое отклонение:

 

Пример 4.4. Случайная величина Х – время безотказной работы прибора распределена по показательному закону с параметром l=0,01 1/час. Вышедший из строя прибор немедленно заменяют новым. Найти вероятность того, что неисправность прибора наступит не ранее, чем через 150 часов. Найти вероятность того, что за 200 часов прибор не придется заменять.

Решение. Случайная величина Х – время безотказной работы прибора распределена по показательному закону, следовательно:

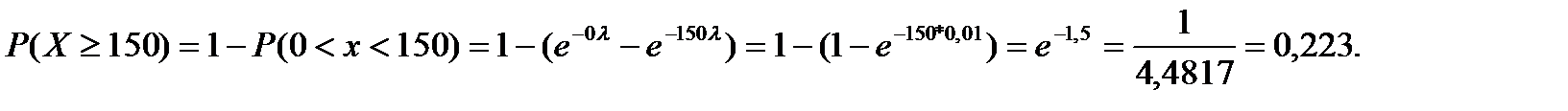
Число отказов прибора за время t=200 часов распределено по закону Пуассона с математическим ожиданием а=lt=0,01*200=2. Вероятность того, что за 200 часов прибор не придется заменять, вычисляется по формуле Пуассона: