Задания для текущего тестирования
1. Величины, адекватно характеризующие социально-экономические явления в конкретных условиях времени и места:
а) обобщающие показатели;
б) индивидуальные показатели;
в) статистические показатели.
2. Показатели, характеризующие размеры (объемы) изучаемых явлений:
а) относительные величины;
б) абсолютные величины;
в) обобщающие показатели.
3. Абсолютные величины - это:
а) показатели, характеризующие размер изучаемых явлений;
б) показатели, получаемые путем сравнения, сопоставления величин в пространстве, во времени или сравнение показателей разных свойств изучаемого объекта.
4. 10 рублей, 2 тонны, 1500 человеко-дней – это:
а) абсолютные величины; б) относительные величины.
5. 10 процентов, 0.2 промилле – это:
а) абсолютные величины; б) относительные величины.
6. Относительная величина структуры характеризует:
а) соотношение между частями статистической совокупности;
б) степень сравнения одноименных показателей в различных совокупностях;
в) развитие явления во времени;
г) удельный вес части изучаемого явления.
7. Относительная величина динамики характеризует:
а) соотношение между частями статистической совокупности;
б) степень сравнения одноименных показателей в различных совокупностях;
в) развитие явления во времени;
г) удельный вес части изучаемого явления.
8. Отношение одной части совокупности к другой части этой же совокупности – это относительная величина:
а) структуры; б) координации; в) сравнения.
9. Соотношение одного и того же абсолютного показателя, характеризующего разные объекты – это относительная величина:
а) структуры; б) координации; в) сравнения.
10. К условно-натуральным единицам измерения абсолютных статистических показателей можно отнести:
а. килограммы; б. человеко-часы; в. киловатт-часы. г. эталонные тракторы
11. Размер потребления различных видов продуктов на душу населения является частным случаем относительной величины:
а. сравнения б. динамики в. координации, г. интенсивности
12. Относительная величина уровня экономического развития является частным случаем относительной величины…
а. координации, б. интенсивности, в. динамики, г. сравнения
13. В статистике для расчета относительной величины интенсивности используются показатели, характеризующие:
а. явление; б. среду распространения явления;
в. динамику явлений; г. основные тенденции явлений
14. Взаимосвязь относительных величин динамики ОВД, планового здания ОВПЗ и выполнение плана ОВВП выражается соотношением:
а. ОВД = ОВПЗ : ОВВП, б. ОВД = ОВПЗ * ОВВП,
в. ОВВП = ОВД * ОВПЗ, г. ОВПЗ = ОВД * ОВВП
15. Для сравнения двух частей совокупности следует вычислить:
а. относительную величину координации,
б. относительную величину интенсивности,
в. индекс цен,
г. коэффициент пересчета
16. В теории статистики для расчета относительного показателя координации используются показатели, характеризующие…..:
а. часть совокупности, принятую за базу сравнения;
б. i-ю часть совокупности
17. Укажите относительные показатели, которые могут быть выражены именованными числами:
а. реализация плана, б. структуры,
в. интенсивности и уровня экономического развития, г. динамики
18. Средняя хронологическая применяется для вычисления среднего уровня моментного ряда динамики если:
а. между уровнями ряда динамики одинаковое расстояние,
б. между уровнями ряда динамики разное расстояние,
в. данные сопоставимы,
г. группировочный признак влияет на формирование системы показателей
19. Средний уровень моментного ряда при неравных интервалах между датами - средняя…
а. арифметическая простая,
б. геометрическая,
в. арифметическая взвешенная,
г. хронологическая взвешенная,
д. хронологическая простая
20. Значение средней арифметической взвешенной … при уменьшении всех частот в 2 раза
а. увеличится в 2 раза, б. увеличится в более чем в 2 раза,
в. не изменится, г. уменьшится более чем в 2 раза,
д. уменьшится в 2 раза
21. Если все частоты умножить на 25, то средняя:
а) не изменится; б) увеличится на 25; в) уменьшится в 25 раз.
22. Для расчета общей средней из групповых средних (удельный вес не одинаков) следует применить:
а. гармоническую взвешенную, б. гармоническую простую,
в. арифметическую простую, г. арифметическую взвешенную
23. 
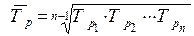- это формула средней:
а) квадратической; б) геометрической; в) хронологической.
24. 
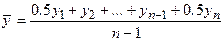- это формула средней:
а) квадратической; б) геометрической; в) хронологической.