Программа

Понятие о статистическом показателе, значение и функции статистических показателей. Классификация показателей. Система показателей. Абсолютные величины как исходная форма статистических показателей, их значение и виды.

Относительные величины, область их применения. Виды относительных величин, способы расчета и формы выражения. Взаимосвязь абсолютных и относительных величин, необходимость их комплексного применения.

Средняя величина, ее сущность и значение. Метод средних как один из важнейших приемов научного обобщения. Взаимосвязь метода средних и метода группировок, особенности использования в экономическом анализе. Виды средних величин; способы расчета и условия применения различных видов средних; экономическая интерпретация. Применение метода средних в исследовании социальных и экономических явлений.

Третьим этапом в программе статистического исследования является расчет обобщающих показателей. Статистические показатели представляют собой количественную характеристику различных свойств социально-экономических явлений. Вместе с тем, статистические показатели характеризуют и качественную сторону изучаемого явления. Для получения общей статистической характеристики изучаемого явления необходимо применить систему статистических показателей. При формировании системы статистических показателей необходимо четко сформулировать виды и формы систем, значение и область применения показателей, определить функции, которые им надлежит выполнять.

Все статистические показатели по охвату единиц совокупности делятся на индивидуальные и сводные, по форме выражения - на абсолютные, относительные и средние. Индивидуальные показатели характеризуют отдельный объект или отдельную единицу совокупности. Сводные показатели характеризуют группу единиц статистической совокупности или всю совокупность в целом. Сводные показатели подразделяются, в свою очередь, на объемные и расчетные. Объемные показатели получаются путем сложения значений признака отдельных единиц совокупности. Расчетные показатели - это показатели, которые могут быть получены в результате вычислений по различным формулам. В эту группу показателей входят показатели центра распределения, показатели вариации, индексы, показатели рядов динамики и др.

При изучении статистических показателей различают состояние социально-экономических явлений на конкретный момент времени - моментные показатели и за определенный период - интервальные показатели.

Важное место в системе обобщающих показателей занимают абсолютные и относительные величины. Исходной, первичной формой выражения статистических показателей являются абсолютные величины.

Абсолютной величиной называются показатели, которые характеризуют абсолютные размеры изучаемых статистикой процессов и явлений: физические (длина, масса, площадь, объем) и общественные (стоимость).

Абсолютные величины, выражающие размеры явлений и процессов, получаются в результате статистического наблюдения и сводки исходной информации. Абсолютные величины широко используют в торговле, применяются в анализе и прогнозировании коммерческой деятельности, в экономике в целом. На их основе составляют хозяйственные договоры, оценивают объем спроса на конкретные товары, изделия.

Первоначальным видом статистических данных являются индивидуальные абсолютные величины. На основе индивидуальных абсолютных величин вычисляются обобщающие абсолютные величины, характеризующие изучаемую совокупность в целом или ее отдельные части. Абсолютные величины могут быть получены и в результате специальных расчетов. Абсолютные показатели всегда являются именованными числами. В зависимости от социально-экономической сущности изучаемых явлений они могут выражаться в натуральных, стоимостных или трудовых единицах измерения.

Натуральные единицы измерения применяются в тех случаях, когда единица измерения соответствует потребительским свойствам продукта. В международной практике используются такие натуральные единицы измерения, как тонны, килограммы, унции, метры, мили, километры, галлоны, литры, штуки и т.д. В группу натуральных входят также условно-натуральные единицы измерения, которые используются в тех случаях, когда какой-либо продукт имеет несколько разновидностей и общий объем можно определить только исходя из общего для всех разновидностей потребительского свойства (мясо, мясопродукты, молоко, молочные продукты и т.д.). Перевод в условные единицы осуществляется с помощью специальных коэффициентов, которые рассчитываются как отношение потребительских свойств отдельных разновидностей продукта к эталонному значению. Натуральные единицы могут быть и составными (сложными) - показатели грузооборота и пассажирооборота, показатели производства электроэнергии и т.д.

Стоимостными называются единицы измерения, которые дают денежную оценку социально-экономическим явлениям и процессам. К примеру, одним из важнейших стоимостных показателей в СНС, характеризующих общий уровень развития экономики страны, является валовой внутренний продукт (ВВП). К трудовым единицам измерения, которые учитывают как общие затраты труда на предприятии, так и трудоемкость отдельных операций технологического процесса, относятся человеко-дни и человеко-часы.

Несмотря на то, что абсолютные величины играют важную роль при анализе различных явлений, процессов, часто возникает необходимость различного рода сопоставлений. В соответствии с задачами исследования и направлениями сопоставления статистических данных применяются различные виды относительных величин: динамики, выполнения договорных обязательств, структуры, координации, сравнения, интенсивности.

Относительные величины представляют собой результат деления одного абсолютного показателя на другой и выражают соотношение между количественными характеристиками социально-экономических явлений и процессов. При расчете относительных величин абсолютный показатель, который находится в числителе отношения, называется текущим или сравниваемым; показатель, с которым производится сравнение называется основанием или базой сравнения. Относительные величины выражаются в коэффициентах, в процентах, в промилле.

Относительная величина динамики характеризует развитие изучаемого явления во времени и показывает во сколько раз изменился уровень показателя по сравнению с предшествующим (базисным) периодом. Обозначим: y_i – уровень показателя в текущем периоде, y_o - уровень показателя в базисном периоде. В этом случае относительная величина динамики (темп роста) может быть представлена в виде: ОВ_д= y_i:y_o.

Пример 1. Имеются следующие данные по предприятию. Рассчитать относительные величины динамики.

Показатель	На 1.01. 2005 г.	На 1.01. 2006 г.
Производственный капитал, в т.ч.
оборотные средства, из них
собственные средства
заемные средства

Используя данные таблицы, рассчитаем относительные величины динамики:

- по производственному капиталу – 46600 : 43750 * 100% = 106.51%

- по оборотным средствам – 5130 : 5680 * 100% = 90.32%

- по собственным средствам – 2565 : 3135 * 100% = 81.82%

- по заемным средствам – 2565 : 2545 * 100% = 100.79%

Относительные величины динамики показывают, что за анализируемый период производственный капитал предприятия вырос на 6.51%; в то же время оборотные средства уменьшились на 9.68%, собственные – на 18.18%, заемные средства увеличились на 0.79%.

Выбор базы сравнения зависит отцели исследования. Возможен расчет относительных величин динамики с постоянной и с переменной базой сравнения (относительная величина динамики определяется как отношение показателя y_i текущего периода к показателю y_i-1 предшествующего периода).

Относительная величина структуры представляет собой соотношение структурных частей изучаемого объекта и объекта в целом, т.е. характеризует удельный вес части изучаемого явления во всей совокупности. Пример 2. Воспользуемся данными примера 1 и рассчитаем относительные величины структуры.

Доля оборотных средств в общей стоимости производственного капитала предприятия составит:

- на 1 января 2005 г. – 5680 : 43750 * 100% = 12.98%

- на 1 января 2006 г. – 5130 : 46600 * 100% = 11.0%

Доля собственных в общей стоимости оборотных средств составит:

- на 1 января 2005 г. – 3135 : 5680 * 100% = 55.19%

- на 1 января 2006 г. – 2565 : 5130 * 100% = 50.0%

Из полученных показателей видно, что на предприятии доля оборотных средств в общей стоимости производственного капитала снизилась на 1.98% и на 1 января 2006 г. составила 11%. Доля собственных средств в общей стоимости оборотного капитала на 1.01.05 г. составила 55.19%, а на 1.01.06 г. снизилась и составила 50.0%, т.е. только на 50% необходимые предприятию запасы и затраты обеспечиваются собственными средствами.

Относительная величина, характеризующая соотношение между частями одного целого, называется относительной величиной координации.

Пример 3. Воспользуемся данными примера 1 и рассчитаем относительные величины координации.

Соотношение заемных и собственных средств предприятия составит:

- на 1.01 2005 г. – 2545 : 3135 = 0.8118 - на 1.01. 2006 г. – 2565 : 2565 = 1.0

Этот показатель говорит о том, что на каждый рубль собственных средств предприятия на 1 января 2005 г. приходилось 81.18 коп. заемных средств. А на 1 января 2006 г. – 1 руб.

Соотношение собственных и заемных средств составит:

- на 1.01 2005 г. – 3135 : 2545 = 1.2318 - на 1.01 2006 г. – 2565 : 2565 = 1.0

Этот показатель характеризует финансовую устойчивость или платежеспособность предприятия, т.е. его способность рассчитываться по своим обязательствам.

Пример 4. Исходные данные заданы в виде таблицы. Рассчитать относительные величины структуры и координации.

Структура экспорта РФ в I кв. 2005 г.

	млн. долл.	В % к max	в % к итогу
Экспорт всего в том числе: Оплата по контрактам (по договорам) по бартерным операциям в погашение государственного долга в кредит прочие расходы	9066.4 8063.3 496.7 372.2 108.7 25.5	6.16 4.62 1.35 0.32	88.9 5.5 4.1 1.2 0.3

На основе данных, приведенных в таблице, можем сделать вывод, что на каждый миллион долларов экспорта, оплаченного по контрактам, приходится 61.6 тысяч долларов бартерных операций; 46.2 тыс. долларов в погашение государственного долга; 13.5 тыс. долларов экспорта в кредит; 3.2 тыс. долларов экспорта по прочим расходам.

Пример 5. В штате магазина в отчетном периоде состояли 42 продавца и 7 фасовщиков. Относительная величина координации составляет: 42:7=6:1, т.е. на 6 продавцов приходится один фасовщик.

Относительной величиной интенсивности характеризует степень распространения изучаемого процесса или явленияи представляет собой отношение исследуемого показателя к показателю присущей ему среды. В их числе можно назвать показатели жизненного уровня населения, к которым относятся показатели потребления продуктов и товаров на душу населения, показатели обеспеченности населения жильем, автомобилями и т.д. Учитывая экономическую сущность относительной величины интенсивности, ее можно назвать показателем уровня экономического и социального развития.

Пример 6. В отчетном периоде розничный товарооборот области составил 3110.0 млн. руб., среднегодовая численность населения - 1680 тыс. чел. Показатель интенсивности развития товарооборота составил: 3110.0 : 1680 = 185.12 тыс. руб. на одного человека.

Относительная величина наглядности (сравнения) отражает результаты сопоставления одноименных показателей, относящихся к одному периоду времени, но к разным объектам или территориям.

Этот вид относительных величин применяется для сравнения уровня развития стран и регионов, для оценки результатов деятельности отдельных предприятий одной отрасли промышленности.

Пример 7. В отчетном периоде розничный товарооборот проданных товаров в городах составлял 518.0 млрд. руб., в сельских районах - 211.0 млрд. руб. Относительная величина сравнения - 518.0:211.0=2.5

Относительная величина выполнения договора характеризует уровень реально достигнутых результатов по сравнению с договорными обязательствами. Все субъекты финансово-хозяйственной сферы, начиная от небольших семейных предприятий и заканчивая крупными фирмами в той или иной степени осуществляют перспективное планирование своей деятельности, а также сравнивают реально достигнутые результаты с ранее намеченными. Для этой цели используются относительные величины плана (договора) и относительные величины реализации плана (договора).

Пример 8. Оборот коммерческой фирмы в 2005 г. составил 2500 млн. руб. Исходя из проведенного анализа, руководство фирмы считало реальным в следующем году довести оборот до 3200 млн. руб. Фактический оборот фирмы в 2006 г. составил 2800 млн. руб.

Рассчитаем относительные величины расчетного задания, выполнения расчетного задания и динамики; определим их взаимосвязь.

Относительная величина расчетного задания: 3200 : 2500 *100% = 128%

Относительная величина выполнения расчетного задания (выполнения договора): 2800 : 3200 *100% = 87.5%

Между относительными величинами расчетного задания, выполнения расчетного задания и динамики существует взаимосвязь:

ОВРз * ОВРвз = ОВД 1.28 * 0.875 = 1.12 или ОВД = 2800:2500 = 1.12

Пример 9. В годовом отчете городского департамента образования содержатся следующие данные по классам школ:

Показатели	Классы	Всего по департаменту

Число учеников на начало учебного года Поступило после начала учебного года, в т.ч. перешло из других школ города Число учеников на конец учебного года Число второгодников

На основе данных отчета определите по каждому классу и по департаменту города следующие показатели:

- число выбывших учеников за учебный год;

- показатель уровня выбытия (отсева) учащихся;

- количество успевающих учащихся;

- относительный показатель успеваемости;

- процент учащихся, оставленных на второй год.

Полученные результаты проанализируйте и сделайте выводы с учетом предполагаемых причин (версий).

Решение. На основе данных отчета определяем по каждому классу и по департаменту города число выбывших учеников за учебный год.

Для этого к числу учеников на начало учебного года добавить число учеников, поступивших в школу после начала учебного года, вычесть число учеников, перешедших из других школ города и вычесть число учеников на конец учебного года. (К примеру, для первого класса: 8400 + 320 – 240 – 8120 = 360.)

Показатель уровня выбытия (отсева) учащихся определяется по каждому классу и по департаменту путем деления полученного числа выбывших учеников за учебный год на численность учащихся на конец учебного года. (К примеру, для второго класса: 520 : 8240*100 % = 6.31%.)

Количество успевающих учащихся определяется по каждому классу и по департаменту путем вычитания количества второгодников из количества учащихся на конец года. (К примеру, для третьего класса: 8660 – 189 = 8471.)

Относительный показатель успеваемости учащихся определяется по каждому классу и по департаменту путем деления полученного числа успевающих учеников за учебный год на численность учащихся на конец учебного года. (К примеру, для четвертого класса: 7990 : 8200 × 100 % = 97.43 %.)

Процент учащихся, оставленных на второй год, определяется по каждому классу и по департаменту путем деления числа второгодников за учебный год на численность учащихся на конец учебного года. (К примеру для пятого класса: 100 % – 97.07 % = 2.93%). Все расчетные показатели представим в виде таблицы.

Показатели	Классы	Всего по департаменту

1. Число выбывших учеников за учебный год, чел. 2. Показатель уровня выбытия (отсева) учащихся, % 3. Количество успевающих учащихся, чел. 4. Относительный показатель успеваемости , % 5. Процент учащихся, оставленных на второй год, %	4.43 98.79 1.21	6.31 99.21 0.79	2.65 97.81 2.19	3.04 97.43 2.57	3.42 97.07 2.93	3.68 97.08 2.92	3.13 97.82 2.18

По данным таблицы можно сделать выводы:

Общее число выбывших учеников по департаменту составляет 2295 чел., а показатель отсева 3.13%. Наибольший процент выбывших учеников во втором классе (6.31%), а наименьший – в третьем (2.65%).

Общее количество успевающих учащихся по департаменту 71510 чел., в т.ч. в относительном выражении это составляет: наилучший показатель успеваемости – во втором классе (99.21%), наихудший – в пятом классе (97.07%). Из этого следует, что во втором классе наименьший процент учащихся, оставленных на второй год (0.79%), а в пятом – наибольший процент (2.93%).

Наиболее распространенной формой статистических показателей, используемых в социально-экономических исследованиях, является средняя величина. Средняя величина представляет собой обобщенную количественную характеристику признака в качественно однородной совокупности в конкретных условиях места и времени. Если совокупность неоднородна, то ее нужно разбить на однородные группы, для каждой из которых определяется средняя величина.

В зависимости от задач исследования в ряде случаев необходимо вычислить общие средние для совокупности, состоящей из нескольких неоднородных групп. Средние, вычисленные для каждой группы, называются групповыми средними. Общая средняя отражает общие черты изучаемого явления, групповая средняя дает характеристику размера явления.

Важное свойство средней величины заключается в том, что она отражает то общее, что присуще всем единицам исследуемой совокупности. Значения признака отдельных единиц совокупности могут колебаться в ту или иную сторону под влиянием множества факторов, среди которых могут быть как основные, так и случайные. Сущность средней в том и заключается, что в ней взаимно погашаются отклонения значений признака отдельных единиц совокупности, обусловленные действием случайных факторов и учитываются изменения, вызванные действием факторов основных. Это позволяет средней отражать типичный уровень признака и абстрагироваться от индивидуальных особенностей, присущих отдельным единицам. Типичность средней непосредственным образом связана с однородностью статистической совокупности. Средняя величина только тогда будет отражать типичный уровень признака, когда она рассчитана по качественно однородной совокупности.

Существуют две категории средних величин: степенные и структурные средние. Выбор того или иного вида средней происходит в зависимости от цели исследования, экономической сущности усредняемого показателя и характера имеющихся данных. Средние величины, как любое понятие - научная абстракция. Средней величине присущи и недостатки - в ней погашаются индивидуальные различия отдельных единиц изучаемой совокупности.

Прежде чем вычислить средние величины, необходимо исследовать состав совокупности, обеспечить качественную однородность единиц: нельзя ограничиться вычислением средней для всей совокупности, следует использовать групповые средние для отдельных ее частей; метод средних должен сочетаться с методом группировок.

Как отмечалось выше, в статистических исследованиях применяют различные виды степенных средних величин. Средняя арифметическая - наиболее часто употребляемый в статистических исследованиях вид средней. Средняя арифметическая бывает простая и взвешенная. Под взвешиванием в статистике понимается процесс умножения значений изучаемого признака (х) на соответствующие веса (f). Часто весами служат частоты - величины, показывающие, сколько раз встречается в данной совокупности каждое значение изучаемого признака.

Средняя арифметическая применяется, если известны значения признака х и число единиц f, обладающих этим признаком. Если для каждого х имеется только одна единица, обладающая данным признаком, применяется средняя арифметическая простая

Если в исходных данных известны значения признака х и для каждого признака своя численность единиц f, применяется средняя арифметическая взвешенная

Для расчета средней арифметической из интервального ряда необходимо выполнить следующие действия:

- закрыть открытые интервалы (если они есть), приняв их равными ближайшим закрытым;

- от интервального ряда перейти к дискретному, приняв за значение х середину интервалов;

- произвести расчет средней арифметической взвешенной.

Средняя гармоническая, как и средняя арифметическая бывает простой и взвешенной. Простая средняя гармоническая определяется по формуле

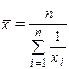
Средняя гармоническая взвешенная рассчитывается по формуле

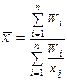W - объем признака, для которого находится средняя.

Если необходимо найти среднюю заработную плату, то W - фонд заработной платы; если находим средние затраты времени на изготовление одного станка, то W - общие затраты времени на изготовление; если находим среднюю урожайность, то W - урожай всего поля.

Иногда по исходным данным трудно определить какой вид средней выбрать. В этом случае необходимо написать логическую формулу расчета того показателя, для которого определяется средняя. Если в исходных данных задан числитель логической формулы, то для расчета средней применяется средняя гармоническая взвешенная. Если в исходных данных задан знаменатель логической формулы, то для расчета средней применяется средняя арифметическая взвешенная.

Пример. Исходные данные заданы в виде таблицы. Определить средний процент выполнения плана товарооборота двумя магазинами.

Магазины	Фактический товарооборот, млн.руб.	Выполнение плана, %
	198.0	90.0
	84.0	105.0

Процент выполнения плана - это относительная величина выполнения плана, которая равна отношению фактического товарооборота к плановому. Так как в исходных данных известен числитель логической формулы, то для определения среднего процента выполнения плана применяем формулу средней гармонической взвешенной.

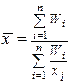= (198.0 + 84.0):(198.0:90.0 + 84.0:105.0) = 94.0.

Вывод: два магазина выполнили план товарооборота в среднем на 94 процента.

Пример. Исходные данные заданы в виде таблицы. Определить средний процент выполнения плана.

Магазины	Плановый товарооборот, млн.руб.	Выполнение плана, %
	400.0	105.0
	200.0	120.0

Поскольку в исходных данных задан знаменатель логической формулы относительной величины выполнения плана, то для нахождения среднего процента выполнения плана применяем формулу средней арифметической взвешенной.

= (400.0´105.0 + 200.0´120.0):(400.0 + 200.0) = 110.0.

Вывод: средний процент выполнения плана двумя магазинами равен 110%.

Пример. Исходные данные заданы в виде таблицы.

Фабрики	Фактический выпуск продукции за отчетный период, млн.руб.	Процент выполнения Плана	Процент стандартной продукции
	665.0
	880.0

Определить:

- средний процент выполнения плана двумя фабриками;

- средний процент стандартной продукции.

Для вычисления среднего процента выполнения плана применяем формулу средней гармонической взвешенной, т.к. в исходных данных известен числитель логической формулы относительной величины выполнения плана.

= (665.0 + 880.0):(665.0:95.0 + 880.0:110.0) = 103.0.

Для вычисления среднего процента стандартной продукции применяем формулу средней арифметической взвешенной, т.к. в исходных данных задан знаменатель логической формулы относительной величины структуры.

= (665.0 ´ 80.0 + 880.0 ´ 90.0):(665.0 + 880.0) = 85.7.

Вывод: средний процент выполнения плана двумя фабриками составляет 103%, средний процент стандартной продукции в общем объеме выпускаемой продукции составляет 85.7%.

Пример. Имеются данные о посевной площади и урожайности пшеницы:

№ бригады	2005 год	2006 год
Урожайность, ц/га	Площадь, ц/га	Урожайность, ц/га	Валовой, сбор, ц
	19.5		22.0
	20.0		23.5
	21.6		24.0

На основе приведенных данных:

- определить среднюю урожайность пшеницы по всем бригадам в 2005 и в 2006 годах;

- как изменилась урожайность в 2006 году по сравнению с 2005 годом;

- дайте обоснование применения соответствующих формул для расчета средних величин.

Для решения необходимо составить логическую формулу урожайности

,

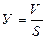где У - урожайность, ц/га, V - валовый сбор, ц, S - площадь, га.

В исходных данных за 2005 год задан знаменатель логической формулы (S), следовательно, для расчета средней урожайности пшеницы по всем бригадам необходимо использовать формулу средней арифметической взвешенной. В исходных данных за 2006 год задан числитель логической формулы (В), следовательно, для расчета средней урожайности пшеницы по всем бригадам необходимо использовать формулу средней гармонической.

Вычислим среднюю урожайность пшеницы по бригадам в 2005.

,

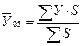где 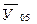- средняя урожайность пшеницы за 2005 год;

.

Получили, что средняя урожайность пшеницы в 2005 году по всем бригадам составила 20.3 ц/га. При вычислении средней урожайности пшеницы за 2006 год, как указывалось выше, используем формулу средней гармонической.

,

где 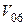- валовый сбор пшеницы за 2006 год по всем бригадам;

.

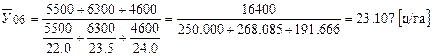Таким образом, средняя урожайность пшеницы в 2006 году по всем бригадам составила 23.1 ц/га.

Для того, чтобы определить как изменилась средняя урожайность пшеницы в 2006 г. по сравнению с 2005 г., в абсолютных и в относительных величинах, необходимо вычислить:

- абсолютный прирост : D 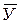= - 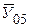=23.1 - 20.3 = 2.8 ц/га;

- темп роста : .

Средняя урожайность пшеницы в 2006 г. возросла по сравнению со средней урожайностью в 2005 г. в 1.14 раза (на 14%) или на 2.8 ц/га.

Средняя квадратическая (среднее квадратическое отклонение) применяется для расчета вариации (колеблемости) признаков. Среднее квадратическое отклонение - абсолютная мера вариации.

Среднее квадратическое отклонение взвешенное имеет вид:

.

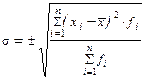Среднее квадратическое отклонение простое имеет вид:

.

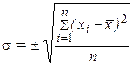Чем меньше среднее квадратическое отклонение, тем однороднее совокупность, тем типичнее средняя, тем устойчивее явление или процесс.

Средняя хронологическая (средний уровень ряда) применяется, когда известны значения признака на несколько дат внутри периода.

Средняя хронологическая применяется в рядах динамики для определения среднего уровня ряда.

,

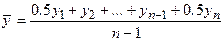где 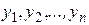- уровни ряда динамики; n - число уровней.

Средняя геометрическая применяется в рядах динамики для определения среднего темпа роста

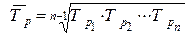, где 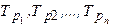- темпы роста.

Выбор вида средней в статистических исследованиях зависит от исходных данных. Для характеристики среднего значения признака в вариационном ряду, кроме средней арифметической, используются так называемые структурные средние - мода и медиана. В отличие от средней арифметической, рассчитываемой на базе всех вариантов значений признака, мода и медиана характеризуют величину варианты, занимающей определенное положение в ранжированном вариационном ряду.

Мода – чаще всего встречающееся в изучаемой совокупности, наиболее характерное для нее значение признака. Мода может характеризовать товары наибольшего спроса. В этом случае изучаемый признак – атрибутивный. Мода может характеризовать и наиболее ходовой размер обуви. В этом случае изучаемый признак – количественный.

Для дискретного ряда распределения мода определяется как значение признака (варианты) с наибольшей частотой. В интервальном ряду распределения с равными интервалами наибольшая частота указывает на модальный интервал. Моду для интервального ряда с равными интервалами можно определить по формуле:

,

где 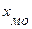– начальное значение интервала, содержащего моду;

h – величина интервала;

- частота модального интервала;

– частота интервала, предшествующего модальному;

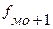– частота интервала, следующего за модальным.

Если интервалы неравные, то вместо частот рекомендуется использовать плотность распределения частот.

Медианой в статистике называется варианта, расположенная в середине вариационного ряда. Если ряд распределения дискретный и имеет нечетное число вариант, то медианой будет варианта, находящаяся в середине упорядоченного (ранжированного) ряда. Если упорядоченный ряд состоит из четного числа вариант, то медианой будет средняя арифметическая из двух вариант, расположенных в середине ряда.

Медиана, в отличие от моды, может быть вычислена для рядов распределения с равными и неравными интервалами, так как при определении медианы учитывается изменение частоты только в медианном интервале.

Медиана интервального вариационного ряда распределения определяется по формуле:

,

где 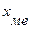– начальное значение медианного интервала;

h– величина интервала;

– сумма частот ряда;

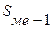– сумма накопленных частот, предшествующих медианному интервалу;

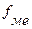– частота медианного интервала.

Медианный интервал – интервал, для которого первая накопительная частота больше (равна) полусуммы всех частот.

Соотношение моды, медианы и средней арифметической указывает на характер распределения признака в совокупности, позволяет оценить его асимметрию. В симметричных распределениях все три характеристики совпадают .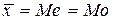

Лекция 4.При изучении данной темы особое внимание рекомендуется уделить классификации статистических показателей и принципам выбора конкретной их формы в зависимости от имеющихся данных и поставленной задачи. Статистические показатели представляют собой количественную характеристику различных свойств социально-экономических явлений. Вместе с тем, статистические показатели характеризуют и качественную сторону изучаемого явления. Все статистические показатели по охвату единиц совокупности делятся на индивидуальные и сводные, по форме выражения - на абсолютные, относительные и средние.При изучении статистических показателей различают состояние социально-экономических явлений на конкретный момент времени - моментные показатели и за определенный период - интервальные показатели.

Теоретическая основа, практические задачи, подробные методические рекомендации приводятся в литературе: обязательная - [2,7,10], 7 – стр.38 - 63, - дополнительная - [8, 9].

Для закрепления материала необходимо ответить на вопросы:

1. Охарактеризуйте третий этап статистического исследования.

2. Дайте характеристику обобщающих показателей. Как дифференцируются статистические показатели.

3. Что такое абсолютные показатели, их роль в статистическом исследовании, на практике.

4. Какие виды абсолютных величин вы знаете? Назовите единицы измерения абсолютных величин.

5. Дайте характеристику относительных величин; их роль и значение в исследованиях, на практике.

6. Почему необходимо использовать абсолютные и относительные показатели во взаимосвязи.

7. Что представляет собой средняя величина и в чем состоит ее определяющее свойство.

8. Дайте характеристику структурных средних. Изобразите графически структурные средние.

9. В чем различие между степенными и структурными средними.

10. Какие виды средних вы знаете. Экономическая интерпретация средних величин.

Практическое занятие 3. На практических занятиях по теме студенты должны усвоить смысл понятий абсолютных и относительных величин; методов расчета и графического изображения различных видов относительных величин; уметь выполнять компьютерный анализ по данной теме. Практические занятия по теме предусматривают решение задач на вычисление средних величин, показателей структуры распределения.