Нагрузки и воздействия на расчетные схемы

Все воздействия на сооружения можно разделить на силовые (нагрузки), температурные и кинематические (смещения опор и связей).

При этом воздействия могут быть статическими и динамическими.

К статическим относят воздействия и нагрузки, которые при приложении возрастают от нуля до конечной величины настолько медленно, что скорости
и ускорения точек систем при их деформировании малы и можно пренебречь силами инерции.

К динамическим относят воздействия, которые сообщают массам сооружения существенные ускорения и соответственно вызывают такие силы инерции, что их влияние должно учитываться.

Силовые воздействия или нагрузки представляются сосредоточенными
силами, сосредоточенными моментами, распределенными нагрузками постоянной или переменной интенсивности. Эти нагрузки могут быть подвижными
и неподвижными. Неподвижные нагрузки действуют постоянно в одном месте. Подвижные перемещаются по системе (например, транспорт по мосту).

5.- изгибающий момент М, действующий в плоскости сооружения относительно центральной оси поперечного сечения элемента (стержня), перпендикулярной к этой плоскости;

- поперечная силаQ, действующая в плоскости поперечного сечения
в направлении центральной оси поперечного сечения, лежащей в плоскости
сооружения;

- продольная силаN, действующая перпендикулярно к сечению (вдоль
оси стержня) и приложенная в центре тяжести сечения.

6.В заданном месте проводится сечение, разделяющее систему на две части. Затем рассматривается равновесие одной из частей системы. При этом действие отброшенной части на рассматриваемую заменяется силами, равными внутренним силам в сечении. Эти силы действуют на рассматриваемую часть как внешние силы. Из уравнений равновесия, число которых равно трем (что соответствует количеству неизвестных внутренних сил), определяются усилия в рассматриваемом сечении системы.

7. Изгибающий момент в сечении численно равен алгебраической сумме моментов всех внешних сил (включая и опорные реакции), приложенных к части системы с одной стороны от сечения, относительно центра тяжести сечения.

8. Поперечная сила в сечении численно равна алгебраической сумме проекций всех внешних сил (включая опорные реакции), приложенных к части системы с одной стороны от сечения, на ось, перпендикулярную к оси стержня.

9. Продольная сила в сечении численно равна алгебраической сумме проекций всех внешних сил (включая опорные реакции), приложенных к части системы с одной стороны от сечения, на ось, касательную к оси стержня (для прямолинейных стержней – на ось самого стержня).

10. Эпюрой усилия (M, Q, N и др.) называется график (диаграмма), отражающий зависимость изменения этого усилия по длинам всех элементов (стержней) системы от действия постоянной нагрузки.

11.Степень свободы системы – это число независимых геометрических параметров (перемещений, координат), определяющих положение всех элементов сооружения на плоскости или в пространстве.

Определение степени свободы системы может быть выполнено по формулам:

1. W = − (3K − Ш),

где: K – число замкнутых контуров в системе

Ш – число простых, одиночных шарниров в системе, включая шарниры между дисками (стержнями) и основанием (землей).

W = 3D −2Ш − C₀ ,

где: D – число дисков в системе;

Ш – число одиночных (простых) шарниров, соединяющих диски D;

С₀ – число кинематических опорных связей в системе.

Для ферм - W = 2У − С − С₀ ,

где: У – число шарнирных узлов в ферме; С – число стержней фермы;

С₀ – число опорных связей.

12.1) определение степени свободы системы;

2) геометрический анализ структуры системы (геометрически изменяема или

нет).

13.1.Три диска, соединенные друг с другом последовательно тремя шарнирами, не лежащими на одной прямой, образуют неизменяемую систему, то есть такая система в целом является диском

2. Если точка присоединяется к диску двумя стержнями, не лежащими на одной прямой, то такая система в целом неизменяема, т.е. является диском.

3. Два диска, соединенные друг с другом тремя стержнями, не параллельными друг другу и не пересекающимися в одной точке, образуют неизменяемую систему, то есть такая система в целом является диском

4. Три диска, соединенные последовательно друг с другом парами стержней, точки пересечения которых не лежат на одной прямой, образуют неизменяемую систему, и система в целом является диском.

 

18.Основным методом определения усилий в стержнях статически определимых ферм является метод сечений. Ферма сквозным или замкнутым сечением (рис. 3.25) разрезается (разделяется) на две или несколько частей так, чтобы был рассечен стержень, в котором определяется усилие. После этого рассматривается равновесие одной из частей, действие на которую отброшенной части (частей) фермы заменяется пока неизвестными продольными силами. Направляют эти продольные силы обычно от узлов (от сечений), что соответствует
положительным для них направлениям, при которых в стержнях возникает растяжение (рис. 3.25б). Из уравнений равновесия определяются искомые продольные силы и устанавливается истинный знак усилий (если усилие получилось отрицательным, значит оно будет направлено в противоположную сторону и в стержне будет иметь место сжатие). Метод сечений для ферм реализуется с помощью способов вырезания узлов, моментной точки и проекций.

24.При расчете статически неопределимых систем методом сил за неизвестные принимаются усилия в лишних связях, после определения которых легко находятся внутренние силы (M, Q, N) в сечениях системы и перемещения ее точек.

Но задача может быть решена и в обратном направлении. Если сначала
определить деформированный вид системы (перемещения точек), то затем можно установить и соответствующее им распределение внутренних сил, что иллюстрирует и широко известная зависимость

Именно такой подход и используется в методе перемещений. При этом анализ показывает, что деформированный вид системы полностью определен, если известны угловые и линейные перемещения ее узлов.

 

 

28.

1. Определяем степень статической неопределимости рамы (то есть число «лишних» связей в раме – Л), используя, например, формулы.

2. Выбираем расчетную основную систему метода сил (О.С.), представив предварительно несколько возможных вариантов основных систем.

3. Записываем в общем виде систему канонических уравнений метода сил и выясняем физический смысл этих уравнений и входящих в них величин.

4. В расчетной О.С. метода сил строим единичные 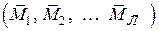и грузовую (М_Р) эпюры изгибающих моментов.

5. Вычисляем все единичные коэффициенты 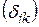и свободные члены системы канонических уравнений метода сил (4.6).

6. Выполняем проверки правильности вычисления единичных коэффициентов и свободных членов системы уравнений.

7. Решаем систему канонических уравнений и находим неизвестные метода сил Х₁, Х₂, … Х_Л ; выполняем проверку правильности решения системы уравнений, подставляя найденные неизвестные во все уравнения.

8. Строим в заданной статически неопределимой раме окончательную эпюру изгибающих моментов М (4.10).

9. Выполняем деформационную проверку эпюры М (см. 4.12 либо 4.11).

10. По эпюре М строим окончательную эпюру поперечных сил Q (используя зависимости 4.13 либо 4.14).

11. Способом вырезания узлов на эпюре Q с учетом действующих в узлах нагрузок строим в заданной раме эпюру продольных сил N.

12. Вырезая опорные узлы, определяем опорные реакции, и выполняем статическую проверку равновесия рамы в целом (4.15).

 

29. деформационная (кинематическая) проверка эпюры М; эта проверка здесь производится так же, как и методе сил; но здесь для ее выполнения вначале необходимо для заданной системы выбрать основную систа бы максимальное число участков системы; после этого
деформационная проверка выполняется по формуле:

или .

30. статическая проверка; выполняется так же, как и в методе сил, то есть вычисляются суммы проекций всех заданных нагрузок и опорных реакций на две любые оси и сумма моментов этих же сил и опорных реакций относительно любой точки, которые должны быть равны нулю.