Относительные величины

 

Анализируя статистические данные, необходимо сопоставлять явления во времени и пространстве, исследовать закономерности их изменения и развития, изучать структуру совокупностей. С помощью абсолютных величин эти задачи невыполнимы, в этом случае необходимо использовать относительные величины.

Относительная величина представляет собой результат сопоставления двух статистических показателей, дает цифровую меру их соотношения. В числителе дроби стоит величина, которую сравнивают, в знаменателе — величина, с которой сравнивают. Последняя называется базой(или основанием)сравнения.

В случае если основание принимается за 1, то относительная величина выражается как коэффициент (десятичная дробь), если за 100 - в процентах (%), если за 1000 — в промилле (⁰/₀₀), если за 10000 — в продецимилле (⁰/₀₀₀).

Выбор формы относительной величины зависит от ее абсолютного значения. Если сравниваемая величина больше базы сравнения в 2 раза и более, то обычно выбирают форму коэффициента, если относительная величина близка к единице, как правило, ее выражают в процентах, если число значительно меньше единицы, его рационально выразить в промилле.

Рассмотрим различные виды относительных величин.

Относительные величины структурыпоказывают удельный вес каждой группы в общем объеме совокупности. Их получают путем деления численности каждой группы, входящей в совокупность, на численность всей совокупности.

Пример. На 01.01.2010 г. в Томской области было 518,8 тыс. мужчин и 552,2 тыс. женщин. То есть всего население составляло 1071тыс. человек. Тогда относительная величина структуры составила:

- доля мужчин; - доля женщин. Сумма удельных весов всех групп всегда равна 100%.

Относительные величины структуры дают возможность сопоставлять структуры одной и той же совокупности в различные моменты времени. Такое сопоставление позволяет делать выводы о тенденциях и закономерностях структурных изменений во времени.

Относительные величины координацииполучают как соотношение между частями одного целого.

Пример. Соотношение числа мужчин и женщин в предыдущем примере: , то есть на одного мужчину приходилось 1,06 женщины.

Эти величины также могут быть использованы при вычислении отношения численности неработающих лиц к численности занятого населения, отношения стоимости импортных продуктов питания к стоимости отечественного продовольствия и др.

Относительные величины сравненияполучают в результате сопоставления одноименных абсолютных показателей, относящихся к разным совокупностям.

Пример. Цена на молоко в Томске составляет 26 рублей за литр, а в Новосибирске 28 рублей за литр, тогда относительная величина сравнения , то есть молоко в Новосибирске дороже, чем в Томске на 7,69%.

Эти величины могут быть использованы также при сравнении размера основных фондов пищевой промышленности двух регионов по состоянию на определенную дату или уровень потребления в расчете на душу населения жителями разных областей в третьем квартале текущего года и т.д. При определении относительных величин сравнения необходимо обеспечить единство методологииисчисления абсолютных показателей, подлежащих сопоставлению.

Относительные величины динамики— это результат сопоставления уровней одного и того же явления, относящихся к различным периодам или моментам времени. Они характеризуют степень изменения изучаемого явления во времени. Их называют коэффициентами роста. Коэффициент роста в процентах называют темпом роста, который может определяться с переменной или постоянной базой.

Темп роста с переменной базой получают при сравнении уровня явления каждого периода с уровнем предыдущего периода. Они называются цепными. Темпы роста с постоянной базой сравнения получают путем сопоставления уровня явления в каждом отдельном периоде с уровнем одного периода, принятого за базу. Они называются базисными.

Пример. - уровни явления за одинаковые последовательные периоды. Тогда цепные темпы роста находят по формулам:

А базисные темны роста по формулам:

если за базу сравнения принят период .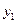

Таблица 1. Величина импорта Томской области в млн. руб.

	импорт	темп роста цепной	темп роста базисный	темп прироста цепной	темп прироста базисный
	197,9
		72,76%	72,76%	-27,24%	-27,24%
	253,2	175,83%	127,94%	75,83%	27,94%
	94,1	37,16%	47,55%	-62,84%	-52,45%
	80,3	85,33%	40,58%	-14,67%	-59,42%
	56,4	70,24%	28,50%	-29,76%	-71,50%
		120,57%	34,36%	20,57%	-65,64%
	44,6	65,59%	22,54%	-34,41%	-77,46%
Итого	938,5

То есть величина импорта снизилась в 1998 году на 62,84% по сравнению с 1997, на 59,42% в 1999 году по сравнению с 1995 и увеличился на 27,94% в 1997 году по сравнению с 1995.

При определении относительных показателей динамики важно обеспечить сопоставимость показателей,которые участвуют в расчете. Несопоставимость может возникнуть по многим причинам: меняется методология расчета показателей или степень охвата совокупности, показатели относятся к периодам разной продолжительности и т.д.

К относительным показателям динамики относятся также показатели выполнения плана, по которым судят о ходе реализации различных программ как на национальном и региональном уровнях, так и на уровне фирмы. В этом случае относительная величина получается как результат сопоставления фактической и плановой абсолютных величин, относящихся к одному и тому же периоду.

Относительная величина планового задания(ОВПЗ) равна отношению величины показателя по плану к его фактической величине в предшествующем периоде:

.

Относительная величина выполнения плана (ОВВП) равна отношению фактической (отчетной) величины показателя к запланированной на тот же период его величине:

.

Пример. В первом квартале предприятие выпустило 15370 единиц продукции, на второй квартал было запланировано выпустить 16000 единиц продукции, а выпустили только 15840 единиц. Вычисли относительные величины:

Планового задания: ; то есть было запланировано увеличить производство на 4,1%.

Выполнения плана: , то есть план не выполнен на 1%.

Относительные величины планового задания, выполнения плана и темпы роста связаны между собой: произведение ОВПЗ и ОВВП равно темпам роста.

.

Для рассмотренного примера: .

Относительные величины интенсивностиполучают, сопоставляя разноименные признаки одной совокупности, а также объекты двух связанных между собой совокупностей.

Примерами такого рода показателей могут служить коэффициент рождаемости (число родившихся в расчете на 1000 человек населения), уровень занятости (отношение числа занятых к численности экономически активного населения). Здесь показатели интенсивности получены как отношение значений различных признаков одной совокупности. Эти показатели обычно выражаются в процентах, промилле и т.д.

К показателям интенсивности, полученным на основе разных совокупностей, относятся плотность населения (число людей, приходящихся на 1 кв. км территории), фондоотдача (стоимость продукции, произведенной на 1 руб. основных фондов) и т.д. В этом случае единицы измерения относительных величин интенсивности определяются показателями, на основе которых они рассчитаны.