Решение краевых задач для одномерного волнового уравнения методом разделения переменных (Фурье)
Эта задача интерпретировать малые поперечные колебания струны без воздействия внешних сил (свободные колебания), струна имеет конечную длину 0 ≤ x ≤ l, в каждой точке этой струны задано начальное ее отклонение равновесного положения и начальная скорость. Будем пока считать, что концы струны жестко закреплены, что соответствует краевому условию
Будем искать решение поставленной задачи
, тогда
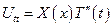и 
поставим эти уравнения в начальное уравнение.
для того, чтобы проинтегрировать раздел. переменные
поскольку последнее равенство выполнено для любых значений Х и Т, то найдется такое число К, что
из краевых условий 
=> 
=> 
Следовательно, для нахождения функций Х(х) и Т(t) получаем две задачи
1-ый случай: К > 0, тогда
, где С1, С2, С3, С4 – произвольные постоянные.
Система однородная, определитель ≠ 0.
Полученная система на С3 и С4 будет иметь отличное от нуля решение только в том случае, если определитель = 0.
К = 0, что противоречит, что К = 0.
2-ой случай: К = 0
=> 
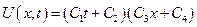
3-ий случай: К < 0
Положим 
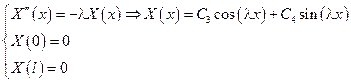
– собственные значения поставленной задачи штурма – Муввиля, каждая из которых:
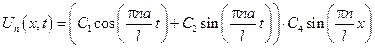
Пользуясь принципом суперпозиции решения однородных задач, получаем, что общее решение будет иметь вид:
Для определенных коэффициентов An и Bn воспользуемся начальными условиями
– ряд Фурье.
Функция f(x) по синусам, а An – коэффициент ряда Фурье по функциям f(x).
– это разложение функции g(x) в ряд Фурье.
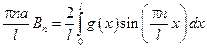
Пример: Тугонатянутая гибкая струна. Книга Троицкой, стр. 23, задача 4
«Смешанная задача для волнового уравнения в прямоугольнике»
, где S – граница области, в которой ищется решение.
Пусть теперь мембрана имеет вид прямоугольника.
воздействие внешних сил не учитываем
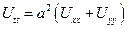
Применим метод разделения переменных
Подставим эти выражения для производных в исходное уравнение:
разделим это равенство на
получим:
Причем последнее равенство выполнено для любых точек x, y, t => существует постоянное число λ, такое что
Причем, последнее равенство выполнено при любых x и y => найдутся числа λ1 и λ2 такие что:
λ = λ1 + λ2 и
, а 
Из граничных условий:
для любых точек x и t =>
Y(0) = 0
для любых точек y и t =>
X(l) = 0
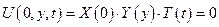для любой точки y, t =>
X(0) = 0
для любой точки x, t =>
Y(m) = 0
Следовательно, получаем две задачи Штурма – Люнвина для нахождения функций X(x) и Y(y).
Задачи:
1. Пусть λ1 > 0, тогда
C1 = C2, т.к. 
λ1 > 0 быть не может
| 
1. Аналогично левому столбику, можно показать, что λ2 > 0 быть не может
|
2. λ1 = 0 X(x) = ax + b
 b = 0
 a = 0
λ1 ≠ 0
решение тривиальное
| 2. Аналогично λ2 ≠ 0 |
3. λ1 < 0
Характеристическое уравнение
С1 = 0
 – бесконечно много собственных значений задачи Штурмана – Люнвина
| λ2 < 0
Характеристическое уравнение
 С3 = 0
 
 – бесконечно много собственных значений
|
Каждое из найденных собственных значений порождает собственную функцию
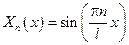
Следовательно:
Найдем T(t)
Характеристическое уравнение:
– бесконечное число собственных функций задачи Штурмана – Люнвина, на нахождение функции T(t), тогда общее решение исходной задачи будем искать в виде:
где Ank и Bnk – определяются, исходя из начальных условий
Не трудно показать, что система функций
– ортогональная система функций на прямоуг
Bnk – коэффициент Фурье, разложения функции f(x,y) в ряд Фурье по этой системе =>
Воспользуемся заданной начальной скоростью для нахождения коэффициента Ank.
откуда получаем, аналогично предыдущему, что
– коэффициент Фурье разложения функции g(x,y) в ряд Фурье по системе функций
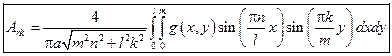
22 вариант (14)
|
U(t,x,y,z) – температура в точке 
в момент времени t.
Воспользуемся законом Фурье для плотности потока тепла W в направлении нормали 
в единицу времени.
, где 
– производная функции температуры U(t,x,y,z) вдоль нормали , k – коэффициент теплообмена.
k – может быть функцией температуры, точки, времени, т.е.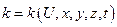 
.
Рассмотрим часть тела V ограниченную поверхностью S.
Напишем уравнение баланса тепла в объеме D за малое время Δt.
– где М – точка объема D – функция плотности тепла от внешних источников, тогда Q1 – количество тепла от внешних источников.
– количество тепла, пришедшее в объем D за счет внешних источников за время Δt.
– расход тепла за счет выходящего из D потока.
– изменение количества тепла в области D за время Δt, где
С(x,y,z) – теплоемкость тела (вещества) в точке x,y,z;
ρ(x,y,z) – плотность вещества;
Ut(x,y,z,t) – изменение температуры.
Уравнение баланса тепла по закону сохранения энергии имеет вид:
Q3 = Q1 – Q2
или в интегральной форме
(*)
U(x,y,z) 
где 
Поток векторного поля через поверхность S:
– теорема Остроградского – Гаусса.
Применим теорему Остроградского – Гаусса к последнему интегралу (*).
,
тогда уравнение теплового баланса приобретает вид:
Последнее равенство выполнено для любой области D, целиком лежащей в объеме V; в виду произвольности области D, получаем уравнение теплопроводности:
уравнение теплопроводности, уравнение распространения тепла в объеме V.
ρ, C, k – функции от М(x,y,z) и времени t;
k – коэффициент теплообмена (Фурье).
Интересный случай, когда среда однородная, т.е. ρ, C, k – постоянные и не зависят ни от положения точки, ни от времени, тело – однородно и его характеристики с течением времени не меняются, тогда
, обозначим 
– получим =>
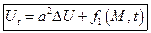уравнение теплопроводности для однородного тела.
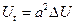– однородное уравнение теплопроводности.
– волновое уравнение.
Уравнения теплопроводности принадлежат к классу уравнений параболического типа.
Доказательство:
Совершенно аналогично выводится уравнение диффузии.
Воспользуемся законом Нернста для потока вещества W в направлении .
U(M,t) – концентрация диффундированного вещества в точке М объема V в момент времени t.
, где
D – коэффициент диффузии.
f(M,t) – количество вещества, попадающего в точку М от внешних источников.
- диффунд. из тела, выходящий поток в-ва
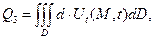где
d – коэффициент пористости среды, в котором происходит диффузия
Аналогично пред. можно показать, что из уравнения:
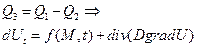
Уравнение диффузии, отлич. от уравнения теплопроводн. только тем, что коэффициенты D и d имеют другой физический смысл, если считать, что среда однородная, то уравнение приобретет вид
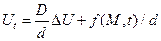, обозначим 
Функция конечного вещества
Уравнение диффуз и распространенного тепла в некотором объеме одинаковы.
В 1-ом случае:
U(M,t) – конц. вещества в V
2-ом U(M,t) - темпер.
Уравнение теплопроводн. имеет множество решений, чтобы было единственным нужно задать начальные и краевые условия