Операции над бинарными отношениями.
Так как отношения на X задаются подмножествами, aÍX´X, для них определены те же операции, что и над множествами.
Возьмем два отношения α и b. Каждому из них соответствует некоторое множество пар (подмножества aÍX´X и bÍ X´X).
Определение 3.14. Пересечением отношений αÇb называется отношение, определяемое пересечением соответствующих подмножеств.
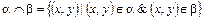
Ясно, что x(αÇb)y выполнено тогда и только тогда, когда одновременно выполнены соотношения xαy и xby.
Пример. Пусть X - множество вещественных чисел, α - отношение "быть не меньше", b - отношение "быть строго больше". Тогда αÇb есть отношение "быть строго больше".
Определение 3.15. Объединением отношений αÈb называется отношение, определяемое объединением соответствующих множеств.
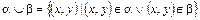
Соотношение x(αÈb)y выполнено тогда и только тогда, когда выполнено хотя бы одно их соотношений xαy или xby.
Пример. Если α – отношение "больше" на множестве чисел, а b – отношение "равно", то αÈb – это отношение ≥.
Определение 3.16. Обратным отношением называется отношение, определяемое условием: 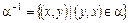 .
.
Пример. Пусть α – отношение "делит", тогда α-1 – отношение "делится".
Определение 3.17. Разностью будем называть отношение, удовлетворяющее условию 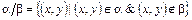 .
.
Определение 3.18. Разностью будем называть отношение, удовлетворяющее условию 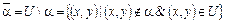 , где U
, где U
Определение 3.19. Составное отношение (композицией) называется отношение, определяемое следующим образом:  .
.
Пример. Пусть α – отношение "быть женой", а b – отношение "быть отцом". Что означает в этом случае соотношение хαbу? По определению существует такой z, что "x - жена z" и "z - отец y". Другими словами, "x есть жена отца y", т.е. "x - мать или мачеха y".
Пример. Пусть α – отношение "быть братом", а b – отношение "быть родителем". Тогда произведение αb есть отношение "быть братом одного из родителей", т.е. "быть дядей".
Лемма 3.2. Если отношения α и b рефлексивны, то рефлексивны и следующие отношения: αÇb, αÈb, α-1, αb.
Лемма 3.3. Если отношения α и b симметричны, то симметричны и следующие отношения: αÇb, αÈb, α-1.
Лемма 3.4. Чтобы составное отношениеαb симметричных отношений α и b было симметрично, необходимо и достаточно, чтобы отношения α и b коммутировали.
Лемма 3.5. Если отношения α и b – антисимметричны, то антисимметричны также и следующие отношения: αÇb, α-1.
Антисимметричность может не сохраняться при объединении и композиции.
Лемма 3.6. Если отношения α и b транзитивны, то транзитивны также следующие отношения: αÇb, α-1.
Из лемм 3.2, 3.3, 3.4, 3.5 вытекают следующие две теоремы.
Теорема 3.6. Если α и b – строгие порядки (нестрогие порядки), то пересечение αÇb также является строгим порядком (нестрогим порядком).
Замечание. Пересечение строгого и нестрогого порядка есть строгий порядок.
Свойство "быть линейным порядком" не обязано сохраняться при пересечении. Это проще всего увидеть из следующих соображений. Пусть a – линейный порядок (строгий или нестрогий), тогда αÇα-1=Æ (или =E). Значит, αÇα-1на множестве более чем из одного элемента не является линейным порядком.
Теорема 3.7. Если отношение α является строгим (нестрогим, линейным) порядком, то и отношение α-1 является строгим (нестрогим, линейным) порядком.
Объединение порядков в общем случае не является порядком. Это хорошо видно на таком примере. Пусть α – линейный нестрогий порядок, тогда α-1 – есть отношение того же типа. Однако, объединение αÈα-1 есть полное отношение, и, следовательно, не является порядком. Ниже приведены без доказательства условия, при которых объединение порядков является порядком.
Теорема 3.8. Если α и b – строгие порядки, то объединение αÈb является строгим порядком в том и только том случае, когда  .
.
Теорема 3.9. Для того чтобы объединение αÈb нестрогих порядков α и b было нестрогим порядком, необходимо и достаточно выполнение условий  ,
, 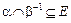 .
.
Композицией порядков αb также не обязано быть порядком. Это видно из того хотя бы, что для линейного нестрогого порядка α композиция  есть полное отношение. Достаточным условием является, например, такое.
есть полное отношение. Достаточным условием является, например, такое.
Теорема 3.10. Если α и b – строгие порядки и выполнены соотношения: 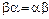 ,
, 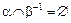 , то αb – строгий порядок.
, то αb – строгий порядок.