Многоместные отношения. Композиция отношений. Степень и ядро отношений.

Понятие многоместного отношения является обобщающим понятием отношения и его называют n-местным или n-арным отношением.

Определение 2.5. n-местным отношением называется любое подмножество множества Аⁿ, где А – произвольное множество, n ³ 1. Двухместное отношение называют бинарным.

Многоместное отношение используется, например, в теории баз данных.

Пример.: R Ì A₁ ´ A₂ ´ … ´ A_n = {(a₁, a₂, … ,a_n) | a₁ Î A₁ & a₂ Î A₂ & … a_n Î A_n}.

A₁ = A₂ = … = A_n = A

Пусть R₁ Ì A ´ C, а R₂Ì C ´ B. Композицией двух отношений R₁ и R₂ называется отношение R Ì A ´ В, определяемое следующим образом:

R:=R₁ 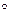R₂:={(а,b) | a Î A & bÎ B &$ cÎ C & aR₁c & cR₂b}

Композиция отношений на множестве А является отношением на множестве А.

 

Пусть R – отношение на множестве А.

Определение 2.6. Степенью отношения R на множестве А называется его композиция с самим собой. Rⁿ := R … R

Соответственно: R⁰ = 1; R¹ = R; R² = R 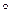R и вообще Rⁿ = R 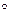R^n-1

 

Если R – отношение из А в В, то есть R Ì A ´ B.

Определение 2.7. Композиция отношения R 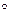R^-1 называется ядром отношения R.

Ядро отношения R из А в В является отношением на множества А.

Свойства отношений.

Пусть R – есть отношение на множестве А: R Ì A ´ А | a , b Î A

Введем следующие понятия:

1)обратное отношение: R^-1:={(a,b)|(b,a)ÎR};

2) дополнение отношения: := {(a,b)|(a,b) Ï R };

3) тождественное отношение: I:= {(a,a)|aÎ R};

4) универсальное отношение: U:= {(a,b) | aÎA & bÎA}.

Замечание: пусть R – отношение на множестве А (R Ì А²), тогда:

Если " аÎА, аRа, то отношение R называется рефлексивным.

Если " аÎА, аRа, то такое отношение R называют антирефлексивным.

Если " а,bÎА, аRb Þ bRа. Такое отношение R называют симметричным.

Если " а,bÎА, аRb & bRа Þ a=b. Такое отношение R называют антисимметричным.

Если " а,b,сÎА, аRb & bRс Þ аRс. Такое отношение R называют транзитивным.

Если " а,bÎА, а¹bÞ aRb Ú bRa. Такое отношение R называют полным (линейным).

Теорема: пусть R – отношение на множестве А, то есть RÌA´А, тогда:

отношение R рефлексивно тогда и только тогда, если тождественное отношение включается во множество R.

отношение R симметрично тогда и только тогда, когда R = R^-1 (равно обратному отношению).

отношение R транзитивно тогда и только тогда, когда композиция отношений R·RÌR (включается в отношение R).

отношение R антисимметрично тогда и только тогда, когда пересечение отношения R с обратным отношением включается в тождественное отношение: RÇR^-1Ì I.

отношение R антирефлексивно тогда и только тогда, когда пересечение отношения R с тождественным отношением I образует пустое множество: R Ç I = Æ.

отношение R полно тогда и только тогда, когда объединение отношения R с тождественным отношением I и с обратным отношением образует полное отношение U:

R È I È R^-1 = U.

Для операции композиции отношений существуют две теоремы, позволяющие оценить результат:

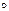
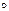
Теорема: = | ( )_{[i, j]}:= _{[i, k]}& _{[k, j]}

Теорема: = È | ( È )_{[i, j]}:=R_{1 [i, j]} Ú R_{2 [i, j]}

 

Пример

Пусть есть множества А и В, на которых заданы отношения δ и ρ соответственно, и

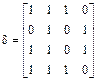
, то композиция отношений

 

Представление отношений в ЭВМ.

Пусть R – отношение на А (R Ì A ´ A) и |А|=n, тогда отношение R можно представить матрицей R:array[1…n,1…n] of 0…1, где

Матрица - матрица отношений.

Тема 3. Специальные классы отношений. Отношение эквивалентности и разбиения. Отношения порядка. Минимальные элементы. Теорема о существовании минимального элемента. Алгоритм топологической сортировки. Операции над бинарными отношениями.