Основные понятия теории множеств. Способы задания множеств
Тема 1. Основные понятия теории множеств. Способы задания множеств. Диаграммы Венна. Операции над множествами. Свойства теоретико-множественных операций. Представление множеств в ЭВМ.
Основные понятия теории множеств. Способы задания множеств
Определение 1.1. Множество – это любая, определенная совокупность объектов. Объекты из которых составлено множество называют его элементами. Элементы множества различны и отличны друг от друга. Множества обозначают прописными буквами латинского алфавита, а их элементы – строчными. Например N, Z, Q, R – множества натуральных, целых, рациональных и действительных чисел.
N={1, 2, 3…} A={a1, a2, a3…}
Если объект х является элементом множества М, то говорят, что хÎМ. Если х не является элементом множества М, то говорят, что хÏМ.
Одно множество равно другому, если выполняется условие: A=B | A 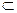 B & B
B & B 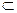 A
A
Множество не содержащее элементов называется пустым. Его обозначают Ø.
Обычно, в конкретных обсуждениях, элементы всех множеств берутся из некоторого одного достаточно широкого множества U (своего для каждого множества), которое называется универсальным множеством или универсумом. В общем случае множества могут быть конечными и бесконечными. Конечное множество – это такое множество, для которого существует натуральное число, равное количеству элементов множества, и называемое мощностью множества и обозначаемое |A|.
Чтобы задать множество нужно указать, какие элементы ему принадлежат. Это можно сделать различными способами:
1)перечислением элементов множества А={a1, a2,…, an|n=6} (перечислением можно задавать только конечное множество);
2) характеристическим предикатом M={ x | P(x) }, где P(x) – предикат.
Характеристический предикат – это некоторое условие, выраженное в форме логического утверждения, возвращаемое логическое значение. Если для данного элемента условие выполнено, т.е. P(x) = 1, то этот элемент принадлежит определяемому множеству, в противном случае – не принадлежит. Пример 1.1.:
M = { x | xÎN & x < 10}
P(x) = (11) = ( 11 & 11 < 10 ) = 0 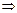 11ÏМ
11ÏМ
3) порождающей процедурой: M={ x | x := f }
Порождающая процедура – это процедура, которая будучи запущенной порождает некоторые объекты, являющиеся элементами порождаемого множества.
Иначе говоря, порождающая процедура – последовательность действий, которые формируют некоторые объекты по заданному правилу.
Пример 1.2.: M = { x | x := from 1 to 9 generate x}