Полуограниченные турбулентные струйные течения

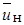В качестве примера полуограниченной струи рассмотрим основные закономерности изобарической струи, вытекаю­щей параллельно гладкой стенке (рис. 10.8) из плоской ще­ли шириной . С другой стороны струя соприкасается с безграничным потоком окружающей среды, скорость кото­рой меньше начальной скорости струи Изучая разви­тие такой струи, В. Е. Грум-Гржимайло впервые отметил явление настильности, суть которого заключается в уве­личении ее дальнобойности вследствие уменьшения объ­ема подсасываемого в струю газа из окружающей среды.

Рис. 10.8. Схема полуограниченной турбулентной струи при u₀ > u_н: 1, 2 - - внутренняя и внешняя границы струйного пограничного слоя

 

 

Для простоты допустим, что внешняя среда и струя имеют одни и те же физиче­ские свойства и являются несжимаемыми. Будем счи­тать также, что в началь­ном сечении на свободной границе происходит изменение скорости от 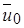до 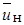и толщина пограничного слоя на стен­ке равна нулю, т.е. пограничный слой на обеих границах струи начинает развиваться в начальном сечении OO’. В се­чении, где осуществляется смыкание струйного погранич­ного слоя и пограничного слоя на стенке, заканчивается начальный участок течения, длина которого обозначается, как и ранее, .

В сечении с координатой х_п начинается основной уча­сток струи, в котором осевая скорость изменяется от значения 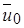до 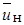. Область течения между сечениями с ко­ординатами х_н и х_п представляет собой переходный учас­ток, толщина струи в котором нарастает примерно по тому же закону, что и в начальном участке.

Таким образом, условия развития полуограниченной струи, распространяющейся параллельно твердой поверх­ности, отличаются от гидродинамической обстановки в вер­хней половине свободной струи, развивающейся во встреч­ном или в спутном потоках, лишь одним фактором: наличием пристенного пограничного слоя. Поэтому для на­чального участка полуограниченной струи остаются спра­ведливыми вышеприведенные уравнения. Длина начально­го участка такой струи находится из условия смыкания внутренней границы пограничного слоя и границы при­стенного пограничного слоя d, т.е.

(10.45)

где - толщина пристенного пограничного слоя в кон­це начального участка. Если для описания профиля скоро­сти в этом слое выбрать степенной закон (см. гл. 7) и участь, что на начальном участке то для определения толщины пограничного слоя можно воспользоваться выражением где Поскольку безразмерная величина зависит от , то длину начального участка находят по уравнению (10.45) методом последовательных приближений.

Заметим, что в общем случае начальный участок полуограниченной струи короче, чем в свободных струях. Так, на­пример, при m = 0 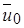= 50 м/c и b₀ = 0,02 м, х_н = 7,2b₀ , в то время как для затопленной свободной струи х_н @ 9b₀. Напротив, длина переходного участка полуограниченной струи существенно больше, чем свободной. Она определя­ется по формуле

(10.46)

где причем

Для приведенных выше условий расчета 20,5, тогда как для затопленной свободной струи @1,5; 13,5.

Относительный расход газа, протекающего через попе­речное сечение полуограниченной струи в начальном участ­ке описывается выражением (10.35), в правой части которого появляется дополнительное слагаемое d/(7 ) или 0,053 x/ Влияние этого слагаемого на весьма не­значительно. Так, например, в конце начального участка при m = 0, 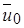= = 50 м/c и b₀ = 0,02 м оно составляет всего 0,027.

В пределах основного участка полуограниченной струи профиль скорости газа описывается двумя уравнениями: степенного закона при и Шлихтинга, в котором координата у отсчитывается от границы пристенного по­граничного слоя d, т.е. Тогда уравнение со­хранения количества движения

после использования вышеуказанных профилей и вычисле­ния интегралов можно записать в виде:

(10.47)

где Решая это квадратное уравнение, нахо­дим связь максимальной скорости в струе с локальной тол­щиной слоя смешения b

(10.48)

где

Учитывая, что согласно многочисленным эксперименталь­ным данным

(10.49)

в результате совместного решения системы уравнений (10.36), (10.48) и (10.49) находим:

(10.50)

(10.51)

где

Для затопленной полуограниченной струи (m = 0) из уравнения (10.47) с учетом соотношения (10.49) получаем или, поскольку b =c x = 0,22 x,

Сопоставляя этот результат с уравнением для затоплен­ной струи, видим, что максимальная скорость полуограниченной струи убывает с ростом х по тому же самому зако­ну, что и свободной, хотя при равных значениях х в первом случае несколько ниже. Это объясняется тем, что от­носительный расход газа через поперечное сечение струи в основном участке

(10.52)

лишь немногим отличается от половинного расхода свобод­ной струи (величина 0,0875).

Аналитического расчета для полуограниченных струй, распространяющихся из сопел сложного профиля до сих пор не получено.

Экспериментальное изучение подобного рода течений по­казало, что профиль скорости в пристенном пограничном слое настильной струи "полнее", чем профиль скорости в пристенном пограничном слое, образующемся при обте­кании пластины безграничным потенциальным потоком; распределение усредненной скорости в пограничном слое определяется степенным законом при показателе степени n = 10 ¸ 14, а не при n = 7.

Так же как и для неограниченной свободной турбулент­ной струи, профили скорости основного участка струи практи­чески подобны.

О форме осесимметричной струи вытекающей парал­лельно гладкой стенке можно судить по опытным данным В. И. Миткалинного, представленным на рис. 10.9. На уров­не оси струи в горизонтальной плоскости (рис. 10.9,а) внешняя граница остается практически прямолинейной на уча­стке, длина которого составляет около 10d₀ от начального сечения. При этом угол раскрытия границы струи (рис. 10.9,б) на этом участке составил 7,5^о, тогда как для свободной струи он равен 10^о. Угол раскрытия струи непосредственно у плоскости составил »15^о. После поперечного сечения, отстоящего от начального сечения на расстоянии 11,0, граница полуограниченной струи искривляется. Форма поперечного сечения начальной струи показана на рис. 10.9,в.

Рис. 10.9. Схема изменения формы настильной струи в горизонтальной

плоскости (а), на границе (б) и в начале (в)

 

На рис. 10.10 представлена зависимость относительной ско­рости в поперечных сечениях полуограниченной струи.

Рис. 10.10. Зависимость относительной скорости в поперечном сечении полуограниченной струи

 

 

Представленные результаты указывают на отличие профиля относи­тельной скорости свободной затопленной струи от профиля настильной струи, поскольку при 1,5 опытные точки настильной струи располага­ются выше, чем свободной. Во внешней области (в верти­кальной плоскости) профи­ли скоростей ограниченной и затопленной струи совпа­дают.

Если струя бьет в стенку под углом a (рис. 10.11), то при этом наблюдается рас­текание струи, величина ко­торого пропорциональна углу атаки a. В результате про­исходящей при этом непре­рывной деформации струи максимум скоростей прибли­жается к стенке.

м/с

Рис. 10.11. Изменение скорости в поперечных сечениях (0 – IV)

струи, направленной на стенку под углом a

 

Удельное давление р_a, оказываемое струёй на стенку, зависит от угла атаки и определяется соотношением где F - поперечное сечение струи; - количество движения до растекания на стенке.

Для случая распределения скорости в поперечном сече­нии струи по закону треугольника, в пределах угла атаки a = 10 ¸ 40^о В. И. Миткалинным предложено следую­щее уравнение для определения величины удельного давле­ния

Вследствие расплющивания струи, атакующей стенку под углом a, относительная поверхность контакта струи с окружающей средой увеличивается, а дальнобойность ее уменьшается с возрастанием угла атаки.

Для угла атаки a = 90^о т.е. равно удвоенному динамическому давлению.

В заключение отметим, что, используя современные ин­женерные теории турбулентности, численные методы ана­лиза и ЭВМ, можно решать весьма сложные задачи струй­ных течений, сопровождающихся процессами горения и тепломассообмена в любом случае. Однако математические модели металлургических печей и установок должны учи­тывать те закономерности теории струй, элементы которой рассмотрены выше.

Пример 10.3. Определить параметры полуограниченной струи, развивающейся в спутном потоке вдоль плоской стенки при условиях: r = 1,3 кг/м³; 50 м/с; b₀ = 0,02 м; h = 15×10^-6 Па×с.

Используем для решения задачи пакет Mathcad(см. ниже).