Краткие сведения из теории ошибок измерений

Измерения на местности являются важной частью всех геодезических работ. Любые измерения сопровождаются ошибками. Различают следующие виды ошибок: грубые, си­стематические и случайные. Грубые ошибки измерений или промахи должны быть выявлены и исключены. С этой целью выполняются повторные измерения и вычисления. Систе­матические ошибки возникают в результате влияние какой-то причины. Например, из-за неисправности инструмента. Источник систематической ошибки необходимо выявить и устранить.

Случайные ошибки являются следствием влияния раз­личных факторов. Закономерность возникновения случайных ошибок при небольшом ряде измерений не обнаруживается.

Исследованиями установлены следующие свойства слу­чайных ошибок:

1. по абсолютному значению они не превосходят опреде­ленной величины, соответствующей данным условиям изме­рений,

2. положительные и отрицательные случайные ошибки встречаются одинаково часто,

3. чем больше абсолютная величина случайной ошибки, тем реже она встречается в данном ряду измерений,

4. с увеличением числа измерений среднее арифметичес­кое из случайных ошибок стремится к нулю.

На основании четвертого свойства случайных ошибок можно утверждать, что среднее арифметическое из резуль­татов измерений одной и той же величины — ℓ₀ будет близко к истинному значению этой величины — ℓ. Среднее арифме­тическое из результатов измерений — ℓ₀ равно:

где [ℓ ] — сумма результатов n измерений одной и той же величины.

 

В теории вероятностей среднее арифметическое ℓ₀ при­нимается за вероятнейшее значение измеряемой величины. Вероятнейшей ошибкой одного измерения 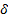_i считается от­клонение результата измерения от вероятнейшего значения:

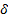_{I =} ℓ_{i -} ℓ_0,

где i — текущий номер измерения.

Основным критерием при оценке точности измерений в России принята средняя квадратическая ошибка — m.

Для характеристики точности вычисляется средняя квад­ратическая ошибка одного измерения по формуле:

m = √[Δ²]/n,

где Δ — случайная ошибка одного измерения, [Δ²] — сумма квад­ратов случайных ошибок, n — число измерений. Однако, слу­чайную ошибку одного измерения найти трудно, т.к. как прави­ло, неизвестно истинное значение измеряемой величины. По­этому среднюю квадратическую ошибку одного измерения под­считывают по вероятнейшим ошибкам — 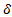по формуле:

m = √[ 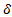²]/n-1

где [ 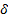²] — сумма квадратов вероятнейших ошибок, n — число измерений, n— 1 — число избыточных измерений.

Для характеристики точности вероятнейшего значения измеренной величины, т.е. точности арифметической среди­ны, используется формула:

M = m/√n= √[δ²]/n(n-1),

 

Очевидно, что средняя квадратическая ошибка арифме­тической средины — М меньше средней квадратической ошибки одного измерения в √n раз. Поэтому целесообразно измерять одну и ту же величину многократно, чтобы повы­сить точность измерений. Однако, при большом числе избы­точных измерений возрастает влияние остаточных система­тических ошибок. Установлено, что оптимальное число по­вторных измерений примерно равно 8—10.

Необходимо учитывать, что критерии оценки точности измерений m и М не безошибочны, т.к. их точность зависит от числа измерений n.

Средние квадратические ошибки самих средних квадратических ошибок m и М равны:

m_m = m/√2(n-1)

M_m = m_m/√n = m/√2n(n-1)

Теорией вероятностей установлены предельные величи­ны случайных ошибок измерений — Δ_пред :

Δ_пред. = Зm или Δ_пред.= 2m

Точность измерения линий, площадей и некоторых дру­гих величин характеризуют относительной ошибкой, пред­ставляющей собой отношение средней квадратической ошиб­ки к измеренной величине. Такое отношение выражается в виде простой дроби с числителем 1, т.е. :

m_ℓ/ℓ = 1/N,

где N = ℓ/m₁

 

Например, средняя квадратическая ошибка измерения линии длиной 60 м составила 0,05 м. Относительная ошибка измерения равна 0,05 / 60 = 1/ 1200.

Пример оценки точности измерений. Вычислить веро­ятнейшее значение длины линии по данным 7 измерений (табл. 2) и оценить точность измерений.

 

Таблица 2. Пример оценки точности измерений

№№	ℓ, м	δ, см	δ2, см2
	67,84	-1,3	1,7
	67,86	+ 0,7	0,5
	67,82	-3,3	10,9
	67,85	-0,3	0,1
	67,88	+ 2,7	7,3
	67,87	+ 1,7	2,9
	67,85	-0,3	0,1

ℓ ₀= 67,853 [δ]= -0,1 [δ²] = 23,5

m = ±√23,5 /6 = ±1,98 cм

m_m = ± 1,98 / √12 = ±0,57 cм

M = ±1,9 / √7 = ±0,75 cм

M_M = ± 0,57/√7 = ± 0,22 cм

 

Очевидно, что в данном ряду измерений отсутствует ошибка, превышающая Δ_пред. Вероятнейшее значение длины измеренной линии: 67,853 ± 0,0075 м. Средняя квадратичес-кая относительная ошибка этого значения равна: М/ ℓ₀ = 0, 0075/67,853 - 1/ 9047.

Средняя квадратическая ошибка функции измеренных величин

В практике геодезических работ возможны случаи, когда определяемая величина является функцией непосредствен­но измеренных величин. В таких случаях для оценки точно­сти определяемой величины используются средние квадра-тические ошибки непосредственно измеренных величин.

В теории ошибок измерений выведены формулы. Ниже приведены некоторые из этих формул.

1. Простая линейная функция вида: и = х + у + ...+ ω

Средняя квадратическая ошибка функции ти2 равна:

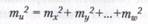
В частном случае при : m_x ⁼ m_y + …+ m_{ω =} m, получим: m_u = m√n, где n — число измеренных величин.

Пример. Одним и тем же теодолитом, в равных условиях измерены 3 горизонтальных угла треугольника. Средняя квадратическая ошибка одного измерения угла равна 1 ми­нуте. Средняя квадратическая ошибка суммы измеренных углов треугольника равна: n=1’√З=1,7'.

2. Произведение независимых измеренных величин.

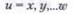
В этом случае:

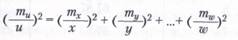
Таким образом, для оценки точности произведения неза­висимых измеренных величин следует суммировать квадраты относительных средних квадратических ошибок измерений.

3. Функция многих независимых переменных общего вида:

Средняя квадратическая ошибка функции данного вида равна:

 

 

— квадраты частных производных функции по каждой переменной, m_х²,m_у²,...,m_ω²- средние квадратические ошибки непосредственно измеренных величин. В ряде случаев для оценки точности геодезических и фо­тограмметрических работ применяют метод двойных изме­рений.Каждую определяемую величину измеряют дважды. При этом измерения выполняются в равных условиях и из результатов измерений исключаются грубые и систематичес­кие ошибки. Среднюю квадратическую ошибку одного изме­рения подсчитывают по разностям двухкратных измерений ряда величин по формуле:

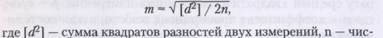
ло измеренных величин.

Пример. В табл. 3 даны результаты фотограмметричес­ких измерений памятника архитектуры: координаты x: точек на снимке измерены дважды — х и х'. Определить среднюю квадратическую ошибку одного измерения.

Таблица 3. Расчет средней квадрата ческой ошибки одного измерения

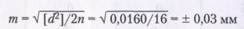
Понятие веса.В практике геодезических работ измере­ния выполняются в разных условиях. Например, использу­ются неодинаковые по точности приборы, или работа ведет­ся в разных погодных условиях и разными исполнителями. Такие измерения называются неравноточными в отличии от равноточных. При обработке данных неравноточных изме­рений вводится понятие веса —р. Это число, которое обозначает степень надежности результата измерения. Например, имеется ряд измеренных величин: ℓ₁, ℓ_2, ℓ₃,…ℓ_n с весами p₁, p₂, p₃,…p_n. Для приведения неравноточных измерений к равно-результат каждого измерения умножается на его вес:

Вес результата измерения обратно пропорционален квадрату средней квадратической ошибке измерения: 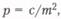где с — коэффициент пропорциональности, некая постоянная величина.

Для оценки точности неравноточных измерений определяется средняя квадратическая ошибка единицы веса т по формуле:

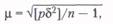
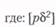— сумма произведений квадратов вероятнейших ошибок и их весов, п — число измерений.

Средняя квадратическая ошибка отдельного измерения 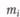равна:

Средняя квадратическая ошибка среднего весового зна-чения равна:

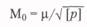
Пример.Вычислить среднее весовое значение длины ли-нии и выполнить оценку точности измерений.