II. Список теоретических вопросов к экзамену
Высшая математика II семестр
I. Учебный план занятий
| Менеджмент | социология | ||
| 1. | 9.02 | Понятие первообразной и неопределённого интеграла Основные свойства неопределённого интеграла Непосредственное интегрирование | |
| 2. | 19.02 | Интегрирование методом замены | |
| 3. | 26.02 | Интегрирование по частям. Интегрирование рациональных дробей. | |
| 4. | 5.03 | Интегрирование рациональных дробей. Интегрирование простейших иррациональных дробей | |
| 5. | 12.03 | Интегрирование тригонометрических функций. Повторение. | |
| 6. | 19.03 | Определённый интеграл. Контрольная работа №2. (домашняя - принимаю) | |
| 7. | 26.03 | Контрольная работа №1 | |
| 8. | 2.04 | Числовые ряды | |
| 9. | 9.04 | Степенные ряды | |
| 10. | 16.04 | Комплексные числа | |
| 11. | 23.04 | Контрольная работа №3-4 | |
| 12. | 30.04 | Анализ итогов и ошибок по К.р. №1-2 | |
| 13. | 7.05 | Анализ итогов и ошибок по К.р. №3-4 | |
| 14. | 14.05 | Перенос | |
| 15. | 21.05 | перенос | |
| 16. | 28.05 | перенос | |
| 1.06-7.06 | Зачетная неделя | ||
| 8.06-28.06 | экзамены |
II. ТЕКУЩИЙ КООНТРОЛЬ
Контрольная работа №1
| В-т | Неопределенные интегралы №1 53 балла | |||||||||||||||||||||
Контрольная работа №2
| В-т | Определенные интегралы №2 домашняя 12 баллов | ||||||
Контрольная работа №3
| № В-та | Ряды№3 20баллов | |||
Контрольная работа №4
| № В-та | Комплексные числа №4 15 баллов | ||||||
| 0,5 | 0,5 | ||||||
Таблица корректировки баллов в зависимости от сложности варианта:
| 1-10 вариант | 11-40 вариант | 41-50 вариант | |
| Неопределенные интегралы №1 | -11 баллов | Не изменяются | +11баллов |
| Определенные интегралы №2 | -2 балла | Не изменяются | +2 балла |
| Ряды №3 | -4 балла | Не изменяются | +4 балла |
| Комплексные числа №4 | -3 балла | Не изменяются | +3 балла |
Таблица корректировки баллов за все остальное:
| За нахождение ошибок в учебных пособиях | индивидуальные задания |
| За каждую ошибку от 1-5 баллов. Ошибки на запятые, двоеточия и т.п. не принимаются. | За индивидуальные задания по практике и решебникам оценю индивидуально каждого |
Таблица перевода текущих баллов в экзаменационную оценку:
| 0-30 | 31-55 | 56-80 | Свыше 81 |
| неудовлетворительно | удовлетворительно | хорошо | отлично |
III. ЭКЗАМЕН ЗА II СЕМЕСТР ПО МАТЕМАТИКЕ
I. Расписание экзаменов и консультаций (может уточняться!!)
| число | День недели | Аудитория /время | предмет | Вид занятия | ||
| 26.06 | Пятница | 14.00 | математика | Консультация. | 1-7 зачетная неделя/ 8-28 экзамены | |
| 27.06 | Суббота | 9.00 | математика | Экзамен | Менеджмен можно поставить до 5.07 |
II. Список теоретических вопросов к экзамену
ВОПРОСЫ К ЭКЗАМЕНУ ПО ВЫСШЕЙ МАТЕМАТИКЕ
II term
| 1. | Понятие первообразной и неопределённого интеграла. | |
| 2. | Основные свойства неопределённого интеграла. | |
| 3. | Интегралы от основных элементарных функций. | |
| 4. | Основные методы интегрирования Непосредственное интегрирование. | |
| 5. | Основные методы интегрирования Интегрирование методом замены. | |
| 6. | Основные методы интегрирования Интегрирование по частям. | |
| 7. | Правильные и неправильные дроби. | |
| 8. | Разложение рациональных дробей на простейшие дроби. | |
| 9. | Интегрирование простейших рациональных дробей. | |
| Пример интегрирования рациональной дроби. | ||
| 10. | Интегрирование простейших иррациональных дробей вида:  , где , где
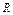 – рациональная функция; – рациональная функция;  – целые числа. – целые числа.
| |
| 11. | Интегрирование простейших иррациональных дробей вида 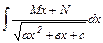
| |
| 12. | Интегрирование тригонометрических функций. Интегралы вида 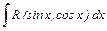 , где , где 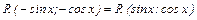 . .
| |
| 13. | Интегрирование тригонометрических функций. Интегралы вида  , где , где  
| |
| 14. | Интегрирование тригонометрических функций. Интегралы вида  , где , где 
| |
| 15. | Интегрирование тригонометрических функций. Интегралы вида  , где , где 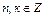
| |
| 16. | Интегрирование тригонометрических функций. Интегралы вида  , ,  , , 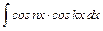
| |
| 17. | Понятие определённого интеграла и его свойства. | |
| 18. | Формула Ньютона-Лейбница. | |
| 19. | Метод разложения для определённого интеграла, примеры. | |
| 20. | Метод подстановки для определённого интеграла, примеры. | |
| 21. | Метод интегрирования по частям для определённого интеграла, примеры. | |
| 22. | Несобственные интегралы I рода: определение, примеры. | |
| 23. | Несобственные интегралы II рода: определение, примеры. | |
| 24. | Понятие числового ряда, его суммы. Необходимое условие сходимости ряда. | |
| 25. | Основные свойства сходящихся рядов. | |
| 26. | Мажорантный и обобщенный признаки сравнения. | |
| 27. | Признаки сходимости Даламбера и Коши. | |
| 28. | Интегральный признак сходимости. | |
| 29. | Знакопеременные ряды. Теорема Лейбница. Оценка остатка ряда. | |
| 30. | Абсолютно сходящиеся ряды, их свойства. | |
| 31. | Функциональные ряды. Основные понятия. Степенной ряд. | |
| 32. | Теорема Абеля. Радиус сходимости степенного ряда. | |
| 33. | Определение комплексных чисел, геометрическая интерпретация , формы записи. | |
| 34. | Действия над комплексными числами: сравнение комплексных чисел, сложение комплексных чисел, вычитание комплексных чкомплексных чисел. | |
| 36. | Действия над комплексными числами: извлечение корня n степени. | |
| 37. | Решение алгебраических уравнений. | |
III. Типовые варианты экзаменационных заданий (проект)
ЭФ ИвГУ,2014-2015 Вариант 1
| ИНТЕГРИРОВАНИЕ Задание 1-5. Найти интегралы, используя различные методы интегрирования. | ||||
| Задание 1 | Задание 2 | Задание 3 | Задание 4 | Задание 5 |

| 
| 
| 
| 
|
КОМПЛЕКСНЫЕ ЧИСЛА
Задание 6. Даны два уравнения  , ,  . Найти все корни уравнений и изобразить их в виде векторов. . Найти все корни уравнений и изобразить их в виде векторов.
| ||||
РЯДЫ
Задание 7. Найти область сходимости степенного ряда  . .
|
ЭФ ИвГУ,2014-2015 Вариант 2
| ИНТЕГРИРОВАНИЕ Задание 1-5. Найти интегралы, используя различные методы интегрирования. | ||||

| 
| 
| 
| 
|
КОМПЛЕКСНЫЕ ЧИСЛА
Задание 6. Дано комплексное число  , ,  .
1) Записать число .
1) Записать число  в алгебраической, тригонометрической и показательной формах.
2) Возвести число в алгебраической, тригонометрической и показательной формах.
2) Возвести число  в указанную степень в указанную степень  . Ответ записать в алгебраической форме.
РЯДЫ
Задание 7. Исследовать сходимость ряда . Ответ записать в алгебраической форме.
РЯДЫ
Задание 7. Исследовать сходимость ряда  по признаку Даламбера по признаку Даламбера  . .
|
IV. На экзамен надо принести: