Вычисление константы равновесия

 

Константу равновесия K_p можно определить экспериментально по значениям парциальных давлений или концентраций. Так как K_p требуется знать в широком диапазоне температур, то возникают существенные трудности в определении парциальных давлений или концентраций. Хотя существует метод «замораживания» химической реакции, когда газовую смесь в состоянии химического равновесия резко охлаждают, и реакции часто практически прекращаются, этот метод не дает результата в случае протекания химических реакций, не требующих высоких температур.

Поэтому основным методом определения K_p является расчетный метод, суть которого состоит в расчете K_p через L^*_max по формуле:

 

L^*_max = – mRT ln K_p.

 

Для расчета L^*_max, как мы знаем, необходимо знать изменение DF (для изохорно-изотермических) и DF (для изобарно-изотермических реакций). Например, для случая (p,T) = const

 

L^*_max = F₁ – F₂ = I₁ – I₂ – T(S₁ – S₂) = – Q _p – T(S₁ – S₂),

 

где S₁ и S₂ – суммарные значения энтропии при температуре T соответственно для исходных веществ и продуктов реакции.

Q _p измерены для различных реакций, и данные доступны.

Энтропии можно представить в виде:

 

S₁ = f₁(p, T) + S_1,0;

S₂ = f₂(p, T) + S_2,0,

 

где S_1,0 и S_2,0 – энтропии при 0°K.

Известно, что

 

dq = T ds и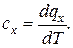

отсюда

 

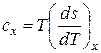и .

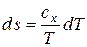Тогда

 

 

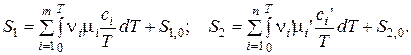
где n_i и n_i’ – стехиометрические коэффициенты уравнения реакции.

Подсчитать энтропии можно, если известна зависимость теплоемкостей от температуры. Кроме того, надо знать константы интегрирования S_1,0 и S_2,0.

Заслуга немецкого химика В. Нернста заключается в том, что он выдвинул предположение, которое потом было подтверждено практикой, получившее название теплового закона Нернста, позволяющее вычислить абсолютные значения энтропий веществ. Он пришел к выводу, чтовблизи абсолютного нуля температуры энтропии всех веществ, находящихся в равновесных состояниях, становятся неизменными и равными между собой, то есть S_1,0 = S_2,0 и с = 0.

В дальнейшем М. Планк доказал, что не только S_1,0 = S_2,0, но и то, что они равны 0.

Интеграл должен вычисляться применительно к конкретному процессу x = const, например, изобарному. При этом надо использовать известную зависимость с_x = с_p = f(T).

В общем случае в процессе изобарного нагревания будут происходить фазовые переходы, поэтому уравнение для абсолютного значения удельной энтропии принимает следующий вид:

 

 

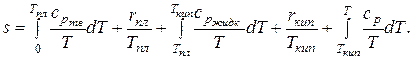
Вычислить это выражение весьма не просто, так как необходимо знать зависимости теплоемкости вещества от температуры в различных фазовых состояниях. В химических справочниках можно найти значения абсолютной энтропии веществ при стандартных условиях (p = 760 мм рт.ст., t = 25 °C). Эта величина обозначается .

Из уравнения

F₁ – F₂ = –mRT ln K_p

 

 

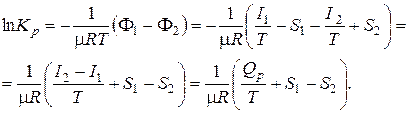
Учитывая связь между натуральным и десятичным логарифмами и значение универсальной газовой постоянной, получим:

 

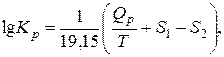
где

 

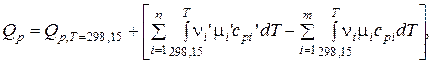
где m – число исходных веществ;

n – число продуктов реакции;

n – cтехиометрические коэффициенты;

' – относится к продуктам реакции.

Для изохорно-изотермической реакции формулы аналогичны, только надо подставлять Q_V и с_V.

Из закона Нернста следует, что

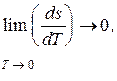
а так как

dq =Tds и ,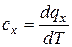

то можно записать

,

следовательно, c_x® 0 и dq ® 0 , то есть теплообмен вблизи абсолютного нуля невозможен. Отсюда следует, что невозможно охладить вещество до температуры абсолютного нуля путем отвода тепла. Абсолютный нуль температуры недостижим.