ТЕОРЕМЫ ЛАПЛАСА.

Формула Бернулли.Производятся испытания, в каждом из которых может появиться со­бытие А или событие `А. Если вероятность события А в одном испы­тании не зависит от появления его в любом другом испытании , то испытания назы­ваются независимыми относительно события А. Будем считать, что ис­пытания происходят в одинаковых условиях и вероятность появления события А в каждом испытании одна и та же. Обозначим эту вероят­ность через p, а вероятность появления события Ā через q (q = 1 -p).

Вероятность того, что в серии из п независимых испытаний событие А появится ровно к раз (и не появится п-k раз), обозначим через Р_n (k), тогда

P_n(k)= , (6.1.)

 

где

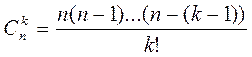
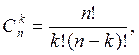
(6.2.)

Формула (6.1.)называется формулой Бернулли.

Число k_о, которому при заданном п соответствует максимальная би­номиальная вероятность Р_n(к_о), называется наивероятнейшем числом появления события А. При заданных п и p это число определяется нера­венствами np-q≤k₀≤np+p (6.3)

Если число пр + р не является целым, то kо равно целой части этого числа (к₀ = [пр + р]); если же пр + р - целое число, то kо имеет два зна­чения k'₀=np-q, k"=np + p.

Вероятность того, что в п испытаниях событие А наступит: а) менее к раз; б) более к раз; в) не менее к раз; г) не более к раз, находят соответ­ственно по формулам: а)P(A)=P_n(o)+P_n(1)+……+P_n(k-1) (6.4)

б)P(A)=P_n(k+1)+P_n(k+2)+……+P_n(n) (6.5)

в)P(A)=P_n(k)+P_n(k+1)+……+P_n(n) (6.6)

г)P(A)=P_n(0)+P_n(1)+……+P_n(k) (6.7)

Распределение Пуассона.В одинаковых условиях производится п независимых испытаний, в каждом из которых может появиться событие А с вероятностью р или событие Āс вероятностью q (q= 1- p). Вероятность того, что при п испытаниях событие А появится к раз (и не появится п – k раз) определя­ется формулой Бернулли (см. формулу (6.1)).

Рассмотрим случай, когда п является достаточно большим, а р - дос­таточно малым; положим пр = а, где а - некоторое число.

Распределением Пуассона называется распределение вероятностей дискретной случайной величины, определяемое формулой Пуассона

(6.8)

 

 

Постоянную a=np (6.9)

входящую в формулу (6.1), называют параметром распределения Пуассона.

Закон распределения Пуассона можно записать в виде следующей таблицы:

X	0	1	2	….	K	….
P	e-a	ae-a		….		….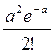

Локальная теорема Лапласа.Если вероятность появления события А в каждом из п независимых испытаний равна одной и той же постоянной р (0 < р < 1), то веро­ятность P_п(к) того, что во всех этих испытаниях событие А поя­вится ровно к раз, приближенно выражается формулой

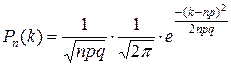, (6.10)

или

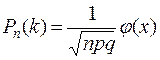, (6.11)

при

, (6.12)

 

 

где

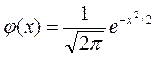(6.13)

 

Отметим, что таблицы значений функции (6.13) даны в приложениях к учебникам и учебным пособиям по теории вероятностей; имеются они и в данном справочном пособии.

Интегральная теорема Лапласа.Если вероятность появления события А в каждом из п независимых испытаний равна одной и той же постоянной р (0 < р < 1), то вероятность P_n(k_1, k₂) того, что во всех этих испытаниях событие А появится не менее k₁ раз и не более k₂ раз, приближенно определяет­ся формулой

, (6.14)

где

(6.15)

 

Эту формулу можно представить в другом виде:

P_n(k₁,k₂)=Ф(x₂)-Ф(x₁) (6.16)

где Ф(х) – функция Лапласа, т.е.

(6.17)

а х₁, и х₂ определяются равенствами (6.15).

Вероятность отклонения относительной частоты от постоянной вероятности в независимых испытаниях.Вероятность того, что при п независимых испытаниях, в каждом из которых вероятность появления события равна р (0<р<1), модуль отклонения частоты появления события от вероятности события не пре­вышает положительного числа ε, приближенно равна удвоенному значе­нию функции Лапласа при

(6.23)

Пример 1.Доля изделий высшего сорта на данном предприятии со­ставляет 30 %. Чему равно наивероятнейшее число изделий высшего сорта в случайно отобранной партии из 75 изделий.

Решение.По условию n = 75, p = 0,3, поэтому q = 1- р=0,7. Со­ставляем двойное неравенство (6.5): 75 • 0,3 - 0,7 ≤ k₀ < 75 • 0,3 + 0,3;

21,8 ≤ k₀ < 22,8.

Отсюда следует, что k₀ = 22 (k₀ = [22,8]).

Ответ :22

Пример 2. Монета подброшена 10 раз. Найти вероятность того, что герб выпадет: а) от 4 до 6 раз; б) хотя бы один раз.

Решение.а)По формуле (6.6) при п = 10, к₁ = 4, к₂= 6, р = q = 0,5 на­ходим

б) Согласно формуле (6.7) получим .

Ответ : а)21/32; б) 1023/1024.

Пример 3.Производятся независимые испытания, в каждом из которых событие А может появиться с вероятностью, равной 0,001. Ка­кова вероятность того, что при 2000 испытаниях событие А появится не менее двух и не более четырех раз.

Решение:Из условия задачи следует, что п = 2000, р = 0,001, а = пр = 2000 • 0,001 = 2, 2 < к < 4. Следовательно

Ответ: 0,541.

Пример 4. Вероятность появления события А в каждом из 900 неза­висимых испытаний равна р = 0,8. Найти вероятность того, что событие

А произойдет не менее 710 раз и не более 740 раз.

Решение. По условию п = 900, к₁ = 710, к₂ = 740, р = 0,8, поэтому

q = 0,2. Согласно формулам (6.20) находим

 

 

По таблице значений функции Лапласа (см. приложение), учитывая нечетность функции, определяем

, .

В соответствии с формулой (4.21) получаем искомую вероятность

P₉₀₀(710,740)=Ф(x₂)-Ф(x₁)=Ф(1,67)-Ф(-0,83)=0,4525-(-0,2967)=0,7492.

Ответ: 0,7492.