КЛАССИФИКАЦИЯ СОБЫТИЙ. КЛАССИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ. СТАТИСТИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ. СВОЙСТВА ВЕРОЯТНОСТИ.

Под вероятностью, в широком смысле, понимают количественную меру неопределенности. Это – число, которое выражает степень уверенности наступления того или иного случайного события.

Случайным называется событие, которое может произойти или не произойти в результате некоторого испытания. В дальнейшем для простоты мы будем опускать термин «случайный».

Мы определим испытание (опыт, эксперимент) как процесс, включающий определенные условия, которые приводят к одному из нескольких возможных исходов. Исходом опыта может быть результат наблюдения или измерения. Единичный, отдельный исход испытания называется элементарным событием.

Достоверное событие – это событие, которое обязательно произойдет в результате испытания. Например, если в урне содержатся только белые шары, то извлечение из нее белого шара есть событие достоверное.Другой пример, если мы подбросим вверх камень, то он обязательно упадет на Землю в силу действия закона притяжения, то есть результат этого опыта заведомо известен. Достоверные события условимся обозначать символом W.

Невозможное событие – это событие , которое не может произойти в результате данного опыта (испытания). Извлечение черного шара из урны с белыми шарами есть событие невозможное событие. Невозможное событие обозначим Æ.

Совместные события. Несколько событий, называются совместными, если в результате эксперимента наступление одного из них не исключает появление других. Например, в магазин вошел покупатель. События «в магазин вошел покупатель старше 60 лет» и «в магазин вошла женщина» - совместные, так как в магазин может войти женщина старше 60 лет.

Несовместные события. Несколько событий называются единственно возможными, если в результате испытания хотя бы одно из них обязательно произойдет (или одно, или два, или все события из рассматриваемой совокупности событий произойдут; одно точно произойдет).

Равновозможные события. Несколько событий называются равновозможными, если в результате испытания ни одно из них не имеет объективно большую возможность появления, чем другие. При бросании игральной кости появление каждой из ее граней – события равновозможные.

Противоположные события. Два единственно возможных события называются противоположными : если А – событие, то - противоположное ему событие. Купля и продажа определенного вида товара есть события противоположные.

Полная группа событий. Совокупность всех единственно возможных и несовместных событий называется полной группой событий.

Вероятностью появления события А называют отношение числа исходов, благоприятствующих наступлению этого события, к общему числу всех единственно возможных и несовместных элементов исходов.

Обозначим число благоприятствующих событию А исходов через М, а число всех исходов через N ,тогда

(2.1)

где М – целое неотрицательное число, 0£ М£ N

Другой тип объективной вероятности определяется исходя из относительной частоты (частости) проявления события. Если, к примеру, некоторая фирма в течении времени провела опрос 1000 покупателей нового сорта напитка и 20 из них оценили его как вкусный, то мы можем оценить вероятность того, что потребителям понравится новый напиток как 20/1000=0,02. В этом примере 20- это частота наступления события, а 20/1000=0,02 – это относительная частота.

Относительной частотой события называется отношение числа

испытаний т, при которых событие появилось, к общему числу проведенных испытаний п. 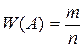, (2.2)

где т – целое неотрицательное число, 0£ т£ п

Статистической вероятностью называется относительная частота (частость) этого события А, вычисленная по результатам большого числа испытаний. Будем обозначать ее : 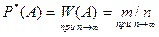. При очень большом числе испытаний статистическая вероятность приближенно равна классической вероятности, т.е. .

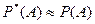Свойства вероятности, вытекающие из классического определения.

1. Вероятность достоверного события рана 1.

2. Вероятность невозможного события равна 0.

3. Вероятность случайного события есть положительное число, заключенное между 0 и 1.

4. Сумма вероятностей противоположных событий равна 1, то есть 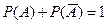или p+q=1,гдеp–вероятность события А , q–вероятность противоположного ему события.

Пример 1. Магазин в целях рекламы нового товара проводит лотерею, в которой 1 главный приз, 5 вторых призов, 100 третьих призов и 1000 четвертых призов. В конце рекламного дня выяснилось, что лотерейные билеты получили 10000 покупателей. По правилам розыгрыша, после извлечения выигрышного билета он не возвращается в урну, и покупатель не может получить более одного выигрыша. Чему равна вероятность того, что покупатель, который приобрел рекламируемый товар: а) выиграет первый приз; б) выиграет любой приз; в) не выиграет ни одного приза?

Решение. Определим событие А: «Покупатель выиграет первый приз». Согласно условию задачи в лотерее участвовало 10000 покупателей, отсюда общее число испытаний N= 10000, а число исходов, благоприятствующих событию А, М=1. Все исходы являются равновозможными, единственно возможными и несовместными элементарными событиями. Следовательно, по формуле классической вероятности:

Соответственно, определим событие В: «Покупатель выиграл любой приз». Для этого события число благоприятствующих исходов М=1+5+100+1000=1106.

Событие «Покупатель не выиграет ни одного приза» - противоположное событию В: «Покупатель выиграл любой приз», поэтому обозначим его как `В. По формуле найдем:

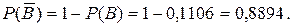
Ответ: а)0,0001; б )0,1106; в)0,8894.

Пример 2.Структура сотрудников в региональном отделении банка имеет следующий вид:

	Женщины	Мужчины
Администрация Операторы

Какова вероятность, что наудачу выбранный сотрудник окажется : а ) мужчина - администратор б) женщина – оператор в)Мужчина г) оператор ?

Решение. а) В банке работают 100 человек, N=100. Из них 15 – мужчин – администраторов , M =15.Следовательно, Р(мужчина-администратор) =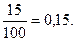

б) 35 сотрудников в банке – женщины – оператор. Следовательно, Р(женщина – оператор) =

в)40 сотрудников в банке – мужчины. Следовательно, Р(мужчина) =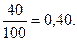

г) Из общего числа служащих в банке 60 – операторы, Следовательно,

Р(оператор) =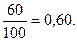

Ответ. а) 0,15 ; б) 0,35 ; в) 0,4; г) 0,6