Объяснить метод определения момента инерции с помощью физического маятника.

Как формируются понятия инерции материальной точки и твердого тела?

Моментом инерции материальной точки относительно неподвижной оси вращения называется физическая величина I, равная произведению массы m материальной точки на квадрат расстояния r² до оси:

I = m r²

Момент инерции твёрдого тела относительно неподвижной оси вращения, складывается из моментов инерции отдельных его материальных точек:

I =Σ mi ri².

В каких ситуациях применима теорема Штейнера?

Если известен момент инерции тела относительно любой оси проходящей через центр масс, то момент инерции относительно любой другой параллельной оси определяется теоремой Штейнера.

Как формируется теорема Штейнера?

Момент инерции I относительно произвольной оси равен сумме момента инерции I0 относительно оси, параллельной данной и проходящей через центр масс тела и произведения массы тела m на квадрат расстояния l между осями:

I = I0 + m l².

Под действием какой силы совершается колебательное движение маятника?

Под действием составляющей силы тяжести P1 = Psinφ .

Является ли момент инерции аддитивной величиной?

Является. Так как к аддитивным величинам относятся масса, энергия, импульс, момент импульса, объем, момент энергии.

Объяснить метод определения момента инерции с помощью физического маятника.

По основному закону динамики вращательного движения:

M = I∙β = - m∙g∙l∙φ (для малых углов отклонения); так как β = d²φ/dt², то получаем дифференциальное уравнение гармонических колебаний:

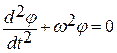, где 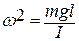; период колебаний

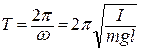; отсюда получаем выражение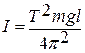

Зная ускорение свободного падения g, массу m, экспериментально измерив l и определив Т, тогда можно вычислить момент инерции маятника 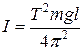.