Уравнение

или 
называется каноническим уравнением гиперболического типа; уравнение

– каноническим уравнением параболического типа; уравнение

– каноническим уравнением эллиптического вида.
Дифференциальное уравнение:
 (1.11)
(1.11)
называется уравнением характеристик.
При решении задач можно воспользоваться представлением уравнения (1.11) в виде системы двух уравнений:
 (1.12)
(1.12)
Для приведения дифференциального уравнения к каноническому виду необходимо записать уравнение характеристик и найти его общие решения.
Для уравнения гиперболического типа уравнение характеристик имеет два интеграла:  ;
;  , т.е. существует два семейства действительных характеристик. С помощью замены переменных
, т.е. существует два семейства действительных характеристик. С помощью замены переменных  ,
,  дифференциальное уравнение приводится к каноническому виду.
дифференциальное уравнение приводится к каноническому виду.
Для уравнения параболического типа оба семейства характеристик совпадают, т.е. уравнение характеристик дает лишь один интеграл  .
.
В этом случае нужно произвести замену переменных  ,
,  , где
, где  – любая функция, удовлетворяющая условию
– любая функция, удовлетворяющая условию  или
или  (например,
(например,  или
или  ). После такой замены уравнение приводится к каноническому виду.
). После такой замены уравнение приводится к каноническому виду.
Для уравнения эллиптического типа интегралы уравнения характеристик имеют вид  , где
, где  и
и  – действительные функции. С помощью подстановки
– действительные функции. С помощью подстановки  ,
,  уравнение приводится к каноническому виду.
уравнение приводится к каноническому виду.
Пример. Определить тип уравнения и привести его к каноническому виду:
 . (1.12)
. (1.12)
Определяем коэффициенты при старших производных в уравнении (1.12):  ,
,  ,
,  . Определяем дискриминант уравнения:
. Определяем дискриминант уравнения:
 . (1.13)
. (1.13)
Т.е. уравнение (1.12) относится к уравнениям эллиптического типа.
Для (1.12) составляем уравнение характеристик:
 (1.14)
(1.14)
и находим его корни:
 ,
,
 . (1.15)
. (1.15)
В результате решение дифференциального уравнения (1.14) получили два комплексно сопряженных корня вида (1.15). Производим замену переменных:
 (1.16)
(1.16)
На следующем этапе выражаем все производные уравнения (1.12) через новые переменные  и
и  для чего необходимо воспользоваться правилом дифференцирования сложной функции нескольких переменных:
для чего необходимо воспользоваться правилом дифференцирования сложной функции нескольких переменных:

Здесь производные от функций  и
и  по переменным
по переменным 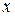 и
и  вычисляются исходя из равенств (1.16).
вычисляются исходя из равенств (1.16).
На последнем этапе решения задачи подставляем полученные значения частных производных в исходное уравнение (1.12), учитывая соответствующие коэффициенты:
 .
.
После преобразования последнего равенства получаем ответ:
 (1.17)
(1.17)
Для упрощения вычислений при решении подобных задач целесообразно пользоваться формулами для выражения частных производных через новые переменные, полученные в общем виде:





При использовании этих уравнений частные производные функций  и
и  по переменным
по переменным 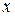 и
и  вычисляются путем подстановки в данные выражения значений
вычисляются путем подстановки в данные выражения значений  и
и  , полученных при решении соответствующего уравнения характеристик. Частные производные функции
, полученных при решении соответствующего уравнения характеристик. Частные производные функции 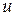 по переменным
по переменным  и
и  не вычисляются.
не вычисляются.