Дифференциальные уравнения с частными производными
Дифференциальное уравнение первого порядка вида 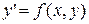 имеет бесчисленное множество решений, определяемых формулой, содержащей одну произвольную постоянную:
имеет бесчисленное множество решений, определяемых формулой, содержащей одну произвольную постоянную: 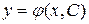 . Аналогично общее решение дифференциального уравнения второго порядка
. Аналогично общее решение дифференциального уравнения второго порядка 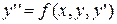 содержит две произвольные постоянные:
содержит две произвольные постоянные: 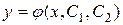 . Выделение частного решения может быть произведено путем задания начальных условий, которые для уравнения второго порядка имеют вид:
. Выделение частного решения может быть произведено путем задания начальных условий, которые для уравнения второго порядка имеют вид: 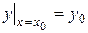 ,
, 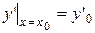 .
.
Подставляя эти значения 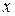 ,
,  и
и 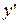 в общее решение и в его производную, получим два уравнения для отыскания произвольных постоянных
в общее решение и в его производную, получим два уравнения для отыскания произвольных постоянных 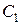 и
и 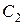 . Если правая часть уравнения – функция
. Если правая часть уравнения – функция 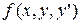 – непрерывна в некоторой окрестности значений
– непрерывна в некоторой окрестности значений 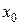 ,
, 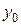 и
и 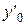 и имеет там непрерывные частные производные
и имеет там непрерывные частные производные  и
и 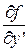 , то существует единственное частное решение, удовлетворяющее данным начальным условиям (теорема существования и единственности решения).
, то существует единственное частное решение, удовлетворяющее данным начальным условиям (теорема существования и единственности решения).
Для однородного уравнения 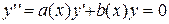 общее решение есть линейная комбинация двух его частных решений
общее решение есть линейная комбинация двух его частных решений  и
и 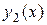 , если только эти решения линейно независимы (т.е.
, если только эти решения линейно независимы (т.е. 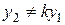 , где
, где  – константа):
– константа):
 . (1.1)
. (1.1)
Общее решение неоднородного уравнения 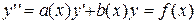 есть сумма какого-либо его частного решения и общего решения соответствующего однородного уравнения.
есть сумма какого-либо его частного решения и общего решения соответствующего однородного уравнения.
Дифференциальные уравнения с частными производными – уравнения, содержащие неизвестную функцию нескольких переменных и ее частные производные. Обычно имеем дело с уравнениями для функций двух или трех независимых переменных. Вот примеры таких уравнений ( 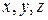 – независимые переменные,
– независимые переменные, 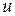 – неизвестная функция):
– неизвестная функция):
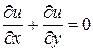 ,
,  ,
,
 ,
, 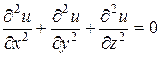 .
.
Порядком дифференциального уравнения называется наивысший порядок входящих в уравнение частных производных. В первой строке написаны уравнения, содержащие частные производные только первого порядка. Такие уравнения называются уравнениями первого рода. Соответственно уравнения, написанные во второй строке, являются примерами уравнений второго рода.
Пусть имеем дифференциальное уравнение с частными производными порядка 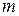 :
:
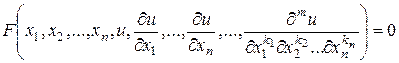 , (1.2)
, (1.2)
связывающее независимые переменные  ,
, 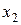 ,…,
,…, 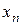 , искомую функцию
, искомую функцию 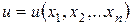 и ее частные производные (наличие хотя бы одной производной обязательно). Здесь
и ее частные производные (наличие хотя бы одной производной обязательно). Здесь 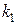 ,
, 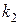 ,…,
,…, 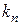 – неотрицательные числа, такие, что
– неотрицательные числа, такие, что  .
.
Обозначим через  множество функций, непрерывных в области
множество функций, непрерывных в области 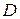 вместе со всеми производными до порядка
вместе со всеми производными до порядка 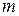 включительно.
включительно.
Определение. Решением дифференциального уравнения (1.2) в некоторой области 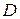 изменения независимых переменных
изменения независимых переменных  ,
, 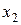 ,…,
,…, 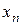 называется всякая функция
называется всякая функция 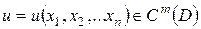 такая, что подстановка этой функции и ее производных в уравнение (1.2) обращает последнее в тождество по
такая, что подстановка этой функции и ее производных в уравнение (1.2) обращает последнее в тождество по  ,
, 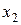 ,…,
,…, 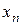 в области
в области 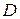 .
.
Рассмотрим несколько примеров: будем считать, что неизвестная функция 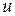 зависит от двух переменных
зависит от двух переменных 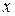 и
и  .
.
Рассмотрим уравнение
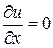 . (1.3)
. (1.3)
Ясно, что искомая функция  не зависит от переменной
не зависит от переменной 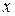 , но может быть любой функцией от
, но может быть любой функцией от  :
:
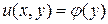 . (1.4)
. (1.4)
Дифференцируя функцию 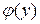 по
по 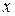 , получаем нуль, а это и значит, что равенство (1.3) соблюдается. Следовательно, решение (1.4) уравнения (1.3) содержит одну произвольную функцию
, получаем нуль, а это и значит, что равенство (1.3) соблюдается. Следовательно, решение (1.4) уравнения (1.3) содержит одну произвольную функцию 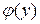 .
.
В этом и заключается коренное отличие решения уравнения с частными производными первого порядка от общего решения обыкновенного дифференциального уравнения первого порядка, которое содержит лишь произвольную постоянную. По аналогии решение (1.4), содержащее одну произвольную функцию, будем называть общим решением уравнения (1.3).
Рассмотрим более сложное уравнение:
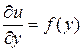 , (1.5)
, (1.5)
где  – заданная функция. Все функции
– заданная функция. Все функции  , удовлетворяющие уравнению (1.5) имеют вид:
, удовлетворяющие уравнению (1.5) имеют вид:
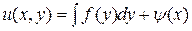 , (1.6)
, (1.6)
где  – произвольная функция от
– произвольная функция от 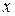 . Это можно проверить, дифференцируя обе части равенства (1.5) по
. Это можно проверить, дифференцируя обе части равенства (1.5) по  :
:
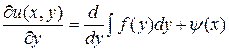 ,
,
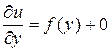 .
.
Найденное решение уравнения (1.5) зависит от одной произвольной функции, т.е. является общим.
Видно, что уравнения с частными производными имеют целые семейства решений. Однако существуют уравнения с частными производными, множества решений которых весьма узки и, в некоторых случаях, даже пусты.
Например, множество действительных решений уравнения: 
исчерпывается функцией  , а уравнение:
, а уравнение: 
вовсе не имеет действительных решений.
Проверим, что уравнение 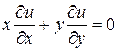 имеет общее решение
имеет общее решение  , где
, где 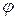 – произвольная дифференцируемая функция.
– произвольная дифференцируемая функция.
Вспомним для этого правило дифференцирования сложной функции нескольких переменных. Если 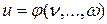 , где
, где 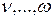 – функции нескольких переменных
– функции нескольких переменных 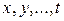 , то
, то 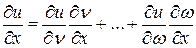 .
.
Аналогичные формулы имеют место и для производных по 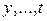 . При этом число промежуточных аргументов
. При этом число промежуточных аргументов 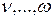 , так же как и число независимых переменных
, так же как и число независимых переменных 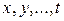 , может быть любым.
, может быть любым.
В данном примере  , где
, где  . Поэтому:
. Поэтому:
 ,
,  .
.
Подставляя эти выражения в уравнение, получим тождество:
 .
.
Рассмотрим теперь уравнение второго порядка:
 . (1.7)
. (1.7)
Положим  . Тогда уравнение (1.7) примет вид
. Тогда уравнение (1.7) примет вид  . Общим решением уравнения
. Общим решением уравнения  будет произвольная функция
будет произвольная функция  . Возвращаясь к функции
. Возвращаясь к функции 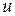 , получим опять уравнение первого порядка:
, получим опять уравнение первого порядка: 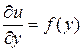 .
.
Согласно (1.6) его общим решением будет функция:
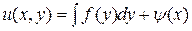 .
.
Так как  – произвольная функция от
– произвольная функция от  , то и интеграл от нее также является произвольной функцией, которую обозначим через
, то и интеграл от нее также является произвольной функцией, которую обозначим через 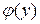 . В результате получили решение в виде:
. В результате получили решение в виде:
 , (1.8)
, (1.8)
где 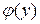 и
и  – произвольные дифференцируемые функции. Легко проверить, что функция (1.8) действительно удовлетворяет уравнению (1.7):
– произвольные дифференцируемые функции. Легко проверить, что функция (1.8) действительно удовлетворяет уравнению (1.7):
 ;
;  .
.
Решение (1.8) уравнения (1.7) с частными производными второго порядка содержит уже две произвольные функции. В этом случае оно называется общим решением.
Проверим, что функция  является общим решением уравнения
является общим решением уравнения  .
.
Согласно правилу дифференцирования сложной функции и обозначая  , последовательно получим:
, последовательно получим:
 ;
;  ;
;
 ;
;  ;
;
 .
.
Подставляя выражения для производных в левую часть уравнения, убеждаемся, что она обращается в нуль:

Таким образом, дифференциальные уравнения математической физики имеют между собой много общих черт: все они – второго порядка и линейны относительно неизвестной функции и ее частных производных. Чаще всего все коэффициенты перед функцией и ее производными – постоянные числа. Общий вид таких уравнений для функции 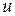 , зависящей от двух переменных
, зависящей от двух переменных 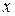 и
и  таков:
таков:
 , (1.9)
, (1.9)
где  ,
,  ,
,  ,
, 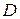 ,
,  ,
,  – постоянные числа, а правая часть – заданная функция переменных
– постоянные числа, а правая часть – заданная функция переменных 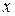 и
и  .
.
Существуют различные виды уравнений в зависимости от соотношения между коэффициентами. Рассмотрим некоторые из них.
При  ,
,  ,
,  получается уравнение первого порядка вида
получается уравнение первого порядка вида  – называемое уравнением переноса. На практике в этом уравнении одной из переменных может быть время
– называемое уравнением переноса. На практике в этом уравнении одной из переменных может быть время  . Тогда его называют также эволюционным уравнением.
. Тогда его называют также эволюционным уравнением.
Если хотя бы один из коэффициентов  ,
,  ,
,  отличен от нуля, то (1.9) является уравнением второго порядка. В зависимости от знака дискриминанта
отличен от нуля, то (1.9) является уравнением второго порядка. В зависимости от знака дискриминанта  оно может принадлежать к одному из трех типов: гиперболическому (
оно может принадлежать к одному из трех типов: гиперболическому (  ), параболическому (
), параболическому (  ) или эллиптическому (
) или эллиптическому (  ).
).
Например,определить вид уравнений:
1)  .
.
 ,
,  ,
,  ,
,  . Следовательно, в области
. Следовательно, в области  уравнение гиперболично, в области
уравнение гиперболично, в области  – эллиптично, а в области
– эллиптично, а в области  – параболично.
– параболично.
2)  .
.
 ,
,  ,
,  ,
,  . Следовательно, это уравнение всюду параболического типа.
. Следовательно, это уравнение всюду параболического типа.
3)  .
.
 ,
,  ,
,  ,
,  . Следовательно, это уравнение гиперболического типа.
. Следовательно, это уравнение гиперболического типа.