Тема 3. Двойственность в задачах линейного программирования

Каждой задаче линейного программирования соответствует двойственная задача. При этом первичная задача по отношению к своей двойственной называется прямой. Двойственная задача по отношению к исходной задаче строится по следующим правилам:

1. Если исходная задача ставится на максимум, то двойственная ставится на минимум и наоборот.

2. Число переменных в двойственной задаче равно числу ограничений в исходной (прямой) задаче.

3. Коэффициенты целевой функции исходной задачи становятся правыми частями ограничений двойственной задачи. Правые части ограничений исходной задачи становятся коэффициентами целевой функции двойственной задачи.

4. Если А – матрица коэффициентов исходной задачи, то транспонированная матрица А^T будет матрицей коэффициентов двойственной задачи.

5. В задаче на максимум все ограничения имеют знак ≤ (=), а в задаче на минимум все ограничения имеют знак ≥.

6. Число переменных в двойственной задаче равно числу ограничений в исходной задаче. Каждому ограничению исходной задачи соответствует переменная двойственной задачи. Если ограничение исходной задач имеет знак (≥), то соответствующая переменная двойственной задачи неотрицательна. Если ограничение имеет знак (=), то соответствующая переменная двойственной задачи может принимать положительные и отрицательные значения и наоборот.

Переменные (у₁,у₂,..,у_т) называются двойственными (или объективно обусловленными) оценками.

Связь двойственных задач представлена в таблице:

Прямая задача	Двойственная задача

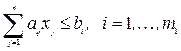
Экономическая интерпретация двойственно обусловленных задач следующая: Вектор х – это вектор выпускаемой продукции, у – двойственные оценки ресурсов прямой задачи (или неявные, теневые цены). Левая часть ограничений двойственной задачи представляет собой оценку затрат на единицу выпускаемой продукции в двойственных ценах.

Прямая задача представляет собой задачу на определение плана, обеспечивающего максимальный выпуск продукции при заданных ценах реализации и ограничениях на ресурсы. Двойственная задача – определение таких оценок ресурсов, в которых стоимость имеющихся ресурсов минимальна, а затраты на производство единицы продукции не меньше цен реализации продукции.

Вопросы для самоконтроля

1. Какая задача ЛП называется двойственной?

2. По каким правилам получается двойственная задача ЛП из основной?

3. Какие двойственные задачи относятся к классу симметричных и несимметричных?

4. Привести примеры двойственных задач, следующих из основных задач ЛП.

Лабораторная работа №3. Определение двойственных оценок. Анализ полученного оптимального плана.

Пример 3.1. В самом начале изучаемого курса (лабораторная работа №1) нами была рассмотрена задача об оптимальном использовании ограниченных ресурсов (о выпуске изделий). Математическая формулировка задачи такова

при ограничениях

Поставим теперь следующий вопрос. Предположим, что некоторая организация желает приобрести дополнительно ресурсы сырья, которым располагает предприятие. В исходной задаче три ограничения по ресурсам: труд, сырье и оборудование. Следовательно, в двойственной задаче – три неизвестных:

у₁ – двойственная оценка ресурса труд, или «цена» единицы трудового ресурса по которой эта организация стала бы покупать указанный ресурс;

у₂ – двойственная оценка ресурса сырье, или «цена» единицы сырья по которой эта организация стала бы покупать это сырье;

у₃ – двойственная оценка ресурса оборудование, или «цена» единицы оборудования.

Необходимо найти такие «цены» на ресурсы , чтобы общая стоимость используемых ресурсов была минимальной.

Выручка от продажи всех ресурсов, расходуемых на изготовление ковра вида А по ценам , составит , ковров вида В соответственно 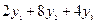, ковров вида С соответственно , ковров вида D соответственно . Предприятие продаст ресурсы, если

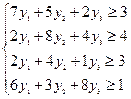
С другой стороны общая стоимость всех запасов ресурсов, составит . Ясно, что организация стремится приобрести ресурсы по возможности дешевле, то есть минимизирует Т(у). Таким образом

Такие задачи линейного программирования, связанные подобного рода особенностями называются взаимно двойственными или сопряженными.

Отметим важные свойства двойственных оценок (из 1-й и 2-й теорем двойственности):

1. если оптимальная оценка i-го ресурса не равна нулю , то в оптимальном плане этот ресурс используется полностью: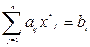

2) если в оптимальном плане ресурс не используется полностью ,

то его оценка равна нулю

3) если j-й продукт входит в оптимальный план 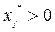, то в оптимальных оценках ресурсов он неубыточен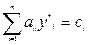

4) если j-й продукт в оптимальных оценках ресурсов убыточен то он не входит в оптимальный план .

Решение двойственной задачи можно найти в отчете Поиска решений – отчете по устойчивости (рис. 3.1).

Проведем анализ полученного оптимального решения исходной задачи с помощью двойственных оценок.

I. Анализ использования ресурсов в оптимальном плане выполняется с помощью соотношений 2-й теоремы двойственности. Ресурсы труд и оборудование имеют отличные от нуля оценки 1,333 и 0,333 – эти ресурсы полностью используются в оптимальном плане, являются дефицитными, сдерживающими рост целевой функции. Правые части этих ограничений равны левым частям:

Ресурс «сырье» используется не полностью:

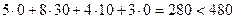
поэтому имеет нулевую двойственную оценку , этот ресурс не влияет на план выпуска продукции и является недефицитным из-за невозможности его полностью использовать в оптимальном плане. Данный ресурс не препятствует и дальше максимизировать целевую функцию исходной задачи функцию L(x).

Рис. 3.1

Общая стоимость используемых ресурсов при выпуске 30 изделий первого вида и 10 изделий третьего вида составит 150 тыс. руб.

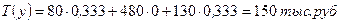
II. Анализ эффективности отдельных вариантов плана выполняется на основе соотношений 2-й теоремы двойственности. Если изделие вошло в оптимальный план (X_j>0), то в двойственных оценках оно не убыточно, т.е. стоимость ресурсов затраченных на производство единицы изделия, равна его цене. Такие изделия эффективны, выгодны с точки зрения принятого критерия оптимальности. В нашей задаче это изделия второго и третьего видов. Если стоимость ресурсов, затраченных на производство одного изделия, больше его цены, то это изделие не войдет в оптимальный план из-за его убыточности. В нашей задаче в план не вошли изделия первого и четвертого видов, потому что затраты по ним превышают цену на 7 (10-3) тыс. руб. и 9,666 (10,666-1) тыс. руб. соответственно. Разницу между правыми и левыми частями ограничений двойственной задачи можно увидеть в Отчете по устойчивости в столбце «Нормируемая стоимость» (Рис.Х). Это также можно подтвердить, подставив в ограничения двойственной задачи оптимальные значения вектора У.

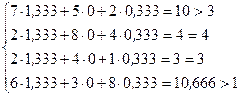
III. Анализ влияния изменения правых частей ограничений на значения целевой функции (чувствительность решения к изменению запасов сырья) выполняется с помощью теоремы об оценках.

Предположим, что запас ресурса «труд» увеличился на 12 ед., т.е. теперь он составляет 80+12=90 ед. Определим изменения значения ЦФ: , т.е. при увеличении ресурса «труд» на 12 ед. значение целевой функции увеличилось на 16 тыс. руб.

Важно знать, до каких пределов могут быть изменены запасы ресурсов? Т.е. интервалы изменения каждого из свободных членов системы ограничений исходной задачи, или интервалы устойчивости двойственных оценок, в которых оптимальный план двойственной задачи не менялся бы. Эту информацию получим из Отчета по устойчивости.

В рассматриваемом примере из фрагмента отчета (рис. 3.2) видно, что запасы дефицитных ресурсов «труд» и «оборудование» могут быть как уменьшены, так и увеличены, в то время как увеличение запаса ресурса «сырье» не повлияют на план выпуска продукции.

Рис. 3.2

Определим, как изменится план выпуска изделий, после увеличения запаса ресурса «труд» до 92 чел./ч. (Рис. 3.3) (решить самостоятельно, экранную форму включить в отчет).

А	B	C	D	E	F	G	H
		Переменные
	Х1	Х2	Х3	Х4
Значение					ЦФ
Коэф. ЦФ
		Ограничения
Вид ресурса					Левая часть	Знак	Правая часть
Труд						<=
Сырье						<=
Оборудование						<=

Рис. 3.3

Из полученного решения видно, что произошло изменение плана выпуска, при этом структура плана не изменилась – изделия первого и четвертого видов были убыточны и они не вошли в новый план, т.к. цены на ресурсы не изменились. Новый план выпуска составляет 28 изделий второго вида и 18 изделий третьего вида. Изменение общей стоимости продукции на 16 тыс. руб. получено за счет уменьшения на 2 ед. изделий второго вида по цене 4 тыс. руб. (4 тыс. руб. *(28-30)= –8 тыс. руб.) и увеличения на 8 ед. изделий третьего вида по цене 3 тыс. руб. (3 тыс. руб.*(18-10)= 24 тыс. руб.), т.о. изменение общей стоимости определяется: 24+(–8)=16.

Новый отчет по устойчивости (рис. 3.4) позволяет провести анализ измененного плана выпуска.

Рис. 3.4

IV. Чувствительность решения к изменению коэффициентов целевой функции исходной задачи.

В первой части Отчета по устойчивости содержится информация о допустимом увеличении и уменьшении коэффициентов целевой функции, при которых не изменяется оптимальный план исходной задачи.

Пример 3.2.Определить являются ли векторы X = (1, 0, 1) и Y = (4,5; −3,5) оптимальными решениями задачи

при ограничениях

и двойственной к ней задаче.

Решение. Проверим X на допустимость

составим двойственную задачу:

при ограничениях:

Проверим Y на допустимость

Таким образом,

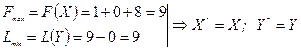
Задачи для самостоятельного решения:

Задача 1. Для изготовления 4 видов продукции используют три вида сырья. Запасы сырья, нормы его расхода и цены реализации единицы каждого вида продукции приведены в таблице.

Тип сырья	Нормы расхода сырья на одно изделие	Запасы сырья
А	Б	В	Г



Цена изделия

Требуется:

1. сформулировать прямую оптимизационную задачу на максимум стоимости выпускаемой продукции, решить её и провести анализ полученных результатов;

2. сформулировать двойственную задачу и найти её оптимальный план;

3. проанализировать использование ресурсов в оптимальном плане;

4. разобрать свойства двойственных оценок;

5. определить, как изменится общая стоимость продукции и план её выпуска при увеличении запасов сырья 1 и 2 вида на 4 и 3 единицы соответственно и уменьшении на 3 единицы сырья 3 вида.;

6. определить целесообразность включения в план производства изделий «Д» ценой 10 единиц, на изготовление которого расходуется по две единицы каждого вида сырья.

Задача 2. Для изготовления 4 видов продукции используют три вида сырья. Запасы сырья, нормы его расхода и цены реализации единицы каждого вида продукции приведены в таблице.

Тип сырья	Нормы расхода сырья на одно изделие	Запасы сырья
А	Б	В	Г



Цена изделия

Требуется:

2. сформулировать двойственную задачу и найти её оптимальный план;

3. проанализировать использование ресурсов в оптимальном плане;

4. разобрать свойства двойственных оценок;

5. определить, как изменится общая стоимость продукции и план её выпуска при увеличении запасов сырья 2 и 3 вида на 120 и 160 единиц соответственно и уменьшении на 60 единиц сырья 1 вида.;

6. определить целесообразность включения в план производства изделий «Д» ценой 12 единиц, на изготовление которого расходуется по две единицы каждого вида сырья.

Задача 3. Для изготовления 4 видов продукции используют три вида сырья. Запасы сырья, нормы его расхода и цены реализации единицы каждого вида продукции приведены в таблице.

Тип сырья	Нормы расхода сырья на одно изделие	Запасы сырья
А	Б	В	Г



Цена изделия

Требуется:

2. сформулировать двойственную задачу и найти её оптимальный план;

3. проанализировать использование ресурсов в оптимальном плане;

4. разобрать свойства двойственных оценок;

Задача 4. Для изготовления 3 видов продукции используют три вида сырья. Запасы сырья, нормы его расхода и цены реализации единицы каждого вида продукции приведены в таблице.

Требуется:

Тип сырья	Нормы расхода сырья на одно изделие	Запасы сырья
А	Б	В



Цена изделия

2. сформулировать двойственную задачу и найти её оптимальный план;

3. проанализировать использование ресурсов в оптимальном плане;

4. разобрать свойства двойственных оценок;

5. определить, как изменится общая стоимость продукции и план её выпуска при увеличении запасов сырья 1 и 3 вида на 4 единицы каждого;

6. определить целесообразность включения в план производства изделий «Г» ценой 13 единиц, на изготовление которого расходуется по 1, 3 и 2 единицы каждого вида сырья соответственно и изделия «Д» ценой 12 единиц, на изготовление которого расходуется по две единицы каждого вида сырья.

Задача 5. На основании информации, приведенной в таблице, решить задачу оптимального использования ресурсов на максимум выручки от реализации готовой продукции.

Тип сырья	Нормы расхода сырья на одно изделие	Запасы сырья

Труд
Сырье
Оборудование
Цена изделия

Требуется:

1. сформулировать прямую оптимизационную задачу на максимум выручки от реализованной продукции, решить её и провести анализ полученных результатов;

2. сформулировать двойственную задачу и найти её оптимальный план;

3. проанализировать использование ресурсов в оптимальном плане;

4. разобрать свойства двойственных оценок;

5. определить, как изменится выручка от реализации продукции и план её выпуска при увеличении запасов сырья на 18 единиц;

6. определить целесообразность включения в план производства изделий четвертого вида ценой 70 единиц, на изготовление которого расходуется по две единицы каждого вида ресурсов.

Задача 6. На основании информации, приведенной в таблице, решить задачу оптимального использования ресурсов на максимум выручки от реализации готовой продукции.

Тип сырья	Нормы расхода сырья на одно изделие	Запасы сырья
А	Б	В



Цена изделия

Требуется:

2. сформулировать двойственную задачу и найти её оптимальный план;

3. проанализировать использование ресурсов в оптимальном плане;

4. разобрать свойства двойственных оценок;

5. определить, как изменится выручка от реализации продукции и план её выпуска, если запас сырья 1 вида увеличить на 45 единиц, а 2 уменьшить на 9 единиц;

6. определить целесообразность включения в план производства изделий «Г» ценой 11 единиц, на изготовление которого расходуется по 9, 4 и 6 единиц каждого вида сырья соответственно.

Задача 7. Предприятие выпускает четыре вида продукции и использует три вида оборудования: токарное, фрезерное и шлифовальное. Общий фонд рабочего времени оборудования каждого вида, нормы расхода и цены реализации единицы каждого вида продукции приведены в таблице.

Тип оборудования	Нормы расхода сырья на одно изделие	Фонд рабочего времени
А	Б	В	Г
Токарное
Фрезерное
Шлифовальное
Цена изделия

Требуется:

2. сформулировать двойственную задачу и найти её оптимальный план;

3. проанализировать использование ресурсов в оптимальном плане;

4. разобрать свойства двойственных оценок;

5. определить, как изменится общая стоимость продукции и план её выпуска, если фонд рабочего времени шлифовального оборудования увеличить на 24 часа.

6. определить целесообразность включения в план производства изделий «Д» ценой 11 единиц, если нормы затрат оборудования 8, 2 и 2 единицы соответственно.

Задача 8. На основании информации, приведенной в таблице, решить задачу оптимального использования ресурсов на максимум выручки от реализации готовой продукции.

Тип сырья	Нормы расхода сырья на одно изделие	Запасы сырья




Цена изделия

Требуется:

2. сформулировать двойственную задачу и найти её оптимальный план;

3. проанализировать использование ресурсов в оптимальном плане;

4. разобрать свойства двойственных оценок;

5. определить, как изменится выручка от реализации продукции и план её выпуска при увеличении запаса сырья 1 вида на 80 единиц, а 2 - уменьшить на 10 единиц;

6. определить целесообразность включения в план производства изделий четвертого вида ценой 7 единиц, если нормы затрат сырья 2, 4 и 3 единицы соответственно.

Задача 9. Для изготовления 4 видов продукции используют три вида сырья. Запасы сырья, нормы его расхода и цены реализации единицы каждого вида продукции приведены в таблице.

Тип сырья	Нормы расхода сырья на одно изделие	Запасы сырья
А	Б	В	Г
			0,5


Цена изделия	7,5

Требуется:

2. сформулировать двойственную задачу и найти её оптимальный план;

3. проанализировать использование ресурсов в оптимальном плане;

4. разобрать свойства двойственных оценок;

5. определить, как изменится общая стоимость продукции и план её выпуска при увеличении запасов сырья 1 вида на 100 единиц и уменьшении на 150 единиц сырья 2 вида;

6. определить целесообразность включения в план производства изделий «Д» ценой 10 единиц, если нормы затрат сырья 2, 4, и 3 единицы.

Задача 10. Для изготовления трех видов продукции используется четыре вида ресурсов. Запасы ресурсов, нормы расхода и цены реализации единицы каждого вида продукции приведены в таблице.

Вид ресурсов	Нормы расхода ресурсов на одно изделие	Запасы ресурсов

Труд
Сырье 1
Сырье 2
Оборудование
Цена изделия

Требуется:

2. сформулировать двойственную задачу и найти её оптимальный план;

3. проанализировать использование ресурсов в оптимальном плане;

4. разобрать свойства двойственных оценок;

5. определить, как изменится общая стоимость продукции и план её выпуска при увеличении запаса сырья 1 вида на 24единицы;

6. определить целесообразность включения в план производства изделий четвертого вида ценой 11 единиц, если нормы затрат сырья 8, 4, 20 и 6 единиц соответственно.