МОМЕНТ ИНЕРЦИИ РАЗЛИЧНЫХ ТЕЛ. ТЕОРЕМА ШТЕЙНЕРА.
Отчет по лабораторной работе №15
Кафедра: Общей технической физики
По дисциплине: Физика
Выполнил: студент гр. ТНГ-10-2 ______________ Щербань А.И.
(подпись) (Ф.И.О.)
Оценка: _____________
Дата: __________________
Проверил: доцент ______________ Немов С.А.
(должность) (подпись) (Ф.И.О.)
Санкт-Петербург
Цель работы: измерение моментов инерции различных тел. Проверка теоремы Штейнера.
Краткое теоретическое содержание:  Момент инерции тела является мерой инертности тела при вращательном движении, подобно тому, как масса тела является мерой инертности тела при поступательном движении. Момент инерции тела зависит от размеров и формы тел и от распределения массы тела относительно оси вращения. Для вычисления момента инерции твердого тела относительно некоторой оси ОО разобьем мысленно тело на большое число весьма малых элементов - материальных точек (рис.1). Тогда момент инерции такой отдельной элементарной массы
Момент инерции тела является мерой инертности тела при вращательном движении, подобно тому, как масса тела является мерой инертности тела при поступательном движении. Момент инерции тела зависит от размеров и формы тел и от распределения массы тела относительно оси вращения. Для вычисления момента инерции твердого тела относительно некоторой оси ОО разобьем мысленно тело на большое число весьма малых элементов - материальных точек (рис.1). Тогда момент инерции такой отдельной элементарной массы
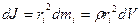
где 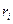 - расстояние от элемента объема
- расстояние от элемента объема 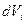 до оси вращения, r - плотность вещества.
до оси вращения, r - плотность вещества.
Момент инерции всего тела
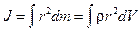 ,
,
Таким образом, момент инерции различных тел можно найти с помощью интегрирования.
Рассмотрим результаты расчета для некоторых частных случаев.
1. Момент инерции материальной точки массой m , находящейся на расстоянии R от оси вращения
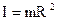 (1)
(1)
2. Момент инерции однородного диска относительно оси, перпендикулярной к плоскости диска и проходящей через его центр. Радиус диска R, его масса m.
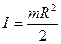 (2)
(2)
.Эта же формула справедлива для момента инерции сплошного цилиндра относительно оси совпадающей с осью цилиндра..
3. Момент инерции полого цилиндра с внутренним радиусом R1 и внешним радиусом R2 относительно оси , совпадающей с осью цилиндра.
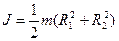 (3)
(3)
4. Момент инерции шара радиуса R относительно оси проходящей через его центр.
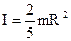 (4)
(4)
5. Момент инерции тонкого стержня относительно оси перпендикулярной к стержню и проходящей через его середину. Длина стержня l,
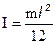 (5)
(5)
Эти формулы для моментов инерции относительно оси симметрии.
Момент инерции относительно произвольной оси можно найти с помощью теоремы Штейнера:
Момент инерции относительно произвольной оси О1О1 равен сумме момента инерции I0, относительно оси OO, параллельной данной и проходящей через центр инерции тела и произведения массы тела на квадрат расстояния d между осями.

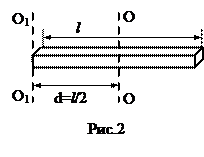 Получим с помощью этой теоремы формулу момента инерции стержня относительно оси перпендикулярной к стержню и проходящей через его конец.
Получим с помощью этой теоремы формулу момента инерции стержня относительно оси перпендикулярной к стержню и проходящей через его конец.
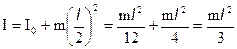 (6)
(6)
В общем случае расчет момента инерции представляет собой достаточно сложную задачу, и часто он определяется экспериментально с помощью основного уравнения динамики вращательного движения, методом крутильных колебаний и др.
В данной работе для экспериментального измерения моментов инерции различных тел используется метод крутильных колебаний.
Исследуемые тела насаживаются на ось спиральной пружины. Если зкрутить пружину на угол j, то в результате деформации пружины возникнет упругая сила. Она создает крутящий момент (момент силы) М
M=Dj (7)
Здесь D – модуль кручения пружины.
Этот крутящий момент стремится вернуть пружину в исходное (равновесное) состояние. В результате возникают крутильные колебания.
Из теории крутильных колебаний следует формула для периода колебаний
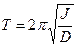 (8)
(8)
где J - момент инерции.
Отсюда
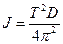 (9)
(9)
Таким образом, измеряя период крутильных колебаний и зная модуль кручения D пружины, можно вычислить момент инерции тела, насаженного на ось пружины.
Определение основных физических понятий, объектов, процессов и величин:
Момент инерции тела – мера инертности тела при вращательном движении;
Момент силы (крутящий момент) – векторная физическая величина, характеризует вращательное действие силы на твердое тело.
Модуль кручения пружины – скалярная физическая величина, равная модулю отношения крутящего момента к углу закручивания пружины.
Пояснения к основным физическим величинам:
M – момент силы [ Н/м];
D – модуль кручения пружины;
l– плечо силы [м];
F – сила, необходимая для удержания стержня в нужном положении [Н];
T – период крутильных колебаний [с];
J – момент инерции тела [кг·  ];
];
r – расстояние от оси вращения до центров грузов [м];
Jст – момент инерции стержня [кг·  ];
];
d – некоторое расстояние [м];
R – радиус тела [м];
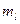 – масса стержня [кг];
– масса стержня [кг];
m – масса[кг].
Основные расчетные формулы:
 ;
;
 ;
;
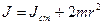 , где
, где 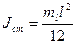 ;
;
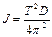 ;
;
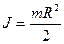 ;
;
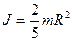 ;
;
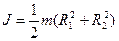 ;
;
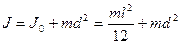 ;
;
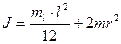 .
.
Формулы расчета погрешностей косвенных измерений:
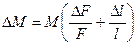 – средняя абсолютная погрешность расчета момента силы;
– средняя абсолютная погрешность расчета момента силы;
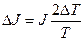 – средняя абсолютная погрешность расчета момента инерции исследуемого тела (экспериментально);
– средняя абсолютная погрешность расчета момента инерции исследуемого тела (экспериментально);
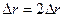 – средняя абсолютная погрешность расчета расстояний от оси вращений до центров грузов;
– средняя абсолютная погрешность расчета расстояний от оси вращений до центров грузов;
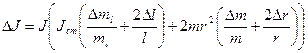 – средняя абсолютная погрешность расчета момента инерции стержня с грузами;
– средняя абсолютная погрешность расчета момента инерции стержня с грузами;
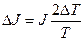 – средняя абсолютная погрешность расчета момента инерции стержня.
– средняя абсолютная погрешность расчета момента инерции стержня.
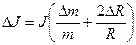 – средняя абсолютная погрешность расчета момента инерции сплошного цилиндра и диска;
– средняя абсолютная погрешность расчета момента инерции сплошного цилиндра и диска;
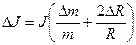 – средняя абсолютная погрешность расчета момента инерции шара;
– средняя абсолютная погрешность расчета момента инерции шара;
 – средняя абсолютная погрешность расчета момента инерции полого цилиндра;
– средняя абсолютная погрешность расчета момента инерции полого цилиндра;
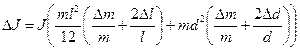 – средняя абсолютная погрешность расчета момента инерции стержня по теореме Штейнера.
– средняя абсолютная погрешность расчета момента инерции стержня по теореме Штейнера.
Ход работы:
1) Для определения модуля кручения D пружины взяла стержень с грузами и насадила его на ось пружины, грузы сдвинула к центру, повернула стержень на заданные углы, измерила силу F с помощью динамометра. Вычислила момент силы M по формуле М=Fl. Полученные данные занесла в таблицу:
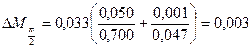 [ Н/м];
[ Н/м]; 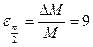 %;
%;
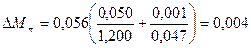 [ Н/м];
[ Н/м]; 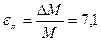 %;
%;
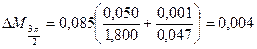 [ Н/м];
[ Н/м];  %;
%;
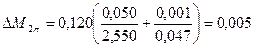 [ Н/м];
[ Н/м]; 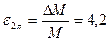 %.
%.
| j | F | l | M |
| p/2 | 0,700±0,050 | 0,047±0,001 | 0,033±0,003 |
| p | 1,200±0.050 | 0,047±0,001 | 0,056±0,004 |
| 3p/2 | 1,800±0,050 | 0,047±0,001 | 0,085±0,004 |
| 2p | 2,550±0,050 | 0,047±0,001 | 0,120±0,005 |
По полученным данным построила график зависимости М от φ:
M
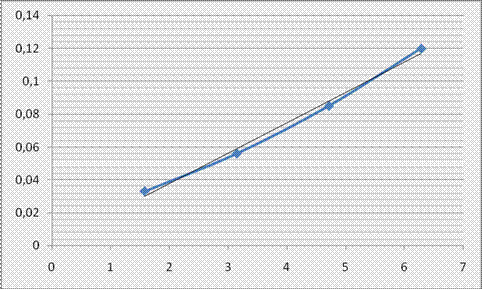
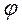
Определила модуль кручения пружины D
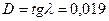 .
.
2) А. Определение моментов инерции различных тел относительно оси, проходящей через центр симметрии.
Насадила на ось пружины исследуемое тело, закрутила пружину на 180º и отпустила, измерила T, проделав несколько опытов. Далее замерила R, m и вычислила момент инерции исследуемого тела (экспериментальный и теоретический).
Результаты занесла в таблицы:
Цилиндр
| 1 | 2 | 3 | 4 | 5 | |
| T[с] | 1,016±0,001 | 1,016±0,001 | 1,016±0,001 | 1,016±0,001 | 1,016±0,001 |
| m[кг] | 0,353±0,001 | 0,353±0,001 | 0,352±0,001 | 0,352±0,001 | 0,353±0,001 |
| R[м] | 0,050±0,001 | 0,050±0,001 | 0,050±0,001 | 0,050±0,001 | 0,050±0,001 |
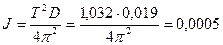 [кг·
[кг·  ];
]; 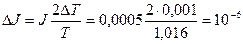 [кг·
[кг·  ];
];
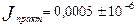 [кг·
[кг·  ];
];  .
.
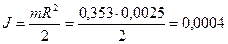 [кг·
[кг·  ];
];
 [кг·
[кг·  ];
];
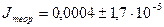 [кг·
[кг·  ];
]; 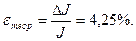
Диск
| 1 | 2 | 3 | 4 | 5 | |
| T[с] | 1,747±0,001 | 1,747±0,001 | 1,748±0,001 | 1,747±0,001 | 1,748±0,001 |
| m[кг] | 0,262±0,001 | 0,262±0,001 | 0,263±0,001 | 0,263±0,001 | 0,262±0,001 |
| R[м] | 0,108±0,001 | 0,108±0,001 | 0,109±0,001 | 0,108±0,001 | 0,108±0,001 |
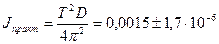 [кг·
[кг·  ];
]; 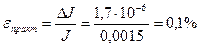 .
.
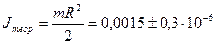 [кг·
[кг·  ];
]; 
Шар
| 1 | 2 | 3 | 4 | 5 | |
| T[с] | 1,675±0,001 | 1,675±0,001 | 1,674±0,001 | 1,675±0,001 | 1,674±0,001 |
| m[кг] | 0,651±0,001 | 0,651±0,001 | 0,652±0,001 | 0,652±0,001 | 0,651±0,001 |
| R[м] | 0,068±0,001 | 0,068±0,001 | 0,067±0,001 | 0,068±0,001 | 0,068±0,001 |
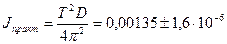 [кг·
[кг·  ];
]; 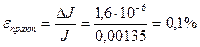 .
.
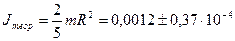 [кг·
[кг·  ];
];  %.
%.
Полый цилиндр
| 1 | 2 | 3 | 4 | 5 | |
| T[с] | 1,313±0,001 | 1,303±0,001 | 1,313±0,001 | 1,313±0,001 | 1,302±0,001 |
| m[кг] | 0,352±0,001 | 0,352±0,001 | 0,353±0,001 | 0,352±0,001 | 0,352±0,001 |
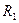 [м] [м]
| 0,051±0,001 | 0,051±0,001 | 0,051±0,001 | 0,051±0,001 | 0,051±0,001 |
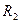 [м] [м]
| 0,047±0,001 | 0,047±0,001 | 0,047±0,001 | 0,048±0,001 | 0,047±0,001 |
 [кг·
[кг·  ];
]; 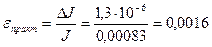 %.
%.
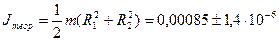 [кг·
[кг·  ];
]; 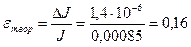 %.
%.
В. Изучение зависимости момента инерции от расстояния масс от оси вращения (m=0,212±0,001[кг]; 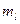 =0,132±0,001[кг]; l=0,600±0,001[м]).
=0,132±0,001[кг]; l=0,600±0,001[м]).
| r, (м) | 0,027±0,001 | 0,047±0,001 | 0,067±0,001 | 0,087±0,001 | 0,107±0,001 | 0,127±0,001 |
| r2, (м2) | 0,073· 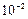 ±0,002 ±0,002
| 0,002±0,002 | 0,004±0,002 | 0,008±0,002 | 0,011±0,002 | 0,016±0,002 |
| T, (с) | 2,950±0,001 | 3,431±0,001 | 4,196±0,001 | 5,101±0,001 | 6,080±0,001 | 7,137±0,001 |
| J, (кг.*м2) | 0,004±0,265 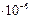
| 0,005±0,410 
| 0,006±0,603 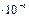
| 0,007±0,951 
| 0,009±0,136 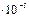
| 0,012±0,217 
|
1)  [кг·
[кг·  ];
];
 [кг·
[кг·  ];
];
 [кг·
[кг·  ];
];  %.
%.
 [кг·
[кг·  ];
];

[кг·  ];
];
 [кг·
[кг·  ];
];  %.
%.
2)  [кг·
[кг·  ];
];  %.
%.
 [кг·
[кг·  ];
];  %.
%.
3)  [кг·
[кг·  ];
];  %.
%.
 [кг·
[кг·  ];
];  %.
%.
4)  [кг·
[кг·  ];
];  %.
%.
 [кг·
[кг·  ];
];  %.
%.
5)  [кг·
[кг·  ];
];  %.
%.
 [кг·
[кг·  ];
];  %.
%.
6)  [кг·
[кг·  ];
];  %.
%.
 [кг·
[кг·  ];
];  %.
%.



 ±0,004·10
±0,004·10  −теоретическое значениемомента инерции стержня;
−теоретическое значениемомента инерции стержня;
Отрезок на оси ординат, равный Jст , так же равен теоретическому значению.