Понятие о выборочном методе
МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Методы сбора, систематизации, обработки и использования эмпирических данных - результатов наблюдений массовых случайных явлений, выявление статистических закономерностей составляют основное содержание математической статистики.
В отличие от теории вероятностей, которая позволяет выявить те или иные свойства случайных событий путем абстрактного, логического анализа, не проводя эксперимента, в математической статистике любое исследование связано с эмпирическими данными и идет от практики к гипотезе и ее проверке.
Методы математической статистики позволяют решать следующие задачи:
- изучение всей совокупности по некоторому числу случайно отобранных объектов или случайно выбранных значений признака (выборочный метод);
- нахождение и сравнение приближенных значений числовых характеристик статистических распределений (статистическое оценивание);
- построение теоретического распределения значений изучаемого признака по эмпирическим данным и проверка его согласия с эмпирическими данными (критерии согласия);
- установление формы и тесноты взаимосвязи между изучаемыми признаками (корреляционный и регрессионный анализ).
Методы математической статистики основываются на возможности вероятностной интерпретации изучаемых совокупностей. Теоретической основой математической статистики является теория вероятностей.
ВЫБОРОЧНЫЙ МЕТОД
Понятие о выборочном методе
Исходным материалом любого статистического исследования является статистическая совокупность. Статистической совокупностью называют подлежащее статистическому изучению множество однородных объектов, объединенных с целью изучения некоторого признака, присущего всем объектам совокупности.
Отдельные объекты этой совокупности называют элементами, или единицами, совокупности, а их число - объемом совокупности. Например, в качестве статистической совокупности можно назвать совокупность студентов академии, элементами здесь являются студенты, рассматриваемые в отдельности, а объемом совокупности - численность студентов; признаками совокупности могут быть возраст студентов, их рост, успеваемость и т.д. Признаки принято обозначать прописными буквами латинского алфавита Х,У, ..., как и случайные величины.
Значения признака при переходе от одного элемента совокупности к другому изменяются, то есть варьируют. Различные значения признака называют вариантами и обозначают соответствующими строчными буквами с индексом.
Признаки могут быть количественными или качественными. Например, количественный признак - рост студентов или их возраст, а качественный - успеваемость (успевает, не успевает).
Статистическое наблюдение, в результате которого получают значения признака, являющиеся элементами совокупности, может быть сплошным или выборочным. При сплошном наблюдении изучается каждый элемент всей исходной совокупности. Однако сплошное наблюдение может оказаться либо просто невозможно или связано с большими материальными и временными затратами, если объем совокупности велик; либо лишено смысла в том случае, если при наблюдении элементы совокупности уничтожаются (например, исследование прочности материала, продолжительности горения электроламп и т.д.). Поэтому на практике используют выборочное наблюдение. Для этого из исходной совокупности, которую принято называть генеральной, случайным образом выбирается ее часть, называемая выборочной совокупностью, или выборкой, все элементы которой подвергаются сплошному наблюдению. Объем генеральной совокупности обозначают N, а объем выборки - n 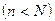 .
.
Чтобы выборка как можно точнее воспроизводила свойства генеральной совокупности, она должна быть репрезентативной (представительной). Из закона больших чисел следует, что выборка будет репрезентативной, если она случайна и все элементы выборки имеют одинаковую вероятность попасть в выборку; имеет достаточно большой объем; однородна по рассеянию значений элементов.
По характеру отбора элементов различают выборки повторные и бесповторные. В повторной выборке элементы после изучения (то есть после определения количественных характеристик признака) возвращаются в генеральную совокупность, в бесповторной - не возвращаются. Если выборка по своему объему составляет незначительную часть генеральной совокупности, что чаще всего и бывает на практике, то сколько-нибудь существенного различия между повторной и бесповторной выборками нет.