Примеры решения задач.

 

Пример №1. Найти изменение DS энтропии при нагревании воды массой m=100 г от температуры t₁=0°C до температуры t₂=100 °С и последующем превращении воды в пар той же температуры.

 

Решение. Найдем отдельно изменение энтропии DS' при нагревании воды и изменение энтропии DS" при превращении ее в пар. Полное изменение энтропии выразится суммой DS' и DS".

Как известно, изменение энтропии выражается общей формулой

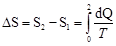(1)

При бесконечно малом изменении dT температуры нагреваемого тела затрачивается количество теплоты 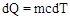, где m — масса тела; с — его удельная теплоемкость. Подставив выражение dQ в равенство (1), найдем формулу для вычисления изменения энтро­пии при нагревании воды:

.

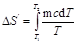Вынесем за знак интеграла постоянные величины и произведем интегрирование, тогда получим

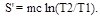
После вычислений найдем 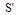=132 Дж/К.

При вычислении по формуле (1) изменения энтропии во время превращения воды в пар той же температуры постоянная температуpa T 'выносится за знак интеграла. Вычислив интеграл, найдем

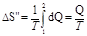(2)

где Q — количество теплоты, переданное при превращении нагре­той воды в пар той же температуры.

Подставив в равенство (2) выражение количества теплоты Q=lm, где l — удельная теплота парообразования, получим

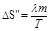(3)

Произведя вычисления по формуле (3), найдем

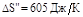
Полное изменение энтропии при нагревании воды и последую­щем превращении ее в пар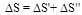

 

Пример №2. Определить изменение DS энтропии при изотермиче­ском расширении кислорода массой m=10 г от объема V₁=25 л до объема V₂=100 л.

 

Решение. Так как процесс изотермический, то в общем выражении энтропии 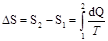температуру выносят за знак интеграла. Выполнив это, получим

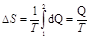(1)

Количество теплоты, полученное газом, найдем по первому началу термодинамики: 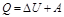. Для изотермического процесса 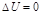. (2)

Работа 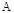для этого процесса определяется по формуле

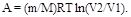(3)

С учетом (2) и (3) равенство (1) примет вид

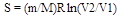. (4)

Подставив в (4) числовые значения и произведя вычисления, по­лучим

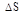=(10×10^-3/(32×10^-3)) ×8,31 ln(100×10^-3/(25×10^-3)) Дж/К=3,60 Дж/К.