ПАРНАЯ ЛИНЕЙНАЯ РЕГРЕССИЯ И КОРРЕЛЯЦИЯ
Цель: рассмотреть вопросы взаимосвязи экономических переменных, суть регрессионного анализа, парной линейной регрессии и корреляции. Для нахождения параметров уравнения линейной регрессии научиться использовать метод наименьших квадратов.
Ключевые слова: корреляционная связь, уравнение парной регрессии, метод наименьших квадратов, коэффициент корреляции.
План лекции:
1. Парная линейная регрессия.
2. Метод наименьших квадратов.
3. Коэффициент корреляции.
1.Парная линейная регрессия.
Различные экономические показатели, как на микро, так и на макроуровне не являются независимыми, а связаны между собой. Например, цена какого - либо товара и величина спроса на этот товар, объем производства и прибыль фирмы, располагаемый доход и объем личного потребления, инфляция и безработица. Задачей регрессионного анализа является установление формы зависимости между переменными.
В естественных науках часто речь идет о функциональной зависимости, когда каждому значению одной переменной соответствует единственное значение другой.
Взаимосвязи экономических показателей редко имеют простой функциональный вид, так как на интересующий нас показатель, оказывают влияние и множество других случайных факторов. В результате чего каждому значению одной переменной может соответствовать множество значений другой переменной. Например, домохозяйства с одинаковым среднемесячным доходом имеют разный объем расходов на продукты питания в месяц. Т.е. под влиянием каких-то неучтенных факторов расставляются приоритеты в потребительской корзине. Связь переменных, на которую воздействуют случайные факторы называется статистическойсвязью. Статистическая зависимость называется корреляционной, если каждому значению одной переменной соответствует определенное условное математическое ожидание (среднее значение) другой.
Пусть требуется оценить связь между переменными Х и У, т.е. нужно найти формулы этой связи. Для решения такой задачи используются статистические данные о динамике этих показателей. Пусть имеется ряд значений показателя Х: х1, х2, …, хn и ряд значений показателя У:у1, у2, …, уn. Построим точки (х1, у1), (х2, у2), ..., (хn, уn) на графике и соединим их линией. Если это реальные статистические данные, то мы никогда не получим простую линию - линейную, квадратичную, экспоненциальную и т.д. Всегда будут присутствовать отклонения зависимой переменной, вызванные ошибками, измерения или влиянием случайных факторов.
Рассмотрим в качестве примера зависимость между прибылью (тыс. тг.) и выработкой продукции на одного человека (ед.) по 12 предприятиям:
| № предприятия | ||||||||||||
| Прибыль, у | ||||||||||||
| Выработка, х |
На рисунке представлено поле корреляции эмпирических значений переменных, которые были аппроксимированы линейным уравнением регрессии:
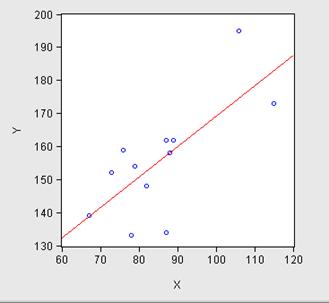
Уравнение регрессии – это формула статистической связи между переменными. Уравнение линейной регрессии имеет вид:
у = а + b·х
Величина у является объясняемой (зависимой) переменной или результирующим признаком, а х - объясняющей (независимой) переменной или факторным признаком. Постоянные а и b называются параметрами уравнения.
В зависимости от количества факторов, включенных в уравнение регрессии, принято различать парную (от двух переменных) и множественную (от нескольких переменных) регрессии.
2.Метод наименьших квадратов.
Для оценки параметров а и b используется метод наименьших квадратов (МНК), по которому минимизируется сумма квадратов отклонений эмпирических значений от теоретических значений, т.е. найденных по уравнению регрессии:

Находя частные производные по а и b, приравнивая их к нулю, получаем систему уравнений, которую называют системой нормальных уравнений метода наименьших квадратов для прямой:
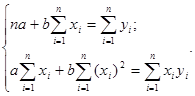
Решая эту систему, определяем значения переменных a и b.
Однако, определить параметры линейного уравнения регрессии можно другим способом:
Если разделить первое уравнение на n, то получим 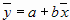 , где
, где 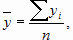
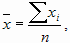 отсюда получаем:
отсюда получаем: 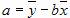 .
.
Подставив это выражение во второе уравнение системы, получим формулу для определения параметра b уравнения регрессии.
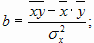
где 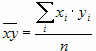 ,
, 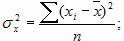 .
.
Коэффициент регрессии b показывает на сколько единиц в среднем изменяется переменная у при изменении переменной х на одну единицу.
Постоянная a дает значение зависимой переменной при нулевом значении х.
Возвращаясь к примеру зависимости прибыли предприятия от выработки продукции, обработаем статистические данные с помощью компьютерное программы «EconometricViews». Результаты представлены в следующей таблице:
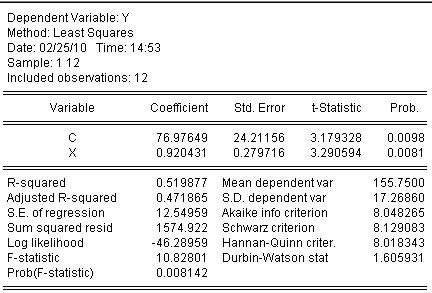
Таким образом, уравнение парной линейной регрессии зависимости прибыли предприятия от выработки продукции на одного человека имеет вид
у=76,98+0,92х.
На основании коэффициента регрессии перед переменной х, можно заключить следующие, если выработка продукции увеличится на 1 единицу на человека, можно ожидать увеличение прибыли предприятия на 0,92 тыс. тг.
3.Коэффициент корреляции.
Теснота парной линейной корреляционной связи измеряется коэффициентом корреляцииrxy:
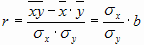
|r| 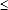 1.
1.
Чем ближе r к ±1, тем связь между показателями теснее. Если r близко к 0, то зависимость практически отсутствует, но имеется в виду отсутствие линейной зависимости.
Но при вычислении коэффициента корреляции и нахождении коэффициентов уравнения регрессии используются данные, имеющие случайные характер. Поэтому возникает вопрос о случайности связи между двумя величинами, установленной на основе таких данных. Для проверки связи двумя переменными используют корреляционную поправку:

где r - коэффициент корреляции, а n - объем выборки.
Если связь между Х и У существенная, то

С помощью уравнения регрессии можно найти выровненные значения показателя 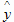 и вычислить отклонения
и вычислить отклонения 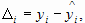 сумма которых всегда равна нулю. В качестве показателей погрешности выравнивания могут быть абсолютная величина среднего отклонения
сумма которых всегда равна нулю. В качестве показателей погрешности выравнивания могут быть абсолютная величина среднего отклонения
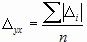
или средний квадрат отклонений (остаточная дисперсия у при выравнивании по х)
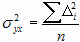 .
.
Для нашего примера: коэффициент детерминации 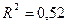 показывает, что 52% вариации прибыли связано с вариацией выработки продукции на одного работника. Величина коэффициента корреляции
показывает, что 52% вариации прибыли связано с вариацией выработки продукции на одного работника. Величина коэффициента корреляции  означает достаточно тесную связь рассматриваемых признаков.
означает достаточно тесную связь рассматриваемых признаков.
Рассмотрим еще один пример нахождения парной линейной корреляционной зависимости между урожайностью (ц/га) и количеством внесенных удобрений (кг/га) в 10 хозяйствах. Статистическую обработку выборочных данных осуществим с помощью ППП «Excel».