Примеры
а) Вычислить площадь фигуры, ограниченной линиями 
Решение.
Первый и важнейший момент решения – построение чертежа.
Выполним чертеж:
- уравнение y=0 задает ось «иксов»;
- х=-2 и х=1 – прямые, параллельные оси Оу;
- у=х2+2 – парабола, ветви которой направлены вверх, с вершиной в точке (0;2).
Замечание.Для построения параболы достаточно найти точки ее пересечения с координатными осями, т.е. положив х=0 найти пересечение с осью Оуи решив соответствующее квадратное уравнение, найти пересечение с осью Ох. Вершину параболы можно найти по формулам: 
Можно построить линии и поточечно.

На отрезке [-2;1] график функции y=x2+2 расположен над осьюOx, поэтому:

Ответ: S=9 кв.ед.
После того, как задание выполнено, всегда полезно взглянуть на чертеж и прикинуть, реальный ли получился ответ. В данном случае «на глазок» подсчитываем количество клеточек в чертеже – ну, примерно 9 наберётся, похоже на правду. Совершенно понятно, что если бы у нас получился, скажем, ответ: 20 квадратных единиц, то, очевидно, что где-то допущена ошибка – в рассматриваемую фигуру 20 клеточек явно не вмещается, от силы десяток. Если ответ получился отрицательным, то задание тоже решено некорректно.
Что делать, если криволинейная трапеция расположена под осью Ох?
b) Вычислить площадь фигуры, ограниченной линиями y=-ex, x=1 и координатными осями.
 Решение.
Решение.
Выполним чертеж.
Если криволинейная трапеция полностью расположена под осью Ох, то её площадь можно найти по формуле:

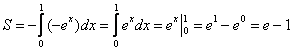
Ответ: S=(e-1) кв.ед.»1,72 кв.ед.
Внимание! Не следует путать два типа задач:
1) Если Вам предложено решить просто определенный интеграл без всякого геометрического смысла, то он может быть отрицательным.
2) Если Вам предложено найти площадь фигуры с помощью определенного интеграла, то площадь всегда положительна! Именно поэтому в только что рассмотренной формуле фигурирует минус.
На практике чаще всего фигура расположена и в верхней и в нижней полуплоскости.
с) Найти площадь плоской фигуры, ограниченной линиями у=2х-х2, у=-х.
Решение.
Сначала нужно выполнить чертеж. Вообще говоря, при построении чертежа в задачах на площадь нас больше всего интересуют точки пересечения линий. Найдем точки пересечения параболы 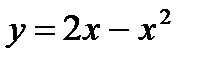 и прямой
и прямой  Это можно сделать двумя способами. Первый способ – аналитический. Решаем уравнение:
Это можно сделать двумя способами. Первый способ – аналитический. Решаем уравнение:

Значит, нижний предел интегрирования а=0 , верхний предел интегрирования b=3.
Строим заданные линии:
1.Парабола – вершина в точке (1;1); пересечение с осью Ох – точки(0;0) и (0;2).
2.Прямая – биссектриса 2-го и 4-го координатных углов.
А теперь Внимание!
Если на отрезке [a;b] некоторая непрерывная функция f(x) больше либо равна некоторой непрерывной функции g(x) , то площадь соответствующей фигуры можно найти по формуле:  .
И не важно, где расположена фигура – над осью или под осью, а важно,какой графикВЫШЕ(относительно другого графика), а какой– НИЖЕ.
В рассматриваемом примере очевидно, что на отрезке .
И не важно, где расположена фигура – над осью или под осью, а важно,какой графикВЫШЕ(относительно другого графика), а какой– НИЖЕ.
В рассматриваемом примере очевидно, что на отрезке  парабола располагается выше прямой, а поэтому из парабола располагается выше прямой, а поэтому из  необходимо вычесть необходимо вычесть 
|

Искомая фигура ограничена параболой сверху и прямой снизу.
На отрезке [0;3]  , по соответствующей формуле:
, по соответствующей формуле: 
Ответ: S=4,5 кв.ед.