Б. Изолированные особые точки

Определение. Особая точка 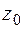функции называется изолированной, если в некоторой окрестности этой точки – аналитическая функция (то есть аналитическая в кольце ).

Классификация изолированных особых точек функции связана с поведением этой функции в окрестности особой точки.

Определение.Точка называется устранимой особой точкой функции , если существует конечный предел этой функции при .

Пример 5. Показать, что функция имеет в точке устранимую особенность.

Решение. Вспоминая первый замечательный предел, вычислим

Значит, в точке заданная функция имеет устранимую особенность. ☻

Задача 4. Показать, что точка устранимая для .

Определение.Точка называется полюсом функции , если эта функция неограниченно возрастает при , то есть .

Обратим внимание на связь между понятиями нуля и полюса аналитической функции. Представим функцию в виде .

Если точка является простым нулем функции , то функция имеет в простой полюс

Если точка – нуль порядка для функции , то для функции это полюс порядка .

Пример 6. Показать, что функция имеет в точке полюс третьего порядка.

Решение. Полагая , получим . При стремлении к нулю по любому закону имеем . Тогда , а с ним и сама функция неограниченно возрастает. Следовательно, , то есть особая точка является полюсом. Для функции эта точка, очевидно, является трехкратным нулем. Значит, для данной функции точка является полюсом третьего порядка. ☻

Задача 5. Показать, что в точке имеет простой полюс.

Определение.Точка 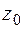называется существенно особой точкой функции , если в этой точке не существует ни конечного, ни бесконечного предела функции (поведение функции не определено).

Пусть является существенно особой точкой функции . Тогда для любого наперед заданного комплексного числа найдется такая последовательность точек , сходящаяся к , вдоль которой значения стремятся к : (теорема Сохоцкого).

Пример 7. Показать, что функция в точке имеет существенную особенность.

Решение. Рассмотрим поведение заданной функции в окрестности точки . При вдоль положительной части действительной оси (т.е. ) имеем и ; если же вдоль отрицательной части действительной оси (т.е. ), то и . Значит, не существует предела при . По определению, в точке функция имеет существенную особенность.

Рассмотрим поведение функции в нуле с точки зрения теоремы Сохоцкого. Пусть – любое комплексное число, отличное от нуля и бесконечности.

Из равенства находим . Полагая , получим последовательность точек , . Очевидно, . В каждой точке этой последовательности функция равна , поэтому и

. ☻

Задача 6. Показать, что функция имеет в точке существенную особенность.

Бесконечно удаленная точка всегда считается особой для функции . Точка называется изолированной особой точкой функции , если эта функция вне некоторого круга с центром в начале координат не имеет других особых точек.

Классификацию изолированных особых точек можно распространить и на случай .

Пример 8. Показать, что функция имеет на бесконечности двукратный полюс.

Решение. Рассмотрим функцию , где – аналитическая функция в окрестности точки , причем . Значит, функция имеет на бесконечности двукратный нуль, но тогда для функции точка является двукратным полюсом. ☻

Пример 9. Показать, что функция имеет на бесконечности существенную особенность.

Решение. Аналогичная задача рассмотрена в пр.7. Рассмотрим поведение функции в окрестности бесконечно удаленной точки. При вдоль положительной части действительной оси , а при вдоль отрицательной части действительной оси . Значит, не существует предела функции в точке и в силу определения эта точка – существенно особая. ☻

О характере особенности функции в точке можно судить по главной части лорановского разложения в окрестности этой точки.

Теорема 1.Для того чтобы точка была устранимой особой точкой функции , необходимо и достаточно, чтобы соответствующее лорановское разложение не содержало главной части.

Задача 6. Пользуясь тейлоровским разложением функции в окрестности точки , показать, что имеет в нуле устранимую особенность.

Теорема 2.Для того чтобы точка была полюсом функции , необходимо и достаточно, чтобы главная часть соответствующего лорановского разложения содержала конечное число членов:

.

Номер старшего отрицательного члена определяет порядок полюса.

В этом случае функцию можно представить в виде

, (8)

где - аналитическая в точке функция, , – порядок полюса.

Пример 10. Показать, что функция имеет в точках и простые полюсы.

Решение. Рассмотрим точку . Воспользуемся лорановским разложением данной функции в окрестности этой точки, полученным в примере 2:

Так как в главной части этого разложения старшая (и единственная) отрицательная степень равна единице, то точка – простой полюс данной функции.

Можно было получить этот результат другим путем. Представим в виде и положим – это функция, аналитическая в точке и . Значит, и в силу (8) в точке данная функция имеет простой полюс.

Еще один способ: рассмотрим функцию , которая в точке имеет простой нуль. Значит, в этой точке имеет простой полюс.

Аналогично, если записать функцию в виде , где – функция, аналитическая в точке и , то сразу ясно, что точка – простой полюс функции . ☻

Задача 7. Показать, что функция имеет полюс 2 –го порядка в точке и полюс 4 –го порядка в точке .

Теорема 3.Для того чтобы точка была существенно особой точкой функции , необходимо и достаточно, чтобы главная часть лорановского разложения в окрестности точки 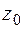содержала бесконечное число членов.

Пример 11. Определить характер особенности в точке функции

Решение. В известном разложении косинуса положим вместо :

Значит, лорановское разложение в окрестности точки имеет вид

Здесь правильная часть – одно слагаемое . А главная часть содержит бесконечное число слагаемых, поэтому точка – существенно особая. ☻

Задача 8. Показать, что в точке функция имеет существенную особенность.

Рассмотрим некоторую функцию и запишем ее лорановское разложение в точке :

.

Произведем замену , при этом точка переходит в точку . Теперь в окрестности бесконечно удаленной точки имеем

.

Осталось ввести новое обозначение . Получаем

,

где – главная часть, а – правильная часть лорановского разложения функции в окрестности бесконечно удаленной точки. Таким образом, в лорановском разложении функции в окрестности точки главная часть – это ряд по положительным степеням , а правильная часть – ряд по отрицательным степеням. С учетом этого заме

чания приведенные критерии для определения характера особенности остаются в силе и для бесконечно удаленной точки.

Пример 12. Выяснить характер особенности функции в точке .

Решение. Положим , тогда . Рассмотрим функцию , аналитическую в точке . Запишем несколько первых членов тейлоровского разложения функции в окрестности нуля. Вычислим

,

,

.

Значит, .

Осталось произвести обратную замену :

Получили разложение функции в окрестности бесконечно удаленной точки. Так как существует конечный предел , то в точке функция имеет устранимую особенность. ☻

Пример 13. Показать, что имеет в нуле двукратный полюс, а на бесконечности – простой полюс.

Решение. Запишем функцию в виде суммы: . В окрестности нуля первое слагаемое – это правильная часть лорановского разложения, второе слагаемое – главная часть лорановского разложения этой функции. Так как старшая отрицательная степень равна 2, то в нуле полюс двукратный. В окрестности бесконечно удаленной точки правильная и главная части меняются местами, теперь – это главная часть лорановского разложения. Так как старшая положительная степень равна единице, то в бесконечно удаленной точке функция имеет простой полюс. ☻

Задача 9. Выяснить характер особенности функции в бесконечно удаленной точке. Ответ: существенная особенность.

Задача 10. Выяснить характер особенности в точке . Ответ: полюс 2 –го порядка.

Задача 11. С помощью лорановского разложения в окрестности бесконечно удаленной точки выяснить характер особенности функции в этой точке. Ответ: существенная особенность.

Замечание 1. Здесь рассматривались только изолированные особые точки.

Замечание 2. В случае, когда функция имеет в существенную особенность, для функции особая точка может оказаться неизолированной.

Пример 14.Функция в точке имеет существенную особенность. Показать, что для функции не является изолированной особой точкой.

Решение. Функция имеет полюсы в точках , которые найдем как нули знаменателя из уравнения . Очевидно, , то есть полюсы накапливаются к началу координат. Значит, в любой сколь угодно малой окрестности точки имеются полюсы, отличные от . Особая точка не является изолированной – это предельная точка полюсов данной функции. ☻

Пример 15.Функция в бесконечно удаленной точке имеет существенную особенность. Показать, что точка для функции не является изолированной особой точкой.

Решение. Функция имеет бесчисленное множество полюсов в нулях знаменателя, то есть в точках , . Так как , то точка , в любой окрестности которой имеются полюсы , является предельной для полюсов.